Hochpass, Tiefpass - acid

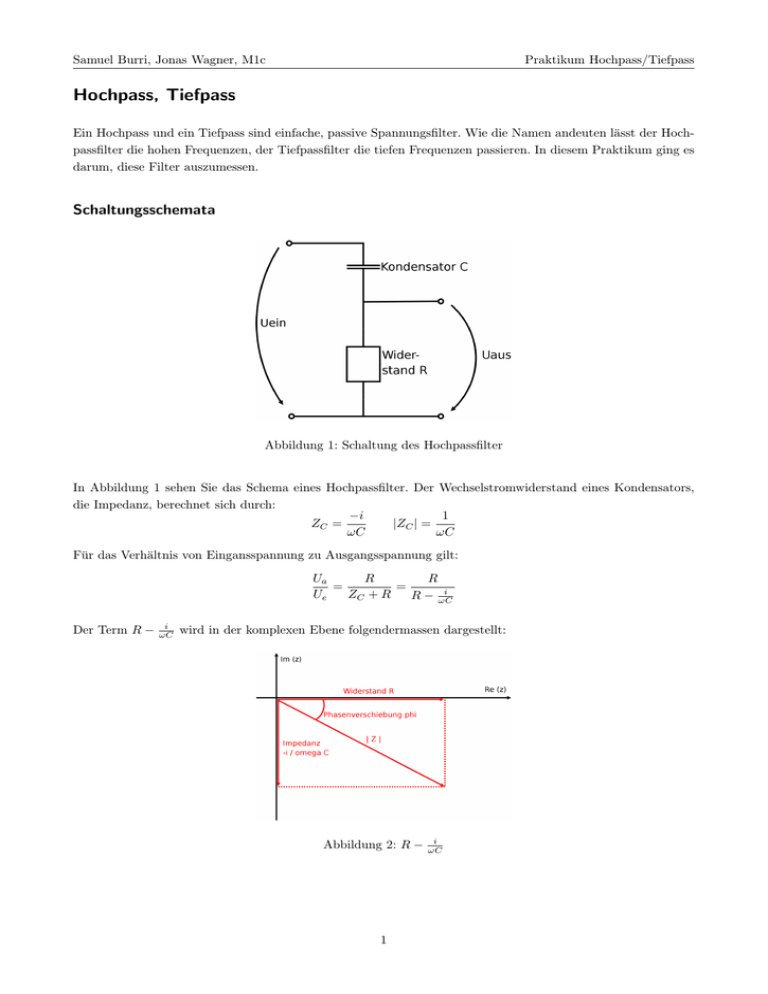
Samuel Burri, Jonas Wagner, M1c
Praktikum Hochpass/Tiefpass
Hochpass, Tiefpass
Ein Hochpass und ein Tiefpass sind einfache, passive Spannungsfilter. Wie die Namen andeuten lässt der Hochpassfilter die hohen Frequenzen, der Tiefpassfilter die tiefen Frequenzen passieren. In diesem Praktikum ging es
darum, diese Filter auszumessen.
Schaltungsschemata
Abbildung 1: Schaltung des Hochpassfilter
In Abbildung 1 sehen Sie das Schema eines Hochpassfilter. Der Wechselstromwiderstand eines Kondensators,
die Impedanz, berechnet sich durch:
−i
1
ZC =
|ZC | =
ωC
ωC
Für das Verhältnis von Eingansspannung zu Ausgangsspannung gilt:
R
Ua
R
=
=
i
Ue
ZC + R
R − ωC
Der Term R −
i
ωC
wird in der komplexen Ebene folgendermassen dargestellt:
Abbildung 2: R −
1
i
ωC
Samuel Burri, Jonas Wagner, M1c
Praktikum Hochpass/Tiefpass
ϕ steht dabei für die Phasenverschiebung und Z für den Betrag. Es folgt also:
Ua R
R
1
=
tan ϕ =
Ue Z = q 2
ωCR
R + 1
ω2 C 2
Abbildung 3: Schaltung des Tiefpassfilter
Abbildung 3 zeigt das Schaltschema eines Tiefpassfilter. Im Vergleich zum Hochpass wurden der Widerstand
und der Kondensator vertauscht.
Für das Verhältnis von Eingansspannung zu Ausgangsspannung gilt hier:
i
− ωC
1
Ua
ZC
1
= RωC
=
=
=
i
Ue
R + ZC
1 + iRωC
R − ωC
− i +1
Der Term 1 + iRωC wird in der komplexen Ebene folgendermassen dargestellt:
Abbildung 4: 1 + iRωC
Es folgt also:
Ua 1
= p
Ue 1 + (RωC)2
tan ϕ =
RωC
1
Versuchsaufbau
Die Schaltung für den Hochpass wurde aufgebaut. Die Eingangsspannung wurde von einem Funktionsgenerator
erzeugt. Auf einem KO wurde dann die Ausgangsspannung mit der Eingangsspannung verglichen. Folgende
Werte wurden gemessen:
2
Samuel Burri, Jonas Wagner, M1c
Praktikum Hochpass/Tiefpass
f (kHz)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
50
100
500
1000
2500
Ua (V)
0.10
0.21
0.32
0.40
0.50
0.65
0.72
0.81
0.88
1.00
1.05
1.20
1.25
1.35
1.40
1.48
1.60
1.62
1.64
1.80
1.81
1.89
1.93
2.00
2.05
2.10
2.12
2.20
2.21
2.29
2.33
2.38
2.40
2.47
2.50
2.53
2.59
2.60
2.60
2.62
2.90
3.24
3.40
3.45
3.55
3
ϕ (Grad)
90.00
70.00
55
53
44
45
36
37
15.84
9.2
0
0
Samuel Burri, Jonas Wagner, M1c
Praktikum Hochpass/Tiefpass
Für das Verhältnis von Eingangsspannung zu Ausgangsspannung in Abhängigkeit der Frequenz wurde ein Diagramm erstellt. Sie finden dieses Diagramm auf Seite 4. Die gemessenen Werte lagen allesamt etwas zu tief was
wahrscheinlich auf fehlerhaftes Ablesen am KO zurückzuführen ist. Es wurde ein Widerstand von 10kOhm und
ein Kondensator von 470nF verwendet.
Auch die Phasenverschiebung in Abhängigkeit von der Frequenz wurde grafisch dargestellt. Hier stimmen die
vorhandenen Werte sehr gut mit der theoretischen Kurve überein. Dieses Diagramm finden Sie auf Seite 5.
Quellen
Die Formeln und theoretischen Grundlagen stammen aus folgenden Werken:
• orell füssli: Formeln und Tafeln, 9. Auflage (2001)
• H.J. Wiehl: Elektromagnetismus-Skript, 1999
Abbildung 5: Das Verhältnis der Spannungen in Abhängigkeit von der Kreisfrequenz der Spannung
4
Samuel Burri, Jonas Wagner, M1c
Praktikum Hochpass/Tiefpass
Abbildung 6: Die Phasenverschiebung als Funktion von der Kreisfrequenz der Spannung
5