3. Versuch 3 (Thermische Widerstände)

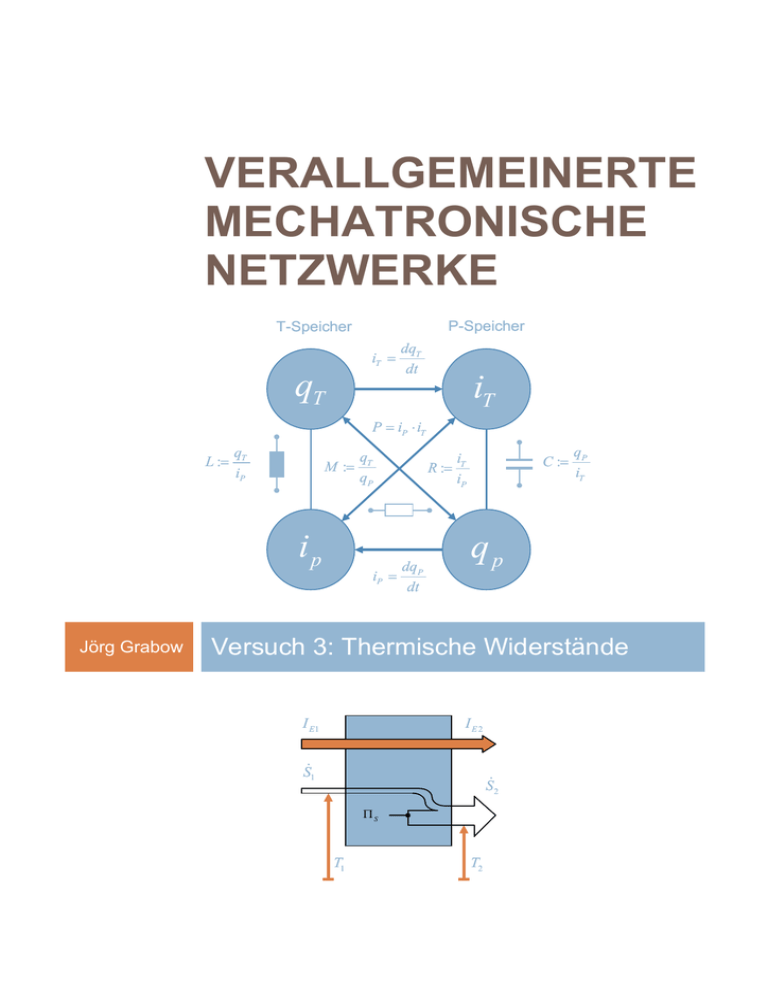
VERALLGEMEINERTE
MECHATRONISCHE
NETZWERKE
P-Speicher
T-Speicher
iT =
qT
dqT
dt
iT
P = iP ⋅ iT
L :=
qT
iP
M :=
ip
Jörg Grabow
qT
qP
dq
iP = P
dt
C :=
i
R := T
iP
qP
iT
qp
Versuch 3: Thermische Widerstände
I E1
IE2
Sɺ1
Sɺ2
ΠS
T1
T2
Verallgemeinerte Mechatronische Netzwerke
1.Thermische Widerstände
REZIPROKE WANDLER | ZWEITORE
1.1 EINLEITUNG
Der Begriff des thermischen Widerstandes fährt in der Technik immer wieder zu Fehlinterpretationen. Sei es bei Problemen der Wärmeleitung oder der Konvektion, immer wird an dieser Stelle mit
dem thermischen Widerstand operiert. Die Missverständnisse die dabei auftreten, sind vergleichbar mit dem Begriff des Strömungswiderstandes. Leider hat sich hier historisch eine sprachliche
Unsicherheit eingeschlichen. Ursprünglich war dem Begriff des Widerstandes der enge Zusammenhang zwischen einer Flussgröße und der damit verbundenen reibungsbehafteten Energiedissipation zugeordnet. Das bedeutet, dass ein Widerstand in jeden Fall eine Quelle von Wärme ist.
Schon
allein
die
herkömmliche
Definition
des
thermischen
Widerstandes
als Rth =
∆T
;
Q
[ Rth ] =
K
; P = RthQ 2 ;
W
[ P ] = K ⋅ W!
zeigt, dass über den so definierten Wider-
stand keine Leistung ab fallen kann. Die korrekte Leistungsformulierung im Sinne der mechatronischen Netzwerke ist jedoch die unbedingte Voraussetzung für die Kopplung der physikalischen
Teilsysteme untereinander. Basiert doch die Kopplung gerade auf dem Austausch der Prozessleistung.
1.2 AUSGANGSSCHALTUNG
Zur Verdeutlichung der Phänomene des thermischen Widerstandes betrachten wir die Außenwand
eines Gebäudes (Abb. 1.1).
I E1 = I E 2
IE
I E1
T1
T2
IE2
Sɺ1
Sɺ2
ΠS
λW ; A
d
T1
T2
Abb.1.1: Gebäudewand als thermischer Widerstand
Wir interessieren uns dabei für den thermischen Widerstand der Wand, die Entropieproduktionsrate sowie die erzeugte Prozessleistung der Wand selber. Um ein entsprechendes Simulationsmodell aufzubauen sei zunächst das thermische Ersatzschaltbild der Wand untersucht (Abb.1.2).
Rev. 1.1
Seite 1
Verallgemeinerte Mechatronische Netzwerke
I E1
Sɺ1
∆T
RT
Sɺ2
T1
!
∆I E = 0
T2
IE2
Abb.1.2: thermisches Ersatzschaltbild der Wand
Die im Flusskreislauf fließenden Energieströme können formal über die Flüsse und ihre jeweiligen
Potentiale ausgedrückt werden.
I E1 = Sɺ1 ⋅ T1 = Qɺ1
I = Sɺ ⋅ T = Qɺ
E2
2
2
2
Der Energieerhaltungssatz sagt uns, dass beide Energieströme jedoch gleich sein müssen
( I E1 = I E 2 ) . Damit ergeben sich Zwangsläufig zwei unter schiedliche Entropieströme.
1.3 VERSUCHSDURCHFÜHRUNG
Für das thermische System Wand ist unter Vernachlässigung der thermischen Kapazität eine äquivalente Simulationsschaltung mittels LTSpice zu entwerfen. Für das Modell der thermischen Wand
seien dazu die folgenden Parameter gegeben.
Thermische Wand
Nr.
Kenngröße
Parameter
1
Wandfläche
A = 7.5 ⋅ m 2
2
Wanddicke
d = 0.3 ⋅ m
3
Wärmestrom
Qɺ = 41 W
4
Außentemperatur
T2 = 5 °C
5
Wärmeleitzahl
λW = 0.11 ⋅
Rev. 1.1
W
mK
Seite 2
Verallgemeinerte Mechatronische Netzwerke
2. AUFGABENSTELLUNG
2.1 Vorbereitung
•
Wie ist der thermische Widerstand für mechatronische Netzwerke definiert? Wodurch
unterscheidet er sich in der orthodoxen Form des thermischen Widerstandes?
•
Da das Simulationssystem LTSpice bei elektrischen Widerständen einen konstanten
Stromfluss voraussetzt, kann dieser Widerstand für die thermische Simulation so nicht verwendet werden. Wie muss die Widerstandsdefinition erweitert werden?
2.2 Versuchsdurchführung
•
Erstellen Sie das thermische Ersatzschaltbild der Aufgabenstellung nach Abb. 1.1. Definieren Sie sich dazu ein neues Bauelement als thermischen Widerstand.
•
Berechnen Sie die Größe des thermischen Widerstandes, die dissipative Leistung über
diesem Widerstand, die Entropieproduktionsrate, die Entropieströme sowie die sich einstellende Innentemperatur T1 .
•
Ordnen Sie Ihren neu definierten Bauelementen die berechneten Parameter zu und
führen Sie die Simulation mittels LTSpice durch.
LITERATUR
[1] Ballas,R.G.; Pfeifer,G.; Werthschützky,R..: Elektromechanische Systeme in der Mikrotechnik
und Mechatronik, Springer Verlag Berlin Heidelberg 2000,2009
[2]
Janschek,K.: Systementwurf mechatronischer Systeme, Springer Verlag Berlin Heidelberg
2010
[3]
Grabow,J.: Verallgemeinerte Mechatronische Netzwerke, Oldenbourg Verlag 2013
Rev. 1.1
Seite 3