Ein Sweepline-Algorithmus für Voronoi

Ein Sweepline-Algorithmus für Voronoi-Diagramme
Dimitrios Skouras
21. Januar 2008
Inhaltsverzeichnis
1 Einleitung
1
2 Punkt-Sites
2.1 Allgemeines . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.2 Die Transformation ∗ . . . . . . . . . . . . . . . . . . . . . . .
2.3 Der Algorithmus für V und V ∗ . . . . . . . . . . . . . . . . .
2
2
2
4
3 Linien-Segment-Sites
3.1 Allgemeines . . . . . . . . . . . . . . . . . . . . .
3.2 Das Voronoi-Diagramm für Linien-Segment-Sites
3.3 Die Transformation ∗ . . . . . . . . . . . . . . . .
3.4 Der Algorithmus für V ∗ und V . . . . . . . . . .
7
7
7
8
9
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
4 Gewichtete Punkt-Sites
11
5 Schlussfolgerung
11
I
1
Einleitung
Das Ziel des Sweepline-Algorithmus ist es, aus einer gegebenen Menge von
Sites, das dazu passende Voronoi-Diagramm (im Folgenden VD) zu bestimmen. Die Sites können Punkte, Linien, oder gewichtete Punkte sein
und liegen im Normalfall in ihrer Voronoi-Region (im Folgenden VR). Der
Sweepline-Algorithmus lässt eine horizontale Linie von unten nach oben
durch die Ebene wandern und speichert die Schnitte in der dafür vorgesehenen Datenstruktur. Dadurch werden die VR vor den Sites erfasst, was
eine grosse Schwierigkeit darstellt.
Steven Fortune überwandt diese, indem er eine geometrische Transformation auf das eigentliche VD anwandt.
Die Transformation ∗ bildet jede Site auf sich selbst ab und ist dann unterster Punkt der transformierten VR. Dies wird durch die Tatsache gewährleistet, dass jeder Punkt z ∈ V D auf den obersten Punkt des Voronoi-Kreises
um z transformiert wird. Dabei ist der Radius des Kreises definiert durch
den kleinsten euklidischen Abstand zur nächsten Site p. Dank ∗ muss die
VR erst betrachtet werden, wenn eine Site von der Sweepline geschnitten
wird.
Die Rücktransformation zum eigentlichen VD ist einfach und wird gleich
mit berechnet. Somit braucht der Algorithmus nur die untransformierten
Kanten und Knoten zu speichern.
Der Sweepline-Algorithmus hat für alle Fälle (Punkt-Sites, Linien-SegmentSites und gewichtete Punkt-Sites) eine Laufzeit von O(n log(n)) und einen
Speicherplatzbedarf von O(n). Dabei bildet der Algorithmus für die PunktSites den Standard-Algorithmus, der dann für die anderen Fälle modifiziert
wird.
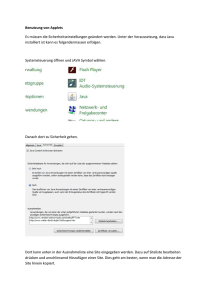
Abbildung 1: Sweeprichtung für V und V ∗
1
2
2.1
Punkt-Sites
Allgemeines
Wir betrachten nun den einfachen Fall von Punkten in der euklidischen
Ebene. Für die folgenden Betrachtungen sei S die gegebene Menge aller
Sites. Wenn p ∈ R2 , dann ist px die x-Koordinate und py die y-Koordinate
und p lexikographisch kleiner“ q bedeutet, dass py < qy oder py = qy und
”
px < qx .
Definition 2.1.1. Für p ∈ S und z ∈ R2 sei dp : R2 −→ R die euklidische
Distanz von z zu p.
Definition 2.1.2. Für z ∈ R2 sei d : R2 −→R; d(z) = |{z}
min dp sei die euklip∈S
dische Distanz zur nächsten Site
Definition 2.1.3. Bisektor Bpq = z ∈ R2 |dp (z) = dq (z) , ∀p, q ∈ S
Definition 2.1.4. Halbebene Rpq = z ∈ R2 |dp (z) ≤ dq (z) , ∀p, q ∈ S
\
Definition 2.1.5. Voronoi-Region Rp =
Rpq ; ∀p, q ∈ S
|{z}
p6=q
Die Voronoi-Region Rp ist konvex und kann am Rand von V unbegrenzt
sein. Das Voronoi-Diagramm V(S), oder auch einfach nur V, besteht aus
allen Grenzen, die zwischen zwei Sites liegen. Die genaue Definition lautet:
Definition 2.1.6. Voronoi-Diagramm V (S) = z ∈ R2 |∃p6=q : d(z) = dp (z)
= dq (z) , ∀p, q ∈ S
Ein Knoten v ∈ V ist ein Punkt, der zu 3 Sites den gleichen Abstand
hat. Eine Kante epq ∈ V ist ein Stück der Grenze der VR und liegt zwischen
den Sites p und q. Allgemein sind Kanten durch zwei Endpunkte begrenzt,
oder sie haben genau einen Endpunkt und bilden eine zu einer Seite offene
Halblinie, die zwischen zwei Sites liegt.
Bemerkung 2.1.7. Es gibt höchstens O(n) Knoten und Kanten
2.2
Die Transformation ∗
Die Abbildung ∗ wird definiert durch ∗(z) := (x, y + d(z)) und bildet den
Punkt z ∈ R2 auf den höchsten Punkt des Voronoi-Kreises um z ab. Die
Transformation ist stetig durch ihre Eigenschaften wird gewährleisetet, dass
alle Punkte der Voronoi-Region um eine Site p, im transformierten VoronoiDiagramm VD* über p liegen und somit p das Minimum der Region darstellt.
Offensichtlich werden Sites und vertikale Linien auf sich selbst abgebildet.
Angewandt auf den Sweepline-Algorithmus bedeutet dies, dass die Sweepline
eine Site als ersten Teil der gesamten Region schneidet.
2
Notation 2.2.1. Für einen transformierten Bisektor ∗(Bpq ) schreiben wir
∗
auch Bpq
Zur Untersuchung von ∗, betrachten wir zunächst die Hilfstransformation
∗p , welche ähnlich wie ∗ definiert ist, jedoch die Grenzen in Abhängigkeit zu
einer festen Site p transformiert. Also sind die beiden Transformationen auf
einer festen Region Rp identisch. Es gilt ∗p (z) := (x, y + dp (z)).
Lemma 2.2.2. .
• Wenn py > qy ⇒ ∗(Bpq ) ist eine Hyperbel, die nach oben offen ist und
ihr Minimum in p hat.
• Wenn py = qy ⇒ ∗(Bpq ) ist eine vertikale Gerade über (r, y + dp (r, y))
x
mit r = px +q
2 .
Sei nun epq eine Kante von V, dann ist e∗pq ein Stück einer Hyperbel,
oder einer vertikalen Linie.
Lemma 2.2.3. Sei v ∈ V ein Knoten und v ∗ ∈ V ∗ , der höchste Punktt
des Voronoi-Kreises um v. Seien p, s ∈ S die Sites, welche man als erste
erreicht, wenn man von v ∗ ) aus, nach links bzw. rechts auf dem Kreis wandert. Dann
1. v ∗ ist Site ⇒ genau zwei Kanten e∗pv und e∗vq verlaufen von v ∗ aus
nach oben und die restlichen nach unten.
2. v ∗ ist keine Site ⇒ genau eine Kante e∗pq verläuft von v ∗ aus nach
oben und die restlichen nach unten.
Mit Hilfe der Lemmata und der vorausgegangenen Beobachtungen können
wir nun jeden Punkt x im Bildbereich von ∗ klassifizieren. Die folgenden
Fälle schliessen sich gegenseitig aus:
• x liegt im innener eine Region Rp∗ .
• x liegt auf einer Kante e∗pq , ist aber weder eine Site noch ein Knoten
in V ∗ .
• x ist eine Site und kein Knoten. Dann ist der Punkt das Minimum der
Region Rp∗ und der Kante e∗xq , für ein p ∈ S.
• x ist ein Knoten und keine Site. Dann veräuft von dem Punkt aus
genau eine Kante nach oben und mindestens zwei nach unten.
• x ist Site und Knoten. Dann verlaufen von diesem Punkt genau zwei
Kanten nach oben und mindestens eine nach unten.
3
2.3
Der Algorithmus für V und V ∗
Ein Sweepline-Algorithmus genügt, um V ∗ zu berechnen. Bildlich bewegt
sich eine horizontale Linie von unten nach oben durch die Ebene. Man erhält
die Regionen und die Kanten durch den Schnitt mit der Sweepline und
speichert diese in der Datenstruktur. Eine Region wird das erste Mal in der
zugehörigen Site getroffen und verlassen, wenn sich zwei Kanten schneiden.
Die Haltepunkte der Sweepline sind die Sites und die Knoten.
Die Koordinaten der Sites sind gegeben und die Koordinaten der Schnittpunkte werden vom Algorithmus berechnet, indem er jedes mal wenn eine
neue Kante getroffen wird, den Schnittpunkt mit dieser und mit ihren Nachbarkanten berechnet.
Wir bezeichnen den Sweepline-Algorithmus von Punkt-Sites im Folgenden mit Algorithmus1. Er speichert das Voronoi-Diagramm V ∗ als eine Liste
von Bisektoren, zu denen zwei Knoten gegeben sind, welche die beiden Endpunkte der korrespondierenden Kante sind. Wenn ein Bisektor nur durch
einen Knoten gegeben ist, ist die korrespondierende Kante eine Halbgerade,
die zu einer Seite unbegrenzt ist.
Wir gehen beim Algorithmus von der Tatsache aus, dass immer eine eindeutige, unterste Site in unserer Datenstruktur existiert. Andernfalls mdie
Zeilen 2 und 3 von Algorithmus1 umgeschrieben werden.
Wenn diese Annahme nun gegeben ist und bei zwei benachbarten Regionen Rp und Rq gilt, dass py < qy , dann ist ∗p (Bpq ) eine nach oben geöffnete
Hyperbel,die die Site p als Minimum hat.
Notation 2.3.1. Den Teil der Hyperbel, der links von p verläuft (monoton
− . Den Teil der Hyperbel, der rechts von p
fallender Teil) nennen wir Cpq
+.
verläuft (monoton steigender Teil) nennen wir Cpq
+ und C − sind beides Grenzen und von einer festen horizontalen Linie
Cpq
pq
+ eine senkrechte
nur einmal geschnitten. Wenn py = qy , ist ∗p (Bpq ) = Cpq
−
Halblinie und folglich müssen wir Cpq = ∅ setzen. Schreibe Cpq , wenn die
Wahl unwichtig ist.
In Zeile 8 von Algorithmus1 wird eine Suche ausgeführt, welche die Region findet, die zu einer neu entdeckten Site gehhört. Sie kann als Binärsuche
auf einer Liste L implementiert werden, solange L die Regionen und Grenzen
geordnet von links nach rechts enthält.
4
Algorithmus1 :
• Die Eingabe ist eine Menge von n Sites mit eindeutigem untersten
Element.
• Die Ausgabe sind die Bisektoren und die Knoten von V ∗ .
• Die Datenstruktur Q ist eine P riority − Queue von Punkten in der
Ebene. Die lexikographisch sortierten Punkte enthalten jeweils eine
Site, oder einen Knoten. Q kann mehrere Ereignisse für den gleichen
Punkt enthalten. Die Reihenfolge dieser gleichzeitigen Ereignisse ist
unwichtig.
• Die Datenstruktur L speichert die aktuell von der Sweepline geschnittenen Regionen und Grenzen lexikographisch in eine Folge (r1 , c1 ,
r2 , c2 , · · · , rk , ck ) . Beachte, dass eine Region mehr als einmal
auftauchen kann.
1. inizialisiere Q mit allen Sites
2. p ← extractM in(Q)
3. L ← die Liste, die Rp enthält
4. while Q nicht leer begin
5. p ← extractM in(Q)
6. case
7. p ist Site:
8. finde ein Halteereignis einer Region Rq , die p enthält auf der Liste L
∗
9. erzeuge einen Bisektor Bpq
− , R∗ , C + , R∗ , ... anstatt R∗
10. verändere die Liste L so, dass sie ..., Rq∗ , Cpq
q
p
pq
q
enthält.
− und C + mit benachbarten Grenzen in
11. füge die Schnitte zwischen Cpq
pq
Q ein
12. p ist ein Schnitt:
13. Sei p der Schnitt von den Grenzen Cpr und Crs .
∗
14. erzeuge einen Bisektor Bqs
− oder C + geeignet enthält,
15. verändere die Liste L so, dass sie Cqs =Cqs
qs
anstelle von Cqr , Rr∗ , Crs .
5
16. lösche in Q alle Schnitte zwischen Cqs und ihren Nachbarn
17. füge alle Schnitte zwischen Cqs und ihren Nachbarn in Q ein
∗ , B∗ , B∗
18. markiere p als einen Knoten und als einen Endpunkt von Bqr
rs
qs
19. end
Theorem 2.3.2. Man kann Algorithmus1 so implementieren, dass er das
transformierte Voronoi-Diagramm mit einer Laufzeit von O(n log(n)) und
einem Speicherplatzbedarf von O(n) erstellt.
Beweis. Die while-Schleife wird O(n)-mal durchlaufen und erstellt dabei
O(n) Bisektoren. Q enthält maximal zwei Einträge je Grenze und einen pro
Site, also O(n). Da man Q als Heap implementieren kann, brauchen die verwendeten Operationen EIN F Ü GEN , LÖSCHEN und EXT RACT M IN
nur eine Laufzeit von O(log(n)). L enthält ebenfalls O(n) Einträge, weil ein
Bisektor nur einmal von einer horizontalen Linie geschnitten werden kann. L
kann man als AV L−Baum implementieren und bekommt für die benötigten
Operationen LÖSCHEN , EIN F Ü GEN und SU CHEN (in Zeile 10) eine
Laufzeit von O(log(n)). Folglich braucht man für den gesamten Algorithmus
eine Laufzeit von O(n log(n)).
Theorem 2.3.3. Nach leichten Modifikationen, kann Algorithmus1 sofort
das nicht-transformierte Voronoi-Diagramm mit einer Laufzeit von O(n log(n))
und einem Speicherplatzbedarf von O(n) ausgeben.
Beweis. Die Sites in V und V ∗ sind identisch und man bekommen die Kanten
auch hier, indem man die Bisektoren erzeugt und diese dann mit den Endpunkten der korrespondierenden Kanten markiert. Die Datenstrukturen und
Operationen bleiben bis auf kleine Unterschiede die Gleichen. Somit kann
dieser Algorithmus ebenfalls mit einer Laufzeit von O(n log(n)) implementiert werden.
6
3
Linien-Segment-Sites
3.1
Allgemeines
Der Algorithmus1 kann nach Modifikationen auch das Voronoi-Diagramm
von Linien-Segment-Sites berechnen. Die Idee ist die Gleiche, und somit
sind die Sites nach der Transformation die untersten Punkte ihrer Regionen. Natürlich wird der Algorithmus und das Voronoi-Diagramm dadurch
etwas komplexer. Leider verhält sich die Transformation nicht so schön.
Die Bisektoren zweier disjunkter Segmente bilden eine Kurve und können
aus bis zu sieben Bereichen bestehen. Jeder, ein Teil einer Geraden, oder
einer Hyperbel. Schlecht ist, dass der Bisektor zweier Segmente mit dem
gleichen Endpunkt nicht eindimensional sein muss, solange eine zweidimensioale Region existiert, für welche dieser Endpunkt, der näheste Punkt zu
beiden Sites darstellt.
Durch eine andere Definition des VD kann die Situation vereinfacht werden.
Wir brauchen, dass jedes Segment in drei Sites aufgeteilt werden kann. In
die beiden Endpunkte und das Liniensegment selbst. Dann unterscheiden
wir, ob die Endpunkte des Segments, oder das Segment selber näher sind.
Die Konsequenz ist, dass der Bisektor zwischen zwei Sites immer eine
Linie, oder eine Parabel darstellt.
3.2
Das Voronoi-Diagramm für Linien-Segment-Sites
Die Endpunkte einer Linien-Segment-Site werden wie Punkt-Sites behandelt. Ein Schnitt zweier Linien-Segment-Sites ist nur in den Endpunkten
möglich. Die Distanz eines Punktes z zu einer Site p (also dp (z)), wird definiert als die euklidische Distanz zwischen z und dem Punkt auf p, der am
nähesten zu z liegt. Wir definieren auch noch eine tangenziale Kontaktregion
tp , die im Falle einer Punkt-Site der R2 ist und bei einer Linien-Segment-Site
das Band, welches entsteht, wenn man die beiden Endpunkte der Site mit
je einer Geraden schneidet, die orthogonal zum Segment verläuft. Nun kann
man die Distanz d(z) analog zum vorherigen Abschnitt definieren, mit dem
Unterschied, dass z in tp liegen muss.
Für die Definitionen von Bisektoren, Voronoi-Regionen und des VoronoiDiagramms, müssen die relevanten Punkte ebenfalls in den tangenzialen
Kontaktregionen liegen.
Mögliche Formen von Bisektoren (für p, q ∈ S):
• p, q Punkte ⇒ Bpq ist eine Halbline zwischen den Punkten.
• p Endpunkt von Linien-Segment q ⇒ Bpq ist die Linie, die senkrecht
zu q und durch p geht.
7
• p Punkt und q ein nicht-inzidentes Linien-Segment ⇒ Bpq ist Bereich
einer Parabel.
• p innerer Punkt von Linien-Segment q ⇒ Bpq ist leer.
• p, q Linien-Segmente ⇒ Bpq ist:
– ein Punkt
– ein Segment
– leer, wenn tp ∩ tq = ∅
– wenn p und q co − linear mit gleichem Endpunkt, die senkrechte
Gerade durch diesen Endpunkt.
Die Voronoi-Region muss nicht konvex sein, es reicht wenn sie sternförmig
um die Site verläuft. D.h., dass jede Gerade, die einen beliebigen Punkt auf
der Site mit einem beliebigen Punkt in der Region verbindet, komplett in
der Voronoi-Region liegt und die Grenzen nicht schneidet. Knoten und Kanten werden analog zu Abschnitt 2 definiert, mit der Ausnahme, dass auch
hier ein Knoten in tp liegen muss. Die Kanten sind eindimensional.
3.3
Die Transformation ∗
Die Transformation bewirkt das Gleiche und ist fast identisch definiert, wie
die Transformation in Abschnitt 2. Sie ist überall 1 : 1, ausser bei vertikalen Segmenten unterhalb von p, bei denen alle Punkte auf p transformiert
werden.
Nun untersuchen wir die transformierten Bisektoren:
• p, q Punkte ⇒ ∗p (Bpq ) ist, wenn q:
– nicht horizontal, eine Hyperbel.
– horizontal, eine vertikale Halblinie, wobei deren tiefster Punkt
auf der höhe von py liegt.
• p Endpunkt von Linien-Segment q ⇒ ∗p (Bpq ) besteht, wenn q:
– nicht horizontal, aus zwei Halbgeraden mit Endpunkt p. Die eine
geht nach links-oben und die andere nach rechts-oben.
– horizontal, aus einer vertikalen Halblinie mit Endpunkt p, weil
die vertikale Halblinie unter p komplett auf den Punkt p transformiert wird.
• p Punkt und q ein nicht-inzidentes Linien-Segment ⇒ ∗p (Bpq ) ist, wenn
q:
8
– nicht horizontal, eine Parabel.
– horizontal und qy > py , das horizontale Liniensegment q.
• p, q Linien-Segmente ⇒ ∗p (Bpq ) ist, wenn:
– Bpq ein Segment ist, auch ein Segment.
– p und q horizontal mit gleichem Endpunkt, die vertikale Halblinie
mit Endpunkt im Schnitt von p und q, weil die vertikale Halblinie
unterhalb des Punktes komplett auf diesen transformiert wird.
Die Kanten von V ∗ können somit Teile von Linien, Parabeln und Hyperbeln sein. Für die Einteilung der transformierten Bisektoren in C − und C + ,
gehen wir immer von dem niedrigsten Punkt der Site aus und definieren den
Rest wie in Abschnitt 2.
Wir haben schon bei der Hilfstransformation ∗p gesehen, dass sie bei
vertikalen Geraden untehalb der Site daran scheitert 1 : 1 zu sein, weil diese
in einen einzigen Punkt p transformiert werden. Bei der Transformation ∗
gilt dieser kritische Fall auch und zusätzlich noch die weiteren Fälle:
• Punkt-Site z ist der untere Endpunkt einer Linien-Segment-Site.
• Kein Linien-Segment hat z als oberen Endpunkt.
• Es existiert eine Site p, deren y-Koordinate strikt unter zy ist, dann
schneidet die vertikale Halblinie unter p einige Punkte von V an der
Grenze von Rz . Dieser Punkt und z selbst, werden beide auf den gleichen Punkt nämlich z transformiert. Beachte, dass z in V sein muss,
solange z auf dem Bisektor liegt, der durch die Punkt-Site z und der
z-berührenden Linien-Segment-Site definiert wird.
3.4
Der Algorithmus für V ∗ und V
Wie wir bereists gesehen haben, gibt es bestimmte Situationen, in denen
V in V ∗ nicht 1 : 1 sind und sich somit topologisch unterscheiden. Es ist
einfacher mit einer veränderten Variante von Algorithmus 1, V und seine
Unterschiede zu V ∗ zu errechnen, als sofort V ∗ zu bestimmen.
Im Gegensatz zu Algorithmus 1 bearbeiten wir nun alle Ereignisse, die
mit einem Punkt in der Ebene verknüpft sind, auf einmal.
Die möglichen Ereignisse sind Schnitte von Grenzen, neue Sites, oder
beides. Wenn das Ereignis eine neue Site ist, dann gibt es zwei Fälle, die sich
darin unterscheiden, ob die Site im inneren einer anderen Voronoi-Region
liegt, oder auf einer Grenze.
Wir bearbeiten eine Linien-Segment-Site, wenn wir auf ihren lexikographisch letzten Endpunkt stossen. Folglich teilen wir die Segmente, die zu
einer Punkt-Site gehören, in diese, für die die Punkt-Site unterhalb des Endpunktes liegt und jene, bei denen die Punkt-Site dem Endpunkt liegt.
9
Nun könen wir für die einzelen Fälle analysieren, welche Aktionen bei
den verschiedenen Ereignissen ausgeführt werden:
• Wenn das Ereignis an einem Punkt p einfach nur der Schnitt von
Grenzen, oder eine isolierte Punkt-Site ist, dann ist die nötige Aktion
analog zu Algorithmus 1.
• Wenn p eine Punkt-Site und oberer Endpunkt eines Linien-Segmentes
ist, dann liegt p in Inneren der Voronoi-Region des Segmentes und der
Bisektor muss zwischen Punkt und Segment erstellt werden.
• Wenn p nun eine Punkt-Site und der untere Endpunkt eines Segments
ist und im Inneren einer Voronoi-Region um eine Site q liegt, dann
müssen zwei Bisektoren erstellt werden.
1. zwischen p und q.
2. zwischen p und der Segment-Site, mit der p verbunden ist.
Beachte, dass ∗ zwei Punkte von V auf p abbildet.
• Wenn p der untere Endpunkt mehrerer Segmente ist, und in der Region
um Site q liegt, dann ist die Situation ähnlich. Die nötigen Bisektoren
sind zwischen den Sites p und q, zwischen p und dem nächsten Segment, das gegen dem Uhrzeigersinn liegt und zwischen der Site p und
dem nächsten Segment, das im Uhrzeigersinn liegt.
• In den übrigen Fällen liegt die Punkt-Site p auf einer Grenze.
– Wenn p der obere Endpunkt von mindestens zwei Segmenten ist,
dann liegt p auf der Grenze die jedes benachbarte Paar von Segmenten trennt. Beachte, dass diese Grenzen erstellt wurden, bevor
wir p erreichen.
– Wenn p auf der Grenze zwischen zwei Sites q und r liegt und mindestens eines von beiden kein Segment ist, das mit p verbunden
ist, dann sind die nötigen Bisektoren ähnlich zu den vorherigen
Fällen. Hier ist es möglich, dass Knoten in V ohne Verbindungskante auf den selben Punkt in V ∗ abgebildet werden: der Mittelpunkt c eines Kreises, der auf seinem Rand die Punkte p, q, r hat
ist immer ein Knoten in V und es kann auch p ein Knoten von V
sein.
Theorem 3.4.1. Sei S eine Menge von Punkt- und Linien-Segment-Sites.
Dann können V , oder V ∗ mit einer Laufzeit von O(n log(n)) und einem
Speicherplatzbedarf von O(n) berechnet werden.
Beweis. Analog zu Abschnitt 2.
10
4
Gewichtete Punkt-Sites
Jede Site ist nun wieder eine Punkt-Site, die aber mit einem nichtnegativen Gewicht verknüpft ist. Die Logik hinter dem Voronoi-Diagramm ist die
Gleiche, nur benutzt man hier eine andere Metrik. Sie wird definiert, als die
Summe des Gewichtes und der euklidischen Distanz.
Die Unterschiede zum den VD aus Abschnitt 2 sind relativ klein. Die
Bisektoren sind hier teilweise Bereiche von Hyperbeln und die Regionen
einer Site können leer sein, wenn das Gewicht der Site grösser ist, als die
gewichtete Distanz von einigen anderen Sites.
Der Algorithmus hat zwei generelle Unterschiede:
1. Die Abbildung ∗ fixiert die Sites nicht mehr, sondern bildet sie nach
oben in der Länge ihres Gewichtes ab. Die Definition dazu lautet:
∀z ∈ R2 : ∗(z) = (x , y+ min(dp (z) + wp ) mit wp Gewicht der Site p.
2. Die Region einer Site p kann leer sein, wenn ∗(p)y < py + wp und kann
getestet werden, sobald p durch die Sweepline gefunden wird.
Insgesamt kann der Sweepline-Algorithmus, also wegen seiner guten
Lufzeit und seiner numerischen Stabilität sehr gut für angewandte Probleme benutzt und implementiert werden.
5
Schlussfolgerung
Der Algorithmus aus diesem Paper ist sehr effizient, doch bevor er implementiert wird müssen das Stabilitätsverhalten und einige Spezialfälle gesondert
betrachtet werden.
Der Sweepline-Algorithmus muss Bisektoren erstellen und Schnitte von
Linien bestimmen, genau wie jeder andere VD-Algorithmus. Zusätzlich wird
im Sweepline-Algorithmus noch die Transformation verarbeitet, welche die
numerische Stabilität gewährleistet. Denn solange die Transformation mathematisch gesehen 1 : 1 ist, kann sie entfernte Punkte sehr nah zusammen
abbilden.
Die meisten instabilen Fälle von ∗ können durch das Ausführen von
geometrischen Operationen auf untransformierte Objekte beseitigt werden.
11