11. Weitere Aspekte 11.1. Aktien mit Dividendenzahlungen 11.2

11. WEITERE ASPEKTE
11.
101
Weitere Aspekte
11.1. Aktien mit Dividendenzahlungen
Betrachten wir das Black–Scholes-Modell. Falls die Aktie nun Dividenden bezahlt,
wird der Wert der Aktie um den Wert der Dividenden grösser sein. Sei {Dt } der
Dividendenprozess. Dann ist der Barwert der Dividenden im Interval (t, T ] zum
Zeitpunkt t
i
hZ T
∗
−r(s−t)
IIE
e
dDs Ft .
t
Somit muss der Aktienkurs folgendermassen gegeben sein
i
hZ T
∗
St = IIE
e−r(s−t) dDs + e−r(T −t) ST Ft ,
t
da man ST als Dividendenzahlung im Zeitpunkt T auffassen kann. Der Wert der
Aktie lässt sich als Wert der zukünftigen Dividendenzahlungen im Intervall (t, ∞)
auffassen.
Berechnet man nun den Wert einer Option, dann muss man den Wert der Dividenden im Interval (t, T ] berücksichtigen; das heisst, modellieren. Diese Dividenden
bekommt man ja nicht ausbezahlt, wenn man die Option hält. Man beachte, dass
Rt
{e−rt St } kein Martingal mehr ist, sondern {St e−rt + 0 e−rs dDs }.
11.2. Devisenoptionen
Eine typische Anwendung von Optionen sind Optionen auf Devisen. Zum Beispiel,
eine grosse deutsche Chemiefirma will eine Firma in den USA übernehmen. Sie
unterbreitet den Aktionären ein Angebot, so dass die Firma in einem halben Jahr
eine Million Dollars benötigt. Nun will sich die deutsche Firma absichern, und kauft
daher eine Option über eine Million Dollars zum Ausübungspreis von 1 Million Euro.
Nun liegt das Riskio bei der Bank, die die Option ausstellt.
Der Wechselkurs {Xt } kann man dann zum Beispiel mit einer geometrischen
Brownschen Bewegung modellieren
Xt = X0 exp{σWt + (µ − σ 2 /2)t} .
Nehmen wir (im deutschen Markt) einen risikolosen Zins mit Intensität r an, erhalten
wir den Optionspreis
e−r(T −t) IIE∗ [(M Xt − K)+ | Ft ] ,
102
11. WEITERE ASPEKTE
L
KP
K
KC
A
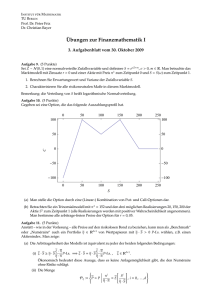
Abbildung 11.1: Auszahlungsfunktion des Straddle, Strangle, Spread und Butterfly.
wobei M die Anzahl Devisen im Vertrag bezeichnet. Wir sehen, dass auch hier
die Black–Scholes-Formel gilt. Man bemerke, dass die Absenz von Arbitrage den
Zinssatz im Ausland festlegt. Wir werden dies hier aber nicht beweisen.
11.3. Kombination von Optionspositionen
11.3.1.
Straddles
Ein Straddle ist das gleichzeitige Kaufen einer Call- und Put-Option mit dem
gleichen Ausübungspreis, also mit Auszahlung
(ST − K)+ + (K − ST )+ = max{ST − K, K − ST } = |ST − K| .
11.3.2.
Strangles
Ein Strangle ist auch ein gleichzeitiges Kaufen einer Call- und Put-Option, wobei die Ausübungspreise sich unterscheiden. Dabei ist der Call-Ausübungspreis KC
grösser als der Put-Ausübungpreis KP . Die Auszahlung ist dann
(ST − KC )+ + (KP − ST )+ = max{ST − KC , KP − ST , 0} .
Es ist zu bemerken, dass im Fall KC < KP der Betrag KP − KC immer ausbezahlt
wird. Man könnte diesen Vertrag somit als Kombination der Auszahlung KP − KC
11. WEITERE ASPEKTE
103
mit einem Strangle mit vertauschten Ausübungspreisen betrachten, da
(ST − KC )+ + (KP − ST )+ = (ST − KP )+ + (KC − ST )+ + KP − KC .
11.3.3.
Spreads
Ein Call-Spread ist der Kauf einer Call-Option und gleichzeitige Verkauf einer CallOption mit höherem Ausübungspreis
(ST − K)+ − (ST − A)+ = min{(ST − K)+ , A − K} ,
wobei A > K. So ein Kontrakt schützt den Käufer vor dem Risiko, das er eingeht,
wenn der Markt sich “nomal” verhält. Die Auszahlung kann wegen der Put-CallParität auch mit Put-Optionen und einem Barwert erhalten werden
(K − ST )+ − (A − ST )+ + (A − K) .
Ein Put-Spread ist Kauf und Verkauf von Putoptionen
(A − ST )+ − (K − ST )+ = min{(A − ST )+ , A − K} .
11.3.4.
Butterflies
Ein Butterfly wird durch den Kauf von zwei Call-Optionen mit verschiedenen Ausübungspreisen A und L und dem Verkauf von zwei Call-Optionen mit einem Ausübungspreis K dazwischen erzeugt,
(ST − L)+ + (ST − A)+ − 2(ST − K)+ .
Oft wählt man dabei K = (L + A)/2.
11.4. Spezielle Optionen
Call- und Put-Optionen sowie deren Kombinationen sind etablierte Optionen. Sie
werden an der “normalen” Börse gehandelt. Man nennt dies Optionen auch plain
Vanilla. Daneben gibt es auch nicht-so-übliche Optionen. Diese werden ausserhalb
der “normalen” Börse gehandelt, und man nennt sie over-the-counter, oder kurz
OTC. Wir wollen hier ein paar dieser Optionen vorstellen.
104
11.4.1.
11. WEITERE ASPEKTE
Asiatische Optionen
Eine Voraussetzung der üblichen Modelle ist, dass der Markt genügend liquide ist, so
dass ein einzelner Händler die Preise nicht direkt beeinflussen kann. Aber in vielen
Bereichen ist der Markt nicht genügend liquide. Zum Beispiel, der Aktiv wird nicht
täglich gehandelt, oder der Preis wird durch politische Entscheide bestimmt, oder
ein paar wenige Händler kontrollieren die Preise des zugrundeliegenden Aktivs. Ein
Beispiel eines solchen Marktes ist der Rohölmarkt. Zeichnet man jetzt eine Option
auf so einen Aktiv, kann es sein, dass die eine Partei die Möglichkeit hat, den Preis
zum Zeitpunkt T stark zu beinflussen. Um diesen Einfluss zu verkleinern, nimmt man
daher einen Durchschnittspreis über eine bestimmte Periode statt des Endpreises in
die Option
k
+
1 X
St` − K
,
k `=1
wobei 0 < t1 < · · · < tk = T . Eine Version der Option ist der floating Strike,
k
1 X +
St
,
ST −
k `=1 `
wobei hier tk < T gilt. Die stetigen Versionen der Option sind
1 Z T
+
Ss ds − K
T −t t
und
Z t
+
1
ST −
Sv dv
,
t−s s
wobei 0 ≤ t < T und 0 ≤ s < t ≤ T . Dadurch wird sichergestellt, dass eine
Manipulation des Marktes über einen längeren Zeitraum sehr kostspielig ist.
11.4.2.
Optionen auf Futures
Statt eines Aktivs kann auch der Preis eines Futures (das heisst die Grösse Ft , die
den Dividendenfluss bestimmt) einer Option zugrundeliegen. Optionen auf Futures werden vor allem zur Wertsicherung verwendet. Da das Kaufen und Verkaufen
des Aktivs mit Unkosten verbunden ist, und daher in der Realität eine theoretisch
gute Hedgingstrategie sehr teuer ist, versucht man mit Optionen auf Futures die
Hedgingstrategie zu approximieren. Das Problem ist aber, dass das Anwenden einer
solchen Strategie nur funktionieren kann, wenn faire Futurespreise im Markt existieren. Im weiteren, muss das Hedging-Portfolio mit dem Portfolio, das dem Futures
unterliegt, stark korreliert sein.
11. WEITERE ASPEKTE
11.4.3.
105
Optionen auf Optionen
Eine weitere Möglichkeit sind Optionen auf Optionen (compound Options). Hier
wählt man als unterliegenden Aktiv eine Option. Sei U > T . Dann lässt sich zum Beispiel als unterliegenden Aktiv eine Call-Option mit Ausübungszeitpunkt U wählen.
Bei einer Call-Option hat dann der Halter das Recht, aber nicht die Verpflichtung
zum Zeitpunkt T die Option mit Ausübungszeitpunkt U für einen bestimmten Preis
A zu kaufen. Der Wert der Option zum Zeitpunkt 0 wird also
o
i
+ i
o h n Z U
h n Z T
∗
∗
+ r(s) ds (SU − K) FT − A
.
r(s) ds IIE exp −
IIE exp −
0
T
Der Vorteil dieser Option ist, dass ihr Preis weniger stark fluktuiert als der Preis
einer gewöhnlichen Option.
11.4.4.
Barrieren-Optionen
Oft benutzt man eine Option nur dazu, um sich vor eher unwahrscheinlichen Ereignissen zu schützen. Daher hat man die sogenannten Barriere-Optionen eingeführt.
Bei diesen Optionen tritt die Option erst in Kraft (oder verliert ihren Wert) falls
der unterliegende Aktiv eine bestimmte Grenze erreicht. Das heisst, nicht nur der
Endwert des Aktivs spielt eine Rolle, sondern der gesamte Pfad.
Sei {St } der Preis des Aktivs, Mt = sup{Ss : 0 ≤ s ≤ t} und mt = inf{Ss :
0 ≤ s ≤ t}. Die Auszahlung eines Up-and-In-Call ist dann (ST − K)+ 1IMT ≥B für
K < B und S0 < B. Man bemerke, dass B ≤ K keinen Sinn macht, da diese
Option einer normalen Call-Option entspricht. Das Gegenstück ist ein Down-andIn-Call, (ST − K)+ 1ImT ≤B S0 > B. Ist B ≤ K, so hat die Option beim Erreichen der
Barriere noch keinen Wert, sondern muss zuerst zum Wert K zurückkehren. Diese
beiden Optionen nennt man Knock-In-Optionen.
Bei einer Knock-Out-Option wird die Option wertlos, falls die Barriere erreicht
wird. Man hat den Up-and-Out-Call (ST − K)+ 1IMT <B für K < B und S0 > B,
und den Down-and-Out-Call (ST − K)+ 1ImT >B für K > B und S0 > B. Analoge
Optionen erhält man auch, wenn man den Call durch einen Put ersetzt. Ob B > K
oder K > B hängt davon ab, welche der Optionen Sinn machen.
Eine Version der Barrieren-Option sind die Knock-Out-Optionen mit Prämie.
In diesem Fall wird eine eine fixe Prämie fällig, falls die Barriere erreicht wird.
Die Barrieren müssen auch nicht konstant über die Zeit sein, sondern können in
verschiedenen Perioden verschieden gewählt werden. Da gibt es auch die Variante,
106
11. WEITERE ASPEKTE
wo die Barriere in einem bestimmten Zeitraum erreicht oder nicht erreicht werden
soll. Also z.B., die Option wird in einem Jahr ausgeübt, aber nur, wenn der Preis
in den Monaten 3-9 die Barriere nicht überschreitet. Weiter gibt es die sogenannten
Tunnel-Optionen. Bei dieser Version gibt es sowohl eine obere wie auch eine untere
Schranke, die nicht erreicht werden sollen. Bei der Pariser-Option muss die Barriere
für eine bestimmte Zeitspanne über-, bzw. unterschritten werden.
Die Berechnung der Optionenpreise sind im allgemeinen recht kompliziert. Für
das Black–Scholes Modell aber, kann man geschlossene Formeln für die Preise erhalten, da die gemeinsame Verteilung von (ST , MT ) und (ST , mT ) berechnet werden
kann, siehe Hilfssatz D.1.
11.4.5.
Digitale Optionen
Ähnlich wie Barrieren-Optionen funktionieren die sogenannten digitalen Optionen.
Bei digitalen Optionen wird ein bestimmter Wert ausbezahlt, falls MT ≥ B oder
mT ≤ B. Hier sind auch Kombinationen möglich, wie z.B. 1IMT ≥B 1ImT >b für ein
b < S0 < B. Hier wird die Option wertlos, falls ein bestimmter Wert unterschritten
wird, erhält aber erst einen Wert, falls eine bestimmte obere Schranke erreicht wird.
11.5. Portfolio Insurance
Ein professioneller Inverstor muss oft eine Mindestrendite erziehlen, z.B. in der
Lebens- oder Pensionsversicherung. Zu diesem Zwecke muss ein Anlageportfolio abgesichert werden. Eine einfache Möglichkeit ist, auf einem Teil des Portfolios PutOptionen zu kaufen. Der versicherte Teil hat dann den Wert M [ST + (K − ST )+ ] =
M max{ST , K}, wobei M die Anzahl Aktien bezeichnet, die versichert sind.
Das Problem mit dieser Strategie ist, dass Put-Optionen im Normalfall nicht so
lange Laufzeiten haben, wie sie der Investor benötigt. Die Black–Scholes-Theorie
erlaubt aber nun, virtuelle Optionen zu erzeugen. Der Wert einer Put-Option ist
nach der Black–Scholes-Formel
Ke−r(T −t) Φ(−d2 ) − St Φ(−d1 ) .
Der Investor muss also KΦ(−d2 ) in den risikolosen Aktiv investieren, und Φ(−d1 )
Aktien verkaufen, das heisst, er sollte Φ(d1 ) Aktien behalten. Verhält sich also der
Markt wirklich wie ein Black–Scholes-Modell, dann würde diese Strategie den Wert
11. WEITERE ASPEKTE
107
max{ST , K} ergeben. Auf diese Weise hat der Investor eine virtuelle Put-Option
erzeugt, die sein Portfolio versichert.
Ein Problem der Portfolio Insurance ist, dass die Strategie stetiges Handeln voraussetzt. Dies ist nicht möglich, da die Börse nicht 24 Stunden an sieben Tagen die
Woche geöffnet ist. Weiter kann wegen der Transaktionskosten nicht stetig gehandelt
werden. Ein weiteres Problem ist, dass das Black–Scholes-Modell nur bedingt den
Markt beschreibt. Es gibt immer wieder “Crashes”, wo die Preise grosse Sprünge
aufweisen. Diese Sprünge können durch politische Erreignisse oder Katastrofen erzeugt werden. Oder es kann auch zu Liuiditätsengpässen kommen, wenn z.B. viele
Computer verkaufen wollen. Dann wird der Preis wegen des grossen Angebots sinken,
und noch mehr Händler, die die Black–Scholes-Formel verwenden, werden verkaufen
wollen.
Um das Risiko von Verlusten bei Preis-Sprüngen zu verkleinern, kann man die
sogenannte Constant-Proportion-Portfolio-Insurance anwenden. Hier teilt man die
Anlageperiode in n kleinere Perioden auf, in denen man ein konstantes Portfolio
hält. Das heisst, man wählt die Handelszeitpunkte 0 = t0 < t1 < · · · < tn = T . Zum
Zeitpunkt 0 hat man das Anfangsvermögen V0 und einen Startfloor F0 = cV0 , wobei
c ∈ (0, 1). Dies ergibt das sogenannte Start-Cushion (Startkissen)
C0 = V0 − F0 = (1 − c)V0 .
Man hat dann einen Wert m ∈ IIN, genannt Multiplikator, der angibt, wie hoch
die Aktienquote ist, die man haben will. Die Start-Exposure wird dann
E0 = mC0 .
Man hat eine Konstante α gewählt, die angibt, welchen Anteil man höchstens in Aktien investieren darf. Diese Konstante kann auch vom Gesetz vorgeschrieben sein.
Für einen dänischen Lebensversicherer gilt zum Beispiel α ≤ 0.7. Für Investmentfonds kann dies auch das Risikoprofil des Anlegers angeben. Der absolute Umfang
der Investition wird dann
A0 = min{mC0 , αV0 } ,
oder der Anteil der in die Aktien investiert wird, beträgt
o
n mC
0
,α .
q0 = min
V0
Zum Umschichtungszeitpunkt tn wird wie folgt verfahren. Man hat den Floor Fn .
Der kann z.B. konstant sein, Fn = F0 , oder er kann nachgezogen sein, Fn = F0 ertn ,
108
11. WEITERE ASPEKTE
das heisst, er folgt einer Mindestverzinsung. Ist das Cushion Cn = Vn − Fn , so wählt
man
o o
n
n mC
n
,α ,0 .
qn = max min
Vn
Liegt man also unter dem Floor, darf nicht in Aktien investiert werden. Je höher
man also über dem Floor liegt, umso mehr wird man in Aktien investieren. Man
sieht nun auch die Rolle von m. Je höher m, umso mehr investiert man in Aktien.
Zum einen ist somit ein grosses m wünscheswert, da man so eine hohe erwartete
Rendite erziehlt. Zum andern will man m klein halten, weil man dadurch das Risiko
vergrössert.