Übung 2 für die Klasse 10c

Übungen für die Prüfung über Ostern
Aufgabe 1: (Lösung: 24,7 cm)
Im Trapez ABCD sind gegeben:
BC = BD = 6,0 cm
 = 49,0° und
1 = 69,0°
Berechne den Umfang des Trapezes ABCD.
Aufgabe 2: (Lösung: x = 2 und y = – 1 )
Löse das Gleichungssystem
x  2y
 2x  3
(1)
4
(2) 6x – 4(x – 2y) = x + 6y
Aufgabe 3: (Lösung: D=R\{-2; 0} und L={1})
Gib die Definitions- und Lösungsmenge der Gleichung rechts an.
Aufgabe 4: (Lösung: a) Patricia hat Recht, Schenkellänge jeweils 20 LE und Pyth
und b) P(0/7) und Q(-3/-2), T(-1,5/0,25) und Nachweis ergibt: Behauptung stimmt)
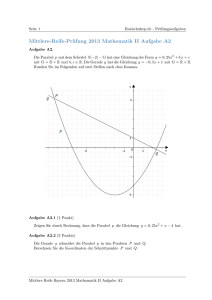
4a) Die Parabel p1 mit dem Scheitelpunkt S1 hat die Gleichung y = x2 – 4x +1.
Die nach oben geöffnete Normalparabel p2 mit dem Scheitelpunkt S2 geht durch die Punkte
A (– 5 / 8 ) und B ( 0 / 3 ).
Patricia zeichnet das zugehörige Schaubild und gewinnt den Eindruck, das Dreieck S1BS2 sei
gleichschenklig und rechtwinklig. Hat Patricia Recht? Begründe deine Entscheidung rechnerisch
oder durch Argumentation (Abmessen ist nicht zulässig).
4b) Eine nach oben geöffnete Normalparabel p1 hat den Scheitelpunkt S1 (–3 / –2 ).,
Die Parabel p2 hat die Gleichung y = – x2 + 7.
Berechne die Koordinaten der Schnittpunkte von p1 und p2.
Die Parabel p2 wird auf der y-Achse verschoben, bis sie mit der Parabel p1 genau einen
gemeinsamen Punkt T hat. Diese verschobene Parabel mit dem Scheitelpunkt S3 heißt p3.
Berechne die Koordinaten von T.
Überprüfe die Behauptung „Der Punkt T halbiert S1 S 3 “ durch Rechnung oder durch
Argumentation (Abmessen ist nicht zulässig).
Aufgabe 5:
(Lösung: ORest =) 2155 cm2)
Aus einem Zylinder wird eine Halbkugel herausgearbeitet.
Das Volumen dieser Halbkugel beträgt 262 cm3.
Es gilt:
h1 = 11,2 cm und
f = 6,8 cm
Berechne die Oberfläche des Restkörpers
Aufgabe 6: (Lösung: D=R\{-3; -1} und L={0; 1})
Gib die Definitions- und Lösungsmenge der Gleichung an:
Aufgabe 7:
(Lösung: eventuell Wertetabelle und mögliche Gerade z.B. y =0,5x+5})
1
Eine nach unten geöffnete Parabel p hat die Gleichung y =  x 2  4,5 .
2
Zeichne die Parabel in ein Koordinatensystem.
Gib eine Gerade g an, die durch den Punkt Q ( 4 / 7 ) geht und keinen gemeinsamen Punkt mit der
Parabel p hat.
Aufgabe 8:
(Lösungen zu a) Gerade 1: y = -1,5x+2,5 und Gerade 2: y=0,5x-3,5 und T(3/-2) ; mögliche
Parabelgleichungen haben die Form y = - x2+c, wobei c>2,5 sein muss)
Lösung zu b): A = 6 FE und P2(2/5) )
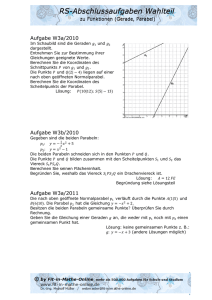
8a) Das Schaubild zeigt die Geraden g1 und g2. Bestimme die
Gleichungen der beiden Geraden.
Berechne die Koordinaten des Schnittpunktes T der beiden
Geraden.
Der Punkt T ist gleichzeitig Scheitelpunkte einer nach oben
geöffneten Normalparabel p1.
Eine nach unten geöffneten Normalparabel p2, deren Scheitelpunkt auf der y-Achse liegt, schneidet die Parabel p1 in zwei
Punkten.
Gib die Gleichung einer möglichen Parabel p2 an und überprüfe
durch Rechnung.
8b) Die Parabel p hat die Gleichung y = x2 + 2x – 3.
Die Schnittpunkte N1 und N2 mit der x-Achse und der
Schnittpunkt P1 mit der y-Achse bilden ein Dreieck N1P1N2.
Berechne den Flächeninhalt des Dreiecks N1P1N2.
Der Parabelpunkt P2 ist ein weiterer Punkt. Er liegt auf dem
rechten Parabelast. Das Dreieck N1N2 P2 hat einen
Flächeninhalt von 10 FE. Berechne die Koordinaten des Punktes P2.
Aufgabe 9: (Lösung: 51 m)
Im Rahmen einer Flugschau sollen zwei Flugzeuge mit je einer
Spannweite von 30 Metern unter einer parabelförmigen Brücke auf
gleicher Höhe nebeneinander durchfliegen.
Dabei soll jedes Flugzeug einen seitlichen Sicherheitsabstand von 50
m zur Brückenkonstruktion und 50 m zum Nebenmann haben.
Der Brückenbogen ist in seinem Scheitel 100 m hoch und am Fuß der
Brücke 300 m breit. Auf welcher Höhe über dem Boden fliegen die
Flugzeuge unter der Brücke hindurch?
Aufgabe 10: (Lösung: V Kegel=119cm3 ; Neigungswinkel 61,8°)
Die Mantellinien AS und BS des Kegels legen das Dreieck ABS fest.
AB = 6,0 cm
Es gilt:
AABS = 25,5 cm2 (Flächeninhalt des Dreiecks ABS)
Der Neigungswinkel zwischen der Dreiecksfläche ABS und der
Grundfläche des Kegels beträgt 75,0°. Berechne das Volumen des Kegels.
Die Spitze S des Kegels bewegt sich auf der Körperhöhe, bis der
neue Kegel das halbe Volumen hat. Seine Spitze heißt S1.
Berechne den Neigungswinkel zwischen der Dreiecksfläche ABS1 und der Grundfläche des Kegels.
Aufgabe 11: (Lösung: Unterschied 65,5 cm2)
Die Ecken eines Quadrats werden in gleicher Weise
abgeschnitten (Skizze). Es entsteht ein regelmäßiges Achteck.
Es gilt: x = 3,0 cm
Das ursprüngliche Quadrat und das regelmäßige Achteck sind
jeweils Grundflächen einer Pyramide mit der Höhe h = 12,5 cm.
Um wie viel cm2 unterscheiden sich die Oberflächen
der beiden Körper?
Aufgabe 12: (Lösung:
gemeinsamer Punkt (3/ -8), Stella hat nicht Recht.
Verschobene Gerade y = -2x+2 oder y= -2x+14)
a) Das Schaubild zeigt Ausschnitte einer Normalparabel p
und einer Geraden g.
Stella vermutet: “Aus der Zeichnung kann man ablesen, dass
die Gerade und die Parabel keinen gemeinsamen Punkt
haben.“
Hat Stella Recht? Begründe deine Aussage rechnerisch.
Die Gerade g wird anschließend parallel verschoben, sodass
sie durch einen der gemeinsamen Punkte der Parabel und der
x-Achse verläuft. Gib eine mögliche Gleichung der
verschobenen Geraden h an.
b) (Lösung: Dreieck ist nicht gleichschenklig, die Schenkel sind 20 LE und 18 LE lang.)
1
Die Parabel p1 hat die Gleichung y = – x 2  3 . Sie schneidet die x-Achse in den Punkten N1
3
(mit x > 0) und N2.
Eine nach oben geöffnete Normalparabel p2 geht durch den Scheitelpunkt von p1 und durch N1. Die
beiden Scheitelpunkte der Parabeln bilden mit N1 ein Dreieck. Ist dieses Dreieck gleichschenklig?
Begründe deine Antwort.
Aufgabe 13: (Lösung: Flächeninhalt 1 = 10FE; und S2 (4 / – 4))
Eine Parabel p1 hat die Gleichung y = x2 – 6x + 5. Die Schnittpunkte der Parabel mit den Achsen
bilden ein Dreieck. Berechne den Flächeninhalt des Dreiecks.
Die Parabel p1 wird parallel zur x-Achse nach rechts verschoben. Dadurch entsteht eine Parabel p2. Die
Schnittpunkte der Parabel p2 mit den Achsen bilden ebenfalls ein Dreieck. Dieses neu entstandene
Dreieck hat einen Flächeninhalt von 24 FE.
Welche Koordinaten hat der Scheitelpunkt S2 der Parabel p2?