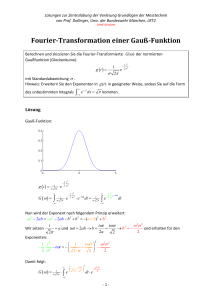
Rechnernutzung in der Physik

Rechnernutzung in der Physik
Teil3:StatistischeMethodenderDatenanalyse
Karlsruher Institut für Technologie, Wintersemester 2012/2013
U. Husemann
3
Statistische Methoden der Datenanalyse
3.1
Einführung in das Datenanalyse-Framework ROOT (0.5 VL)
Erste Schritte mit ROOT; Makros und kompilierte Programme;
Datenmodell; Graphen; Histogramme; Funktionen; Anpassungsrechung.
3.2
3.3
Grundlagen der Statistik (1.5 VL)
3.2.1.
Vorhersagbare und zufällige Prozesse; Messen und Statistik;
3.2.2.
Wahrscheinlichkeit als relative Häufigkeit; Kolmogorov-Axiome;
Venn-Diagramme; bedingte Wahrscheinlichkeit; Satz von Bayes;
Satz von der totalen Wahrscheinlichkeit; Denkschulen in der
Statistik.
3.2.3.
Zufallsvariable; PDF und CDF; Quantile; Median.
3.2.4.
Multivariate PDFs; Randverteilung; bedingte Verteilung.
3.2.5.
Erwartungswert; algebraische Momente; Varianz und Kovarianz;
Korrelationen.
3.2.6.
Funktionen von Zufallsvariablen; Gauß’sche Fehlerfortpflanzung
Beispiele für Wahrscheinlichkeitsverteilungen (1 VL)
3.3.1.
Binomialverteilung und Multinomialverteilung
3.3.2.
Poisson-Verteilung
3.3.3.
Gauß’sche Normalverteilung; Gauß’sche
Wahrscheinlichkeitsintervalle, Multivariate Gauß-Verteilung;
Gauß-Verteilung als Grenzfall; Zentraler Grenzwertsatz.
3.3.4.
Gleichverteilung; Exponentialverteilung; logarithmische
Normalverteilung; χ2-Verteilung; Cauchy-Lorentz-Verteilung.
Inhaltsangabe Rechnernutzung Teil 3, Wintersemester 2012/2013
1/2
3.4
3.5
3.6
Monte-Carlo-Methoden (0.5 VL)
3.4.1.
Zufallszahlen; linear-kongruente Zufallszahlengeneratoren;
Mersenne-Twister.
3.4.2.
Methoden zur Erzeugung von Zufallszahlen:
Transformationsmethode, Verwerfungsmethode,
Majorantenmethode;
3.4.3.
Anwendungen der Monte-Carlo-Methode.
Parameterschätzung (2 VL)
3.5.1.
Stichproben; Prüfgrößen; Schätzfunkionen: Konsistenz,
Erwartungstreue, Effizienz, Genauigkeit.
3.5.2.
Likelihood-Funktion; Maximum-Likelihood-(ML-)Prinzip; Varianz
von ML-Schätzern: grafische Methode und Bootstrapping.
3.5.3.
Methode der kleinsten Quadrate (LS); χ2-Funktion und χ2Wahrscheinlichkeit; LS-Schätzer für lineare Probleme; χ2Anpassung in der Praxis; Vergleich mit ML-Methode; Anpassung
an Histogramme.
3.5.4.
Fehlerbalken und Vertrauensintervalle; Neyman-Konstruktion
Hypothesentests (0.5 VL)
3.6.1.
Übersicht statistische Testverfahren.
3.6.2.
Signifikanzniveau und p-Wert; Fehler erster und zweiter Art;
Teststärke.
3.6.3.
Likelihood-Qutient; Pearson’scher χ2-Test; Kolmogorov-SmirnovTest.
Inhaltsangabe Rechnernutzung Teil 3, Wintersemester 2012/2013
2/2