5 1.FouriertrafoGauss

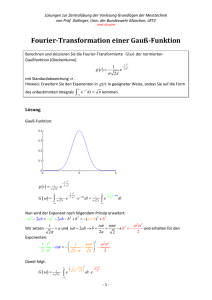
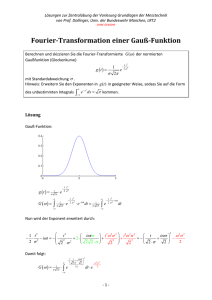
Lösungen zur Zentralübung der Vorlesung Grundlagen der Messtechnik
von Prof. Dollinger, Univ. der Bundeswehr München, LRT2
‐ OHNE GEWÄHR ‐
Fourier‐Transformation einer Gauß‐Funktion
Berechnen und skizzieren Sie die Fourier‐Transformierte G( ) der normierten
Gaußfunktion (Glockenkurve)
1 t2

1
2
g t  
e 2
 2
mit Standardabweichung  .
Hinweis: Erweitern Sie den Exponenten in g (t ) in geeigneter Weise, sodass Sie auf die Form
des unbestimmten Integrals


e  x dx   kommen.
2

Lösung
Gauß‐Funktion:
g t  
1
 2
G   
e
1 t2
  2
2



1
2
e
1 t2
  2
2
e
 it

dt  
1
2
e
1 t2
  2  i t
2
dt

Nun wird der Exponent nach folgendem Prinzip erweitert:
 a 2  2ab   a 2  2ab  b 2  b 2  (a  b) 2  b 2
Wir setzen
t
it i
 2 2
2
 a und it  2ab  b 

b  
und erhalten für den
2a
2
2
2
Exponenten:
1 t2
i   2 2
 t
  2  it   

  2
2 
2 
 2 
2
Damit folgt:
G   

1
 2
e
i 
 t



2 
 2 
2
dt  e

 2 2
2

‐1‐
Nun substituieren wir:
t
i

ˆ z
2 
2
und damit
dz
1

 dt  2   dz
dt
2 
Damit ergibt sich:
 

2
1
G   
 e 2   e  z dz  2  
 2

2
 G   
1
 G    e
1
  2 2
2

e

2
 2 2
2

 
Graphische Darstellung:
Die Standardabweichung ist proportional zur "Breite" der Glockenkurve (Normalverteilung).
die "Öffnung" der Kurve bei halber Höhe des Maximums entspricht etwa
2  2 ln 2    2,35 (FWHM = Full Width at Half Maximum).
Im Zeitraum ergibt sich die breite blaue Kurve mit der Standardabweichung t  
1
Im Frequenzraum ergibt sich die schmale grüne Kurve mit der Standardabweichung  

G(ω)
2

2
g(t)
t

/>
Die Fourier‐Trafo einer Gauß‐Kurve mit der Standardabweichung 
ergibt also wieder eine Gauß‐Kurve mit der Breite 1/.
‐2‐
Zusatzbemerkung:
Die Gauß‐Funktion hat in der Physik/Quantenmechanik eine große Bedeutung, da sie
Wahrscheinlichkeitsverteilungen bzw. die Unschärfe Δx bei Messungen beschreibt. Der
Zusammenhang der Fourier‐Transformation gilt für alle korrespondierenden Messgrößen,
z.B. Ort/Impuls, Frequenz/Zeit oder äquivalent Energie/Zeit und deren Messungen in einem
Experiment und führt zur Heisenbergschen Unschärferelation für jeweils diese
korrespondierenden Größen:

 p x 
 p   x  h
2
ebenso findet man
E  t  h f  t  1
‐3‐