2.4. Funktionen in der Betriebswirtschaft Bemerkungen

2.4. Funktionen in der Betriebswirtschaft
Bemerkungen:
• Wirtschaftliche Zusammenhänge werden häufig durch stetige
Funktionen (i.A. auf D(f ) ⊂ [0, ∞)) beschrieben, auch wenn
Stückzahlen o.ä. modelliert werden
• Modellierung komplexer (und von zufälligen Schwankungen beeinflusster) realer Zusammenhänge durch möglichst einfachen Funktionstypen (→ Statistik, Interpolation, Approximation) häufig aus
empirischen Daten gewonnen
• ökonomische Funktionen, die konkav und monoton wachsend sind,
heißen neoklassisch.
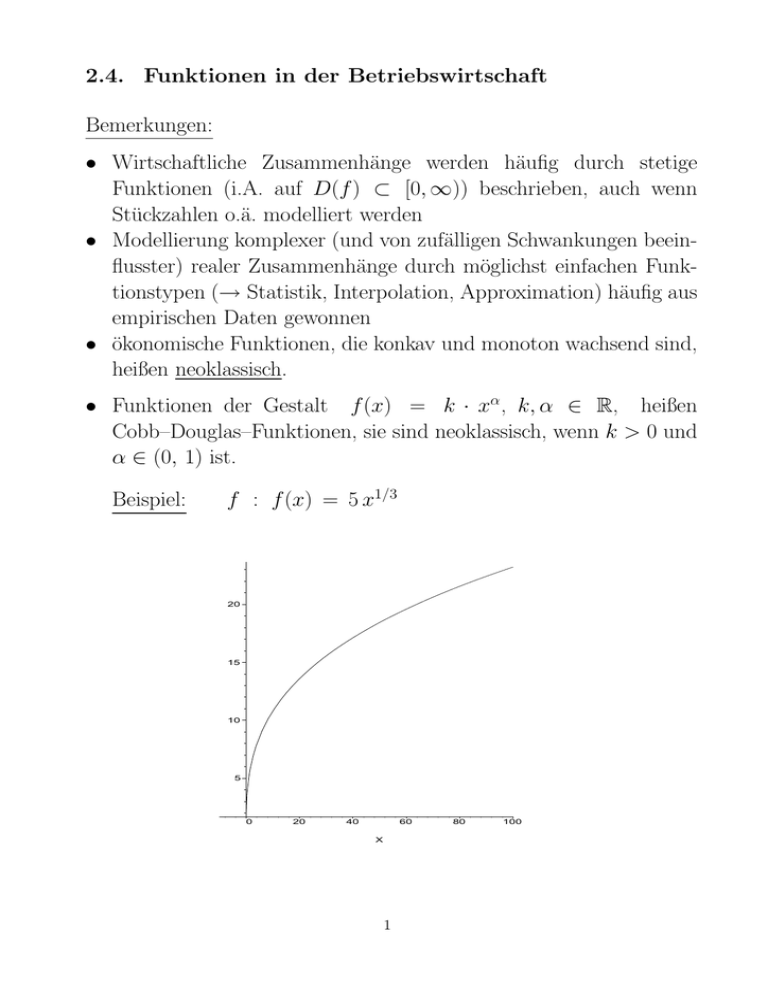
• Funktionen der Gestalt f (x) = k · xα , k, α ∈ R, heißen
Cobb–Douglas–Funktionen, sie sind neoklassisch, wenn k > 0 und
α ∈ (0, 1) ist.
Beispiel:
f : f (x) = 5 x1/3
20
15
10
5
0
20
40
60
X
1
80
100
Beispiele
(1) Angebotsfunktion x = x(p) ,
Bedeutung:
p≥0
Angebotsmenge in Abhängigkeit vom erzielbaren Preis
positiv, monoton wachsend, i.a. mit Sättigungswert
Eigenschaften:
Beispiel:
x(p) = 10 · (1 − e
2−p
3
), p ∈ [2, ∞)
10
8
6
4
2
0
5
10
15
20
P
2
25
30
(2) Preis–Absatz–
Funktion
x = x(p), D(x) = {p, p ≥ 0 und x(p) ≥ 0}
p = p(x), D(p) = {x, x ≥ 0 und p(x) ≥ 0}
Bedeutung:
Absatzmenge in Abhängigkeit vom Preis
bzw. erzielbarer Preis in Abhängigkeit von
der abzusetzenden Menge
beide Funktionen sind zueinander invers
(Umkehrfunktion), beide monoton fallend
x(p) = 250−2.5 p ⇐⇒ p(x) = 100−0.4 x
D(x) = [0, 100], D(p) = [0, 250]
Eigenschaften:
Beispiel:
(3) Erlös- bzw.
E(x) = x · p(x) ,
Umsatzfunktion E(p) = p · x(p) ,
Bedeutung:
D(E) = D(p)
D(E) = D(x)
Erlös/Umsatz in Abhängigkeit vom Absatz
oder vom Preis
im monopolistischen Fall degressiv wachsend
bis Erlösmaximum, dann fallend
E(x) = 100x − 0.4 x2 , x ∈ D(E) = [0, 250]
E(p) = 250p − 2.5 p2 , p ∈ D(E) = [0, 100]
Eigenschaften:
Beispiel:
6000
6000
5000
5000
4000
4000
3000
3000
2000
2000
1000
1000
0
50
100
150
200
250
0
20
40
60
P
X
3
80
100
(4) Kostenfunktion
K(x) = Kf + Kv (x) , x ∈ D(K) = [0, ∞),
Kf ≥ 0 : Fixkosten,
Kv (x) : variable Kosten
Bedeutung:
Produktionskosten in Abhängigkeit von der
Produktionsmenge
positiv, monoton wachsend
Eine Kostenfunktion heißt ertragsgesetzlich,
wenn sie auf [0, xS ] degressiv wachsend und
auf [xS , ∞) progressiv wachsend ist;
xS heißt dann Schwelle des Ertragsgesetzes.
K(x) = 0.01x3 − x2 + 60x + 800 , x ≥ 0 ,
xS = 100
3 ,
Kf = 800 , Kv (x) = 0.01x3 − x2 + 60x
Eigenschaften:
Beispiel:
6000
5000
4000
3000
2000
1000
0
20
40
60
X
4
80
100
K(x)
x
(5) Stückkostenfunktion
Bedeutung:
k(x) =
(6) variable
Stückkosten
Bedeutung:
kv (x) =
,
x ∈ (0, ∞)
Produktionskosten je Mengeneinheit in
Abhängigkeit von der Produktionsmenge
Eigenschaften: positiv, monoton fallend auf (0, x0], monoton
wachsend auf [x0, ∞);
Das Minimum k(x0) der Stückkosten heißt
Betriebsoptimum;
k(x0) stellt (langfristig) die untere Schranke für
den Preis dar, nur oberhalb dieser Schranke
kann noch ohne Verlust produziert werden.
Beispiel:
k(x) = 0.01x2 − x + 60 + 800
x , x > 0,
x0 = 60.8152 , k(x0) = 49.3243 ist langfristiges Preisminimum.
Kv (x)
x
,
x ∈ (0, ∞)
variabler Teil der Produktionskosten, bezogen
auf eine Mengeneinheit des Outputs, in
Abhängigkeit von der Produktionsmenge;
Eigenschaften: positiv, monoton fallend auf (0, xm], monoton
wachsend auf [xm, ∞), Das Minimum kv (xm)
der variablen Stückkosten heißt Betriebsminimum, kv (xm) stellt (kurzfristig) die untere
Schranke für den Preis dar, nur oberhalb dieser Schranke können noch die laufenden Kosten
der Produktion gedeckt werden.
Beispiel:
kv (x) = 0.01x2 − x + 60 , x > 0 ,
xm = 50 , kv (xm) = 35 ist kurzfristiges Preisminimum, bei dem nur noch die laufenden
Kosten gedeckt werden!
5
300
250
200
150
100
50
0
50
100
150
200
X
10000
8000
6000
4000
2000
0
50
100
150
X
–2000
–4000
6
200
250
(7) Gewinnfunktion G(x) = E(x) − K(x) ,
D(G) = D(p)
Deckungsbeitrag D(x) = E(x) − Kv (x) = G(x) + Kf ,
D(D) = D(p)
Bedeutung:
Gewinn (Deckungsbeitrag) in Abhängigkeit
vom Output
Eigenschaften: monoton wachsend bis zum Gewinnmaximum
xGmax = xDmax , danach progressiv fallend
Beispiel:
G(x) = −0.01x3 + 0.6x2 + 40x − 800 ,
x ∈ [0, 250] ,
xGmax = 61.63332 , Gmax = 1603.28843
G(x)
= p(x) − k(x) ,
x
D(g) = D(p) \ {0}
Bedeutung:
Gewinn je Mengeneinheit in Abhängigkeit vom
Output
Eigenschaften: monoton wachsend bis zum Stückgewinnmaximum xgmax , danach progressiv fallend
Beispiel:
g(x) = −0.01x2 +0.6x+40− 800
x , x ∈ (0, 250] ,
xgmax = 47.6311 , gmax = 29.0957
(8) Stückgewinnfunktion
g(x) =
30
1500
20
1000
500
10
0
20
40
60
80
100
0
X
20
40
60
X
–500
–10
7
80
100
(9) Produktionsfunktion
x(r) ,
D(x) ⊂ [0, ∞)
Bedeutung:
Output in Abhängigkeit vom Input r
Eigenschaften: monoton wachsend;
meist bis zu einer Sättigungsgrenze xmax
Beispiel:
x(r) = ³
1
1
2
+r
− 12
´2 ,
r ∈ (0, ∞) ,
xmax = lim x(r) = 4
r→∞
4
3
2
1
0
10000
20000
r
8
30000
40000