2.Kap.
Werbung
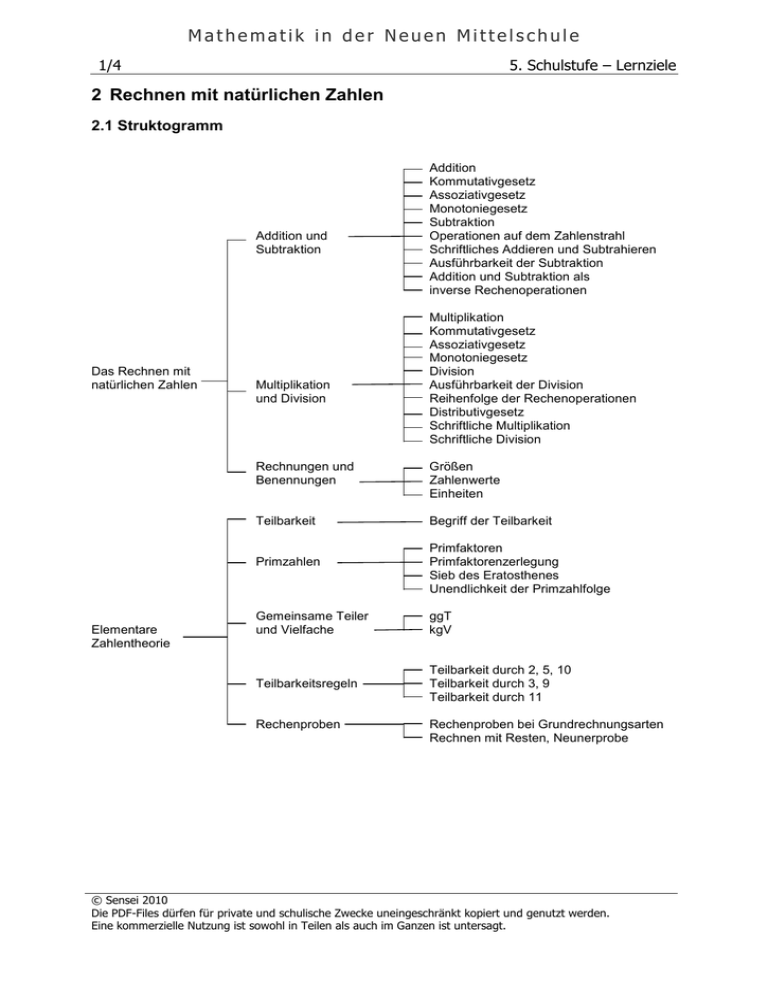
Mathematik in der Neuen Mittelschule 1/4 5. Schulstufe – Lernziele 2 Rechnen mit natürlichen Zahlen 2.1 Struktogramm Addition und Subtraktion Das Rechnen mit natürlichen Zahlen Multiplikation und Division Multiplikation Kommutativgesetz Assoziativgesetz Monotoniegesetz Division Ausführbarkeit der Division Reihenfolge der Rechenoperationen Distributivgesetz Schriftliche Multiplikation Schriftliche Division Rechnungen und Benennungen Größen Zahlenwerte Einheiten Teilbarkeit Begriff der Teilbarkeit Primzahlen Elementare Zahlentheorie Addition Kommutativgesetz Assoziativgesetz Monotoniegesetz Subtraktion Operationen auf dem Zahlenstrahl Schriftliches Addieren und Subtrahieren Ausführbarkeit der Subtraktion Addition und Subtraktion als inverse Rechenoperationen Primfaktoren Primfaktorenzerlegung Sieb des Eratosthenes Unendlichkeit der Primzahlfolge Gemeinsame Teiler und Vielfache ggT kgV Teilbarkeitsregeln Teilbarkeit durch 2, 5, 10 Teilbarkeit durch 3, 9 Teilbarkeit durch 11 Rechenproben Rechenproben bei Grundrechnungsarten Rechnen mit Resten, Neunerprobe © Sensei 2010 Die PDF-Files dürfen für private und schulische Zwecke uneingeschränkt kopiert und genutzt werden. Eine kommerzielle Nutzung ist sowohl in Teilen als auch im Ganzen ist untersagt. Mathematik in der Neuen Mittelschule 2/4 5. Schulstufe – Lernziele 2.2 Lernziele natürliche Zahlen Addition a Bei der Addition wird aus Summanden eine Summe gebildet a Die Reihenfolge der Summanden bei der Addition von ist beliebig (Kommutativgesetz) a Die Reihenfolge der Zusammenfassung von Summanden bei der Addition ist beliebig (Assoziativgesetz) d Mit Hilfe von Klammern kann die Reihenfolge festgelegt werden. e Die Kleiner-Beziehung zwischen zwei natürliche Zahlen bleibt erhalten, wenn zu beiden die gleiche Zahl addiert wird (Monotoniegesetz) Subtraktion a Die Subtraktion ist die Umkehroperation zur Addition b Man gelangt von der Addition, wenn man bei bekannter Summe nach einem Summanden fragt c Das Ergebnis der Subtraktion heißt Differenz d Bei der Subtraktion von natürlichen Zahlen darf der Minuend nicht keiner sein als der Subtrahend Operationen erster Stufe am Zahlenstrahl a Addition und Subtraktion natürlicher Zahlen lassen sich als Streckenaddition und Streckensubtraktion am Zahlenstrahl darstellen Schriftliches Addieren a Summanden werden stellenwertrichtig untereinander geschrieben b Die Addition beginnt bei den Einern c Überschreitet bei einer Spaltenaddition die nächste Stellenzahl, wird der entsprechende Betrag übertragen. d Addition ohne Überschreiten der dezimalen Einheit e Addition mit Überschreiten der dezimalen Einheit Schriftliches Subtrahieren a b c d e f g Multiplikation a b c d Division a b c d Ausführbarkeit der Division a Die Division natürlicher Zahlen ist nicht immer ohne Rest ausführbar b Die Division durch null ist unmöglich Subtraktionen können als Wegnehmen oder als Ergänzen gedeutet werden Wegnehmen: 7 weniger 3 ergibt 4 Ergänzen: von 3 bis 7 ist 4 Der Subtrahend wird stellenwertrichtig unter den Minuend geschrieben Die Subtraktion beginnt bei den Einern Subtraktion ohne Überschreiten der dezimalen Einheit Subtraktion mit Überschreiten der dezimalen Einheit Die Multiplikation ist die Addition mehrerer gleicher Summanden Multiplikator mal Multiplikand ist gleich dem Produkt Multiplikand und Multiplikator werden Faktoren genannt Die Faktoren eines Produkts dürfen vertauscht werden (Kommutativgesetz) e Sind drei Zahlen miteinander zu multiplizieren, ist die Reihenfolge der Zusammenfassung ohne Einfluss auf das Ergebnis (Assoziativgesetz) f Werden die Faktoren einer Multiplikation mit der gleichen Zahl multipliziert, bleibt die Kleiner-Bezihung erhalten (Monotoniegesetz) Divisionen können als Teilen oder als Enthaltensein gedeutet werden Teilen: 12 Äpfel werden in 4 gleiche Teile geteilt Enthaltensein: wie oft sind 4 cm in 12 cm enthalten Die Division ist die Umkehroperation zur Multiplikation © Sensei 2010 Die PDF-Files dürfen für private und schulische Zwecke uneingeschränkt kopiert und genutzt werden. Eine kommerzielle Nutzung ist sowohl in Teilen als auch im Ganzen ist untersagt. Mathematik in der Neuen Mittelschule 3/4 5. Schulstufe – Lernziele Reihenfolge der Rechenoperationen a Die Rechenoperation höherer Stufe wird immer zuerst ausgeführt b Durch Klammern kann die Reihenfolge der Rechenoperationen festgelegt werden c Rechenoperationen in Klammern werden zuerst ausgeführt Distributivgesetz a Das Distributivgesetz drückt einen Zusammenhang zwischen Rechenoperationen verschiedener Stufe aus b Distributivgesetz a · (b + c) = a • b + a • c mit a ≠ 0 Schriftliche Multiplikation a Im Prinzip: 2 356 • 473 = = 2 356 • (400 + 70 + 3) = = 2 356 • 4(00) + 2 356 • 7(0) + 2 356 • 3 = = 9 424(00) + 16 492(0) + 7 068 = 1 114 388 b Statt Nullen anzuschreiben wird jedes Teilprodukt jeweils eine Stelle nach rechts ausgerückt. c Multiplikation mit einstelligem Multiplikator d Multiplikation mit mehrstelligem Multiplikator Schriftliche Division a Für alle natürlichen Zahl a, b, c (c ≠ 0) gilt: (a + b) : c = a : c + b : c b Dividenden werden in Einer, Zehner und Hunderter zerlegt; z.B. 86 : 2 = (80 + 6) : 2 = 80 : 2 + 6 : 2 = 40 + 3 = 43 c Das Produkt aus Quotient und Divisor ergibt den Dividenden; dies gilt auch für die Teilprodukte d Division mit einstelligem Divisor e Division mit mehrstelligem Divisor Größen Zahlenwert a Größen sind quantitativ bestimmbare Einheiten b Größen bestehen aus einem Zahlenwert und einer Einheit Einheiten a b c d Teilbarkeit ^ a Eine natürliche Zahl ist durch eine andere Zahl teilbar, wenn sie darin ohne Rest enthalten ist b Die Zahl 0 ist durch alle natürlichen Zahlen ≠ 0 teilbar c Jede natürliche Zahl ≠ 0 ist durch sich selbst und durch 1 teilbar Primzahlen a Zahlen, die nur durch 1 und sich selbst teilbar sind, heißen Primzahlen b 1 zählt nicht zu den Primzahlen; die Primzahlen beginnen bei 2 Primfaktorenzerlegung a Jede natürliche Zahl ist entweder eine selbst eine Primzahl oder lässt sich in ein Produkt von Primzahlen zerlegen b Primfaktoren können auch durch den Euklidischen Algorithmus zerlegt werden Sieb der Eratothenes a Man schreib eine Folge natürlicher Zahlen an und streicht alle Zahlen, die durch 2, 3, … teilbar sind b Die nicht gestrichenen Zahlen sind Primzahlen Einheiten sind physikalische Größen Längenmaße Zeitmaße Massenmaße Unendlichkeit der a Es gibt unendlich viele Primzahlen Primzahlfolge b Euklid bewies dies indirekt, dass es keine größte Primzahl geben kann. Größter gemeinsamer Teiler a Haben zwei Zahlen gemeinsame Teiler, so haben sie auch einen ggT b Haben zwei Zahlen keinen gemeinsamen Teiler (außer 1), nennt man sie teilerfremd. © Sensei 2010 Die PDF-Files dürfen für private und schulische Zwecke uneingeschränkt kopiert und genutzt werden. Eine kommerzielle Nutzung ist sowohl in Teilen als auch im Ganzen ist untersagt. Mathematik in der Neuen Mittelschule 4/4 5. Schulstufe – Lernziele Kleinstes gemeinsames Vielfaches a Haben zwei Zahlen gemeinsame Vielfache, haben sie auch ein kgV b Es gibt unendlich viele gemeinsame Vielfache Teilbarkeit durch 2, 5, 10 a Durch 2 teilbar, wenn die letzte Ziffer durch 2 teilbar ist b Durch 5 teilbar, wenn die letzte Ziffer durch 5 teilbar ist (0 oder 5 ist) c Durch 10 teilbar, wenn die letzte Ziffer 0 ist Teilbarkeit durch 3, 9 a Durch 3 teilbar, wenn die Quersumme durch 3 teilbar ist b Durch 9 teilbar, wenn die Quersumme durch 3 teilbar ist Teilbarkeit durch 11 a Durch 11 teilbar, wenn die alternierende Quersumme durch 11 teilbar ist b Alternierende Quersumme: 8 5 9 7 6 8 + 9+ 6 = 23 5 + 7 = 12 Alternierende Quersumme: 23 – 12 = 11 Rechenproben bei Grundrechnungs arten a Jede Zahl hat bei der Division durch 9 den gleichen Rest wie ihre Quersumme b Beispiele Addition: Aufgabe Quersumme Neunerrest 3 964 22 4 4 722 15 6 10 ≡ 1 8 686 37 ≡ 1 Subtraktion: Aufgabe 7 428 3 986 3 442 Multiplikation: Aufgabe 617 • 382 = 234 694 Quersumme 21 26 13 ≡ 4 Neunerrest 3 -8 -5 ≡ 4 Quersumme 14 13 28 ≡ 1 Neunerrest 5• 4– 20 ≡ 2 Produkt falsch! c Für die Division gilt: Dividend = Divisor • Quotient + Rest © Sensei 2010 Die PDF-Files dürfen für private und schulische Zwecke uneingeschränkt kopiert und genutzt werden. Eine kommerzielle Nutzung ist sowohl in Teilen als auch im Ganzen ist untersagt.