Doppelter Schnittpunkt - walser-h-m.ch

Hans Walser, [20080910a]
Doppelter Schnittpunkt
1 Der Schnittpunkt
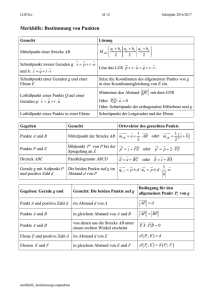
Wir beginnen mit einem Sehnensechseck A0 B2 A1B0 A2 B1 mit der Eigenschaft, dass die
an einer Ecke Bi anstoßenden Seiten jeweils gleich lang sind, also:
A1B0 = A2 B0 , A2 B1 = A0 B1, A0 B2 = A1B2
Dann haben die drei Geraden Ai Bi , i {0,1, 2} , einen gemeinsamen Schnittpunkt P
(Abb. 1).
B0
B0
A2
A2
B1
B1
P
A1
A1
A0
A0
B2
B2
Abb. 1 Sechseck und Schnittpunkt
Dieser Schnittpunkt P kann auf zwei Arten als „besonderer Punkt“ gesehen werden.
2 Inkreismittelpunkt
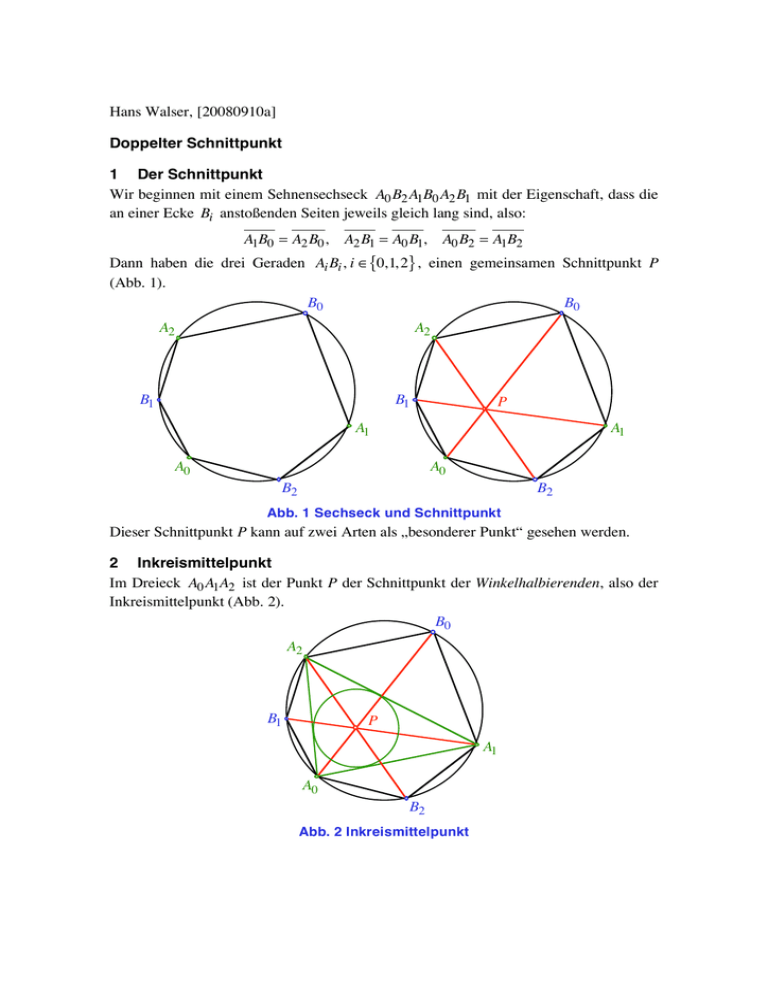
Im Dreieck A0 A1A2 ist der Punkt P der Schnittpunkt der Winkelhalbierenden, also der
Inkreismittelpunkt (Abb. 2).
B0
A2
B1
P
A1
A0
B2
Abb. 2 Inkreismittelpunkt
2/2
Hans Walser: Doppelter Schnittpunkt
Die Winkel A1A0 B0 und B0 A0 A2 sind nämlich Peripheriewinkel über gleich langen
Sehnen und daher gleich groß. Die Gerade A0 B0 halbiert also den Dreieckswinkel bei
A0 . Entsprechendes gilt für die beiden anderen Geraden.
Damit ist auch bewiesen, dass die drei Geraden Ai Bi , i {0,1, 2} , tatsächlich kopunktal
sind.
3 Höhenschnittpunkt
Die Abbildung 3 lässt vermuten, dass der Schnittpunkt P der Höhenschnittpunkt im
Dreieck B0 B1B2 ist.
B0
A2
B1
P
A1
A0
B2
Abb. 3 Höhenschnittpunkt
Dies ist tatsächlich der Fall.
Die Winkel A0 B1B2 und B2 B1A1 sind als Peripheriewinkel über gleich langen Sehnen gleich groß; dasselbe gilt für die Winkel B1B2 A0 und A2 B2 B1 . Die beiden
Dreiecke B1B2 A0 und B1B2 P sind daher spiegelbildlich bezüglich der Seite B1B2 .
Somit steht die Gerade A0 P , also die Gerade A0 B0 , senkrecht auf der Seite B1B2 und
ist eine Höhe des Dreieckes B0 B1B2 . Analog für die beiden anderen Geraden.