cl - home.hs-karlsruhe.de

C:\Si05\Ingmath\Sinus_an_aus\Bandsperre Pi-Freq-u-Sinus an-aus4.doc. 1/5
Homepage: http://www.home.hs-karlsruhe.de/~kero0001/
Bandsperre Pi, Frequenzbereich und Zeitbereich.
Ein-und Ausschalten Sinus am Filtereingang
Vergleiche folgenden Homepage-Text:
http://www.home.hs-karlsruhe.de/~kero0001/komplexefilter/Filterberechnung2.pdf
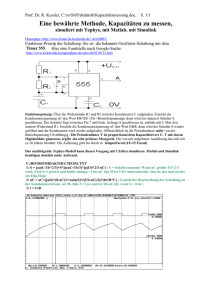
Daraus das linke Word-Bild:
u0
ik
Lp
R1
Cp
Lr
Cr
u1
Z1 Y1
Yp
Lp
R1
Cp
i1
R1
Lr
Cr
Zr
uA
u0
iCp
Lr
Cr
Z2
Y2
uC1
i2
uCp Lr
Cr
R1
uA
uC2
Bezeichnungen für Zeitbereich
Y1p
Typ 3: Bandsperre Pi-Glied
Z1=R1;
Y1=1/Zr;
Z2=1/Yp; Y2=1/R1+1/Zr;
Y1p=Y1+1/(Z2+1/Y2);
u1=u0/(1+Z1*Y1p); uA=u1/(1+Z2*Y2)
Beispiel-Aufrufe
clear;R1=50;Dw=0.2;wres=1;wS=0.9;dw=0.00101;wstart=0;wmax=2;bild=1;dt=0.01;As=1;tmax=500;t1=0;t2=tmax/2; Filtallg3
bild 1, Bandsperr-Pi,R1=50,Dw=0.2,BB=0.2081,Lr=227,Cr=0.0044,Lp=20.1,Cp=0.0497
0.7
0.6
0.6
angle(u2)/5000
0.4
imag(u2)
0.5
,wstart=0,wres=1
.
0.4
0.3
0.2
0
-0.2
0.2
-0.4
0.1
-0.6
0
0
0.5
1
w
1.5
abs(u2)
2
-0.2
0
0.2
real(u2)
0.4
C:\Si05\Ingmath\Sinus_an_aus\Bandsperre Pi-Freq-u-Sinus an-aus4.doc. 2/5
bild 2, Bandsperr-Pi,R1=50,Dw=0.2,BB=0.2081,wS=0.9
1
0.5
0
uA
-0.5
-1
-1.5
u0/2
0
50
100
150
200
250 t
300
350
400
450
500
Aufruf war:
clear;R1=50;Dw=0.2;wres=1;wS=0.9;dw=0.00101;wstart=0;wmax=2;bild=1;dt=0.01;As=1;tmax=500;t1=0;t2=tmax/2; Filtallg3
Erkenntis: Da die Sinuskreisfrequenz wS=0.9 ist, also kleiner als die Sperrkreisfrequenz wres= 1, kommt am Ausgang
des Sperrfilters (uA, siehe obige Schaltung, dort mit u2 bezeichnet) eine Spannung an, nämlich mit fast der halben Amplitude
wie der Sinus des Eingangs (u0).
Beachte, dass uA nach dem Start des Sinus einen gewissen „Einschwingvorgang und nach Nullwerden des Sinus einen
gewissen „Auschschwingvorgang“ hat. Das liegt an der „homogenen“ Lösung der DGL.
C:\Si05\Ingmath\Sinus_an_aus\Bandsperre Pi-Freq-u-Sinus an-aus4.doc. 3/5
bild 4, Bandsperr-Pi,R1=50,Dw=0.2,BB=0.2081,wS=1
0.5
0
uA
-0.5
u0/2
-1
-1.5
0
50
100
150
200
250
t
300
350
400
450
500
Aufruf war
clear;R1=50;Dw=0.2;wres=1;wS=1;dw=0.00101;wstart=0;wmax=2;bild=3;dt=0.01;As=1;tmax=500;t1=0;t2=tmax/2;Filtallg3
Erkenntnis: Da hier die Kreisfrequenz wS=1 des Sinus gleich der Sperrkreisfrequenz wres=1 ist, ist die
Ausgangsspannung uA, wie erwartet gleich null. Allerdings macht sich auch hier sowohl nach dem Start als auch nach
dem Ende des Sinus ein „Einschwingvorgang“ bemerkbar. Dass nach Ende des Sinus am Ausgang des Sperrfilters
„plötzlich“ eine Spannung entsteht, mag für den „Laien“ eine Überraschung sein. Natürlich liegt das wieder an der
„homogenen“ Lösung der DGL.
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
bild 6, Bandsperr-Pi,R1=50,Dw=0.2,BB=0.2081,wS=1.1
1
0.5
0
uA
-0.5
-1
u0/2
-1.5
0
50
100
150
200
250
t
300
350
400
450
500
Aufruf war
clear;R1=50;Dw=0.2;wres=1;wS=1.1;dw=0.00101;wstart=0;wmax=2;bild=5;dt=0.01;As=1;tmax=500;t1=0;t2=tmax/2;Filtallg3
Erkenntnis: Da hier wS=1.1 größer als die Sperrkreisfrequenz wres=1 ist, kommt am Ausgang uA etwa die halbe
Sinusamplitude an, ähnlich wie oben bei wS=0.9.(s. Bild 2). Auch hier natürlich wieder ein Einschwingvorgang und ein
Ausschwingvorgang infolge der homogenen Lösung der DGL.
Matlab-Datei Filtallg3.m
% Datei Filtallg3.m % Prof. Dr. R. Kessler
% Version 3: Mit Wahl der Sinusfrequenz ws
%clear;R1=50;Dw=0.2;wres=1;wS=0.9;dw=0.00101;wstart=0;wmax=2;bild=1;dt=0.01;As=1;tmax=500;t1=0;t2=tmax/2;Filtallg3
%clear;R1=50;Dw=0.2;wres=1;wS=1;dw=0.00101;wstart=0;wmax=2;bild=3;dt=0.01;As=1;tmax=500;t1=0;t2=tmax/2;Filtallg3
%clear;R1=50;Dw=0.2;wres=1;wS=0.1.1;dw=0.00101;wstart=0;wmax=2;bild=5;dt=0.01;As=1;tmax=500;t1=0;t2=tmax/2;Filtallg3
% vgl. Homepage: http://www.home.hs-karlsruhe.de/~kero0001/
% für alle vier Filtertypen Bandpass (Pi und T) Bandsperre (Pi und T)
%
% Die vier RLC-Schaltungen Bandpass/Bandsperre/ Pi /T
% werden in einer einzigen Datei berechnet
format compact;
FS=12; % Fontsize
Typ=3; % Bandsperre pi . Nnur dafür wir der Zeitbereich berechnet
C:\Si05\Ingmath\Sinus_an_aus\Bandsperre Pi-Freq-u-Sinus an-aus4.doc. 4/5
STyp= ['Bandpass- Pi'; % Aufruf als STyp(i,:), (i=1,2,3,4)
'Bandpass- T ';
'Bandsperr-Pi';
'Bandsperr-T '];
kwert= [1.786,0.459; 1.094,0.4795; 0.9099,2.2091 ; 0.5247, 2.2084];
k1=kwert(Typ,1); k2=kwert(Typ,2);
Lr= k1*R1/Dw;
Cr=1/(wres*wres*Lr);
Lp=k2*Lr*(Dw/wres)^2;
Cp=1/(wres*wres*Lp);
% Lr= Induktivität der Reihenschaltung
% Cr= Kapazität der Reihenschaltung
% Lp= Induktivität der Parallelschaltung
% Cp= Kapazität der Parallelschaltung
w=wstart:dw:wmax; % w= Vektor der Kreisfrequenz
ws=dw;
% ws = Schrittweite dw
s=j*(w+ws);
Zr=s.*Lr+1./(s.*Cr); % Impedanz der Reihenschaltung
Yp=s.*Cp+1./(s.*Lp); % Leitwert der Parallelschaltung
switch Typ
% vgl. die Schaltungen
case{1},Z1=R1; Y1=Yp; Z2=Zr ; Y2=1./R1+ Yp;
% Bandpass Pi
case{2},Z1= R1+ Zr; Y1= Yp; Z2= Zr; Y2= 1./R1;
% Bandpass T
case{3},Z1=R1; Y1=1./Zr; Z2=1./Yp; Y2=1./R1+1./Zr;
% Bandsperre Pi
case{4},Z1= R1+ 1./Yp; Y1= 1./Zr; Z2= 1./Yp; Y2= 1./R1; % Bandsperre T
end;
ST=[', ', STyp(Typ,:)];
Y1p=Y1+1./(Z2+1./Y2);
u1=1./(1+Z1.*Y1p);
u2=u1./(1+Z2.*Y2);
beu2=abs(u2);
Wiu2=angle(u2)*180/pi;
figure(bild); clf reset;
%Berechnung Bandbreite:
%Ziel: Bandbreite finden, dh. Abnahme von betrag(u2) auf Wert sw=0.5/sqrt(2)
% Methode Nullstellen finden für Funktion abs(u2)-sw
% Die Bandbreitenpunkte als Kreis malen
Beu2=abs(u2); sw =0.5/sqrt(2);
KN=0;
for k=2:length(Beu2),
if sign(Beu2(k-1)-sw) * sign(Beu2(k)-sw) <0, %Vorzeichenwechsel
KN=KN+1; Nrk(KN)=k; wN(KN)=w(k);
end;
end;
BB= wN(2)-wN(1); % BB= Bandbreite
subplot(1,2,1); % u.A. die Bandbreitenpunkte als Kreis malen
plot(w,abs(u2),'k', w, 0.6+0.0002*angle(u2)*180/pi,'k' ,...
wN(1),Beu2(Nrk(1)),'ko', wN(2),Beu2(Nrk(2)),'ko' );
grid on;
text(max(w),0,' abs(u2)');
text(min(w)+0.75*(max(w)-min(w)),0.58,'angle(u2)/5000');
k1=Lr * BB/R1;
k2= Lp/Lr * (wres/BB)^2; k12=[k1,k2];
S1=['.
bild ', num2str(bild)];
S2=[',R1=', num2str(R1)];
S3=[',Dw=', num2str(Dw)]; S4=[',wstart=',num2str(wstart)];
S5=[',wres=', num2str(wres)]; S6=[',wmax=',num2str(wmax)];
S6=[',BB=',num2str(BB,4)];
S10=[',Lr=',num2str(Lr,3)]; S11=[',Cr=',num2str(Cr,3)];
C:\Si05\Ingmath\Sinus_an_aus\Bandsperre Pi-Freq-u-Sinus an-aus4.doc. 5/5
S12=[',Lp=',num2str(Lp,3)]; S13=[',Cp=',num2str(Cp,3)];
S14=[',k1=',num2str(k1,4)]; S15=[',k2=',num2str(k2,4)];
tit1=[S1,ST,S2,S3,S6,S10,S11,S12,S13];
title(tit1,'Fontsize',FS);
xlabel('w','Fontsize',FS);
yL=[S4,S5]; ylabel(yL);
subplot(1,2,2);
plot(real(u2), imag(u2),'k',...
real(u2(Nrk(1)) ),imag(u2(Nrk(1) )),'ko',...
real(u2(Nrk(2)) ),imag(u2(Nrk(2) )),'ko');
xlabel('real(u2)','Fontsize',FS');
ylabel('imag(u2)','Fontsize',FS);
grid on; axis equal;
%+++++++++++++++++++++++++++++++++++++++++
% Jetzt Zeitbereich Typ 3, Bandsperre Pi:
%++++++++++++++++++++++++++++++++++++++++
pause;
Np=floor(tmax/dt);tp=zeros(Np,1); u0p=tp; uAp=tp;
% Startwerte:
t=0;i1=0; i2=0;ik=0; uC1=0;uC2=0; uCp=0;
k=0;
while t< tmax;
u0=As*sin(wS *t)*(t>t1)*(t<t2); % sinus der Kreisfrequenz wS von t1 bis t2
iCp= 1/(2*R1)*(u0- R1*(i1+ ik)-uCp -R1*(ik-i2) ); % Kondensatorstrom durch Cp
uC1= uC1+ i1*dt/Cr;
i1= i1+( u0 -R1*(i1+ iCp+ ik)- uC1 )*dt/Lr;
ik = ik +(uCp)*dt/Lp;
uCp= uCp + (iCp)*dt/Cp;
i2= i2 + ( R1*(ik +iCp - i2) - uC2)*dt/Lr;
uC2= uC2+ i2*dt/Cr;
k=k+1;
tp(k)=t; u0p(k)=u0;
uAp(k)= R1*(ik+ iCp- i2);
t= t +dt;
end;
bild= bild+1; figure(bild); clf;
ofs= As;
plot(tp,u0p/2-As, tp,uAp); grid on;
xlabel('t'); text(tmax,0,' uA'); text(tmax,-As,' u0/2');
S1=['bild ', num2str(bild)];
S7=[',wS=',num2str(wS,4)];
tit3=[S1,ST,S2,S3,S6,S7]; title(tit3,'Fontsize',FS);
%+++++++++++++++ Ende Datei Filtalg3.m +++++++++++++++++++