Tauchspulsystem: DGLn, Ersatzschaltung,

Prof. Dr. R. Kessler, FH-Karlsruhe, Sensorsystemtechnik, C:\ro\Si05\dgln\tauchsp\Tauchspul3.doc, S. 1/1
Homepage:
http://www.home.hs-karlsruhe.de/~kero0001
http://www.home.hs-karlsruhe.de/~kero0001/tauchspule/tauchspule.html
Tauchspulsystem: DGLn, Ersatzschaltung,
Simulationen im Zeitbereich u. Frequenzbereich
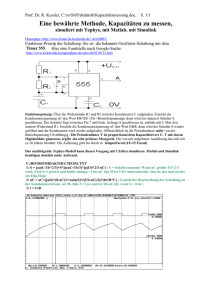
Physikalische Grundlagen des Tauchspul-Modells
Elektrik:
Spannung u0 , Strom i, Spuleninduktivität L, Spulenwiderstand R, induzierte Spannung kg*v.
v= Geschwindigkeit der Spule im Magnetfeld, kg = „Generatorkonstante“
i
R
L
u0
kg*v
Maschensatz : u0 = R*i + L*di/dt + kg*v (DGL für Strom i )
oder mit Operator s= d/dt
u0 = (R + L*s)*i + kg * v
Mechanik: Die elektrische Kraft Fel = km * i wirkt auf die Masse m, die mit Feder D und Reibelement r an
das Gehäuse des Tauchspulsystems gekoppelt ist. km = „Motorkonstante“. x = Position der Masse m.
Fel
D
m
r
x
Newton: m*dv/dt = Summe der auf m wirkenden Kräfte, folglich
m * dv/dt = km*i - D* x – r*v (DGL für Geschwindigkeit v )
v = dx/dt
(DGL für Position x )
Behauptung: Motorkonstante km = Generatorkonstante kg
Beweis mit Energieerhaltungssatz:
mechanische Leistung Pmech = Kraft Fel (= km* i ) mal Geschwindigkeit v, also Pmech = km* i * v
elektrische Leistung Pel = Strom i mal Spannung (= kg * v), also Pel = i * kg * v
Gleichsetzen Pmech = Pel, also km * i* v = i * kg * v ==> km = kg
Aufstellen einer elektrischen Ersatzschaltung des elektromechanischen Systems.
Ziel: die mechanischen Größen durch elektrische ersetzen. Mit dem Operator s = d/dt wird mit dv/dt = s*v und
mit x = v/s aus der DGL für v die Operatorgleichung m*s*v = km*i – D*v/s – r*v. Geordnet und v
ausgeklammert: (m*s + r +D/s )*v = km*i . Daraus v= km*i /( m*s + r + D/s). Diesen Ausdruck für v
eingesetzt in die obige Gleichung für u0 ergibt die Operatorgleichung für i
u0 = (R+ L*s) * i + i* kg*km/(m*s + r + D/s) oder i ausgeklammert und durch kg*km dividiert
u0 = (R + L * s +
1
) *i
m
r
D
*s +
+
kg * km
kg * km kg * km * s
Diese Formel legt nahe, den 3. Term aufzufassen als Parallel-Schaltung, darin
m
„mechanische Kapazität“
Cm =
kg * km
kg * km
„mechanischer Widerstand“ Rm =
r
kg * km
„mechanische Induktivität “ Lm =
D
Prof. Dr. R. Kessler, FH-Karlsruhe, Sensorsystemtechnik, C:\ro\Si05\dgln\tauchsp\Tauchspul3.doc, S. 2/2
Damit hat sich die Ersatzschaltung ergeben
u0 = (R + L * s +
i
R
1
) *i
1
1
Cm * s +
+
Lm * s Rm
L
u0
Cm
kg*v
Lm
Rm
Mit diesem Ersatzschaltbild könnte man z.B. PSPICE zum Simulieren verwenden.
An der Parallelschaltung liegt die Spannung kg*v. Daraus kann man mit PSPICE die Geschwindigkeit v
berechnen und durch Integration von v die Position x = ∫ v * dt .
Simulink-Schaltung zum Simulieren des Zeitbereichs:
Man hat ein System von drei linearen DGLn 1. Ordnung, hier noch mal hingeschrieben, aber der jeweilige
Differentialquotient auf der linken Seite:
di/dt = 1/L * ( u0 – R*i – kg*v)
dv/dt = 1/m * (km*i –D*x – r*v)
dx/dt = v
Daraus folgt sofort die zugehörige Simulink-Schaltung (Datei Tauchspul1.MDL).
Zum Verständnis dieser Schaltung braucht man lediglich zu wissen, dass der Block gain (das Dreieck)
die Eingangsgröße mit dem konstanten Faktor (der im Dreieck steht), multipliziert. Der Addierer ist
selbsterklärend, der Integrator 1/s liefert das Zeitintegral der Eingangsgröße. Die Blöcke To Workspace
liefern die berechneten Größen an die Kommandoebene von Matlab, so dass sie dort mit plot-Befehlen
gezeichnet werden können. Sowohl der Aufruf als auch die zeichnerische Darstellung werden im vorliegenden
Fall mit der Matlab-Datei tauchspulm3.m ausgeführt, die ihrerseits von der Matlab-Datei runtauchsp1.m
aufgerufen wird: in Kommandoebene eintippen runtauchsp1, dann die Eingabetaste.
Datei Tauchspul1.MDL
R.Kessler Juni 2004
DGLn:
di/dt = 1/L * ( u0 – R*i – kg*v)
dv/dt = 1/m * (km*i –D*x – r*v)
dx/dt = v
Aufruf z.B.mit
runtauchsp1
aP*(u > t1)*(t2 > u) + aS*sin(2*pi * fS * u)
Clock
Funktions-Generator: Puls und Sinus
u0
t
To Workspace
di/dt
kg
1
1/L
i
s
Gain
R
km
dv/dt
1/m
Integrator
1
v=dx/dt
s
r
D
1
s
v
x
Prof. Dr. R. Kessler, FH-Karlsruhe, Sensorsystemtechnik, C:\ro\Si05\dgln\tauchsp\Tauchspul3.doc, S. 3/3
Die Simulation im Frequenzbereich wird mit Matlab durchgeführt.
Benutzen wir das oben hergeleitete Ersatzschaltbild! Zunächst führen wir zur Abkürzung ein
Z = R+ L*s
die „Längsimpedanz“ der Ersatzschaltung
und den „Querleitwert“ der Ersatzschaltung Y = s*Cm + 1/(s*Lm) + 1/Rm
Dann ergibt sich
i = u0 / (Z+1/Y)
Der Strom i
und die Spannung kg*v am Querleitwert
kg*v = i /Y = u0 /(1+ Z*Y)
v = 1/kg * u0/(1+Z*Y)
und daraus die Geschwindigkeit v
x = v/s
und daraus die Auslenkung x
Für die komplexe Rechnung wird s = j*w (mit w = Kreisfrequenz, j = Wurzel aus minus eins)
% Datei runtauchsp1.m
R. Kessler Juni 2004
% Run-Datei für einige Tauchspulbeispiele
clear;bild=1;t1=0.01;t2=0.21;tmax=0.4;wmax=0.5e3;
kg=5;R=7.45;L=6e-3;D=1100;m=0.05;r=1e-6;aP=0.99;aS=0;wS=100;tauchspulm3;
disp('weiter mit beliebiger Taste'); pause;
clear;bild=3;t1=0.01;t2=0.21;tmax=0.2;wmax=0.5e3;
kg=5;R=7.45;L=6e-3;D=1100;m=0.05;r=1e-6;aP=0;aS=1;wS=100;tauchspulm3;
disp('weiter mit beliebiger Taste');pause;
clear;bild=5;t1=0.01;t2=0.21;tmax=0.2;wmax=0.5e3;
kg=5;R=7.45;L=6e-3;D=1100;m=0.05;r=1e-6;aP=0.0;aS=1;wS=148;tauchspulm3;
disp('weiter mit beliebiger Taste');pause;
clear;bild=7;t1=0.01;t2=0.21;tmax=0.4;wmax=0.5e3;
kg=5;R=2;L=6e-3;D=1100;m=0.05;r=1e-6;aP=0.99;aS=0;wS=148;tauchspulm3;
disp('weiter mit beliebiger Taste');pause;
clear;bild=9;t1=0.01;t2=0.21;tmax=0.4;wmax=0.5e3;
kg=5;R=20;L=6e-3;D=1100;m=0.05;r=1e-6;aP=0.99;aS=0;wS=148;tauchspulm3;
disp('weiter mit beliebiger Taste');pause;
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
Datei Tauchspulm3.m R. Kessler Juni 2004
Tauchspulsystem. Aufruf z.B. mit runtauchsp1
Für das Ersatzschaltbild: Zunächst führen wir zur Abkürzung ein
"Längsimpedanz" der Ersatzschaltung Z = R+ L*s
"Querleitwert" der Ersatzschaltung
Y = s*Cm + 1/(s*Lm) + 1/Rm
Es ergeben sich:
Strom
i = u0 / (Z+1/Y)
Spannung kg*v am Querleitwert kg*v = i /Y = u0 /(1+ Z*Y)
daraus die Geschwindigkeit
v = 1/kg * u0/(1+Z*Y)
daraus die Auslenkung
x = v/s
Für die komplexe Rechnung wird
s = j*w (mit w=Kreisfrequenz, j=Wurzel
aus minus eins)
Wichtig: bei Matlab muss man die "gliedweise" Multiplikation und Division
beachten, s.u.
Ausführung:
Beispielaufrufe: runtauchsp1
format compact; % verhindert unnötige Leerzeilen
% Berechnung der Ersatzgrößen:
km=kg;
fS=wS/(2*pi); % fS = Frequenz, wS = Kreisfrequenz des eingeprägten Sinus
Cm = m/(kg*km); % m= Masse
Rm = kg*km/r;
% r = Reibkonstante
Lm = kg*km/D;
% D = Federkonstante
% Strings erzeugen für Parameterausgabe:
Skg=['
kg=',num2str(kg)];
SR=[',R=',num2str(R)];
SL=[',L=',num2str(L)];
SD=[',D=',num2str(D)];
Sm=[',m=',num2str(m)];
SwS=[',wS=',num2str(wS)];
te=[Skg,SR,SL,SD,Sm,SwS]; % te = String mit Parameterwerten
Prof. Dr. R. Kessler, FH-Karlsruhe, Sensorsystemtechnik, C:\ro\Si05\dgln\tauchsp\Tauchspul3.doc, S. 4/4
% Zunächst komplexe Rechnung mit Matlab:
% beachte die "gliedweise" Multiplikation .* statt *
%
"gliedweise" Division
./ statt /
dw=wmax/1000; wst=dw;
w=wst:dw:wmax; % Vektor Kreisfrequenz, wst= Startwert >0
s= j*w;
% Vektor komplexer Operator s
Z = R+ L*s;
% Längsimpedanz der Ersatzschaltung
Y = s*Cm + 1./(s*Lm) + 1/Rm; % Querleitwert der Ersatzschaltung
u0k=1;
% Komplexe Amplitude der (gedachten) Sinuserregung
ik = u0k ./ (Z+1 ./Y);
% ik= Vektor der komplexen Stromstärke
vk = 1/kg * u0k ./(1+Z .* Y); % vk= Vektor der komplexen Geschwindigkeit
xk= vk ./s;
% xk= Vektor der komplexen Position
figure(bild); clf;
subplot(2,2,1);
% 2 Spalten, 2 Zeilen, Bildnummer 1 (oben links)
plot(w,abs(ik),w,abs(vk),w,100*abs(xk));grid on;
legend('ik','vk','100*xk');
xlabel('Kreisfrequenz w'); ylabel('Beträge');
title(te);
subplot(2,2,3);
% 2 Spalten, 2 Zeilen, Bildnummer 3 (unten links)
plot(w,angle(ik),w,angle(vk),w,angle(xk));grid on;
xlabel('Kreisfrequenz w'); ylabel('Winkel');
legend('ik','vk','xk');
subplot(2,2,2);
% 2 Spalten, 2 Zeilen, Bildnummer 2, oben rechts
hold on;
% warum Bild anhalten? Damit man die Kreise zeichnen kann, s.u.
plot(real(ik),imag(ik), real(vk),imag(vk), 100*real(xk),100*imag(xk));
ylabel('ortskurven');grid on;
% zusätzlich an Ortskurven Kreis beim 1. Punkt (drum vorher hold on) :
plot(real(ik(1)),imag(ik(1)),'o',...
real(vk(1)),imag(vk(1)),'o',...
100*real(xk(1)),100*imag(xk(1)),'o');
% Jetzt noch Kreuz x am Ende der Ortskurven:
imax=length(ik);
plot(real(ik(imax)),imag(ik(imax)),'x',...
real(vk(imax)),imag(vk(imax)),'x',...
100*real(xk(imax)),100*imag(xk(imax)),'x');
axis equal;
hold off;
% Damit die Kreise auch Kreise sind und nicht Ellipsen!
% jetzt hold off, damit nachfolgendes keinen Unsinn macht
% Jetzt mit Simulink den Zeitbereich simulieren:
if bild == 1 tauchspul1;end; % bei Bild=1 Simulinkschaltung auf Bildschirm
sim('tauchspul1');
% Simulieren mit Simulink-Datei tauchspul1.mdl
figure(bild+1); clf;
hold on;
% Warum hier hold on? Um die Achsen zu zeichnen (s.u.)
of1=0.005; of2=0.010;of3=0.015; % Offsets
plot(t,u0/100, t,v/10+of1,t,10*x+of2,'k', t,i/10+of3); grid on;
ta=[0,tmax];
% ta= x-Vektor zum Zeichnenen der Achsen
plot(ta,[0,0],ta,[of1,of1],ta,[of2,of2],'k',ta,[of3,of3]); % Achsen zeichnen
ofte=0.001;
% Offset für nachfolgende "Kurvenbeschriftung"
text(0.005+tmax,0+ofte,'u0/100'); % Kurvenbeschriftung
text(0.005+tmax,0+of1+ofte,'v/10');
text(0.005+tmax,0+of2+ofte,'x*10');
text(0.005+tmax,0+of3+ofte,'i/10');
xlabel('Zeit t');
title(te); % Im Titel stehen einige Parameter
hold off;
% Damit nachfolgende Plotbefehle keinen Quatsch machen
% Ende Matlab-Datei Tauchspulm3.m
Prof. Dr. R. Kessler, FH-Karlsruhe, Sensorsystemtechnik, C:\ro\Si05\dgln\tauchsp\Tauchspul3.doc, S. 5/5
kg=5,R=7.45,L=0.006,D=1100,m=0.05,wS=100
0.25
0.15
0.05
ik
ortskurven
Beträge
ik
vk
100*xk
vk
0.2
ik
0.1
0
-0.05
vk
0.05
-0.1
100*xk
0
0
100
100*xk
200
300
Kreisfrequenz w
400
500
-0.05
0
0.05
0.1
0.15
0.2
4
ik
vk
xk
2
Winkel
ik
0
vk
-2
xk
-4
0
100
200
300
Kreisfrequenz w
400
500
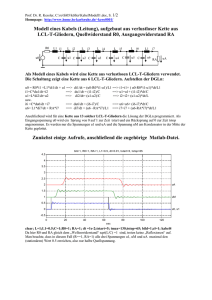
Figur oberhalb: Erkenntnisse aus den Frequenzgängen:
Strom ik wirkt wie „Bandsperre“,
Geschwindigkeit vk wirkt wie „Bandpass“, Auslenkung xk wirkt wie „Tiefpass“ (mit Resonanzüberhöhung)
Die Resonanzkreisfrequenz liegt bei etwa w=148 /sec
kg=5,R=7.45,L=0.006,D=1100,m=0.05,wS=100
0.035
0.03
i/10
0.025
0.02
x*10
i/10
0.015
u0/100
x*10
0.01
v/10
v/10
0.005
u0/100
0
-0.005
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
Zeit t
Figur oberhalb: Sprungantworten Strom i, Geschwindigkeit v Auslenkung x.
Auffällig ist die anfängliche „Spitze“ im Stromverlauf (beim Ein-und Ausschalten) der Spannung u0: Sie
entsteht durch die bei der mechanischen Bewegung entstehenden Induktionsspannung kg*v (vgl DGLn)
Prof. Dr. R. Kessler, FH-Karlsruhe, Sensorsystemtechnik, C:\ro\Si05\dgln\tauchsp\Tauchspul3.doc, S. 6/6
kg=5,R=7.45,L=0.006,D=1100,m=0.05,wS=100
0.03
0.025
i/10
0.02
i/10
0.015
x*10
0.01
x*10
0.005
v/10
u0/100
0
v/10
-0.005
u/100
-0.01
0
0.02
0.04
0.06
0.08
0.1
0.12
0.14
0.16
0.18
0.2
Zeit t
Figur oberhalb: Sinusantworten bei Kreisfrequenz wS = 100/sec, also unterhalb der „Resonanzfrequenz“.
Man vergleiche die Phasenwinkel mit den Kurven der komplexen Frequenzgänge: Strom i und Auslenkung
x haben gleichen Phasenwinkel (etwas nacheilend gegenüber u0), v eilt 90 Grad vor (bezogen auf x)
kg=5,R=7.45,L=0.006,D=1100,m=0.05,wS=148
0.025
i/10
0.02
i/10
0.015
x*10
0.01
x*10
0.005
v/10
u0/100
0
v/10
-0.005
-0.01
u0/100
-0.015
0
0.02
0.04
0.06
0.08
0.1
0.12
0.14
0.16
0.18
0.2
Zeit t
Figur oberhalb: Sinusantworten bei „Resonanzkreisfrequenz“ wS = 148 /sec. Auffällig ist, dass der Strom i
nur einige gedämpfte Schwingungen macht und dann null wird. Das entspricht dem Frequenzgang (s.o.),
nämlich Strom hat Eigenschaft einer Bandsperre. Dagegen sind die mechanischen Größen Geschwindigkeit
v und Auslenkung groß: sie sind jetzt in Resonanz (vgl wieder die Frequenzgänge!) Auch die Phasenwinkel
entsprechen den Frequenzgängen: Geschwindigkeit v ist gleichphasig mit Erregerspannung u0, Auslenkung
x ist 90 grad nacheilend.
Prof. Dr. R. Kessler, FH-Karlsruhe, Sensorsystemtechnik, C:\ro\Si05\dgln\tauchsp\Tauchspul3.doc, S. 7/7
kg=5,R=2,L=0.006,D=1100,m=0.05,wS=148
0.5
0.2
ik
0.4
0.1
ik
vk
100*xk
vk
ortskurven
Beträge
ik
0.3
0.2
0
100*xk
-0.1
0.1
100*xk
vk
-0.2
0
0
100
200
300
Kreisfrequenz w
400
500
0
0.2
0.4
4
Winkel
2
ik
ik
vk
xk
0
vk
-2
xk
-4
0
100
200
300
400
Kreisfrequenz w
500
Figur oberhalb: Spulenwiderstand R sehr klein gewählt ( 2 Ohm statt 7.45 Ohm). Dadurch ist die „Güte“
sehr verringert: Bandsperre ( Kurve ik) und Bandpass (Kurve vk ) sind „sehr breit“. Tiefpass (Kurve xk) hat
keine Resonanzüberhöhung mehr
kg=5,R=2,L=0.006,D=1100,m=0.05,wS=148
0.07
0.06
i/10
0.05
0.04
x*10
0.03
0.02
i/10
x*10
0.01
v/10
u0/100
0
v/10
u0/100
v/10
-0.01
-0.02
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
Zeit t
Figur oberhalb: Sprungantworten bei Spulenwiderstand sehr klein ( 2 Ohm statt 7.45 Ohm) Dadurch kaum
noch Schwingung im Zeitbereich (Kurve Auslenkung x und Kurve Geschwindigkeit v). Aber Strom i zeigt
noch deutlicher die „Spitze“ beim Spannungssprung. Diese Stromkurve ähnelt jetzt dem Einschalt-und
Ausschalt-Strom beim elektromagnetischen Relais. (vgl. meine homepage: http://www.home.fhkarlsruhe.de/~kero0001/relais/relaisdynamik.html
Prof. Dr. R. Kessler, FH-Karlsruhe, Sensorsystemtechnik, C:\ro\Si05\dgln\tauchsp\Tauchspul3.doc, S. 8/8
kg=5,R=20,L=0.006,D=1100,m=0.05,wS=148
0.25
0.05
ik
ortskurven
Beträge
ik
vk
100*xk
vk
0.2
0.15
0.1
0
-0.05
vk
100*xk
0.05
0
-0.1
ik
0
100
200
300
Kreisfrequenz w
400
500
100*xk
-0.05
0
0.05
0.1
0.15
0.2
4
ik
vk
xk
Winkel
2
ik
0
vk
-2
xk
-4
0
100
200
300
400
Kreisfrequenz w
500
Figur oberhalb: Jetzt Spulenwiderstand sehr groß: R= 20 Ohm statt 7.45 Ohm: Dadurch haben die
Frequenzgänge „hohe Güte“, also schmale Resonanzkurven der Bandsperre ( Strom ik ) und Bandpass
(Geschwindigkeit vk ) und starke Resonanzüberhöhung beim Tiefpass (Auslenkung xk ).
kg=5,R=20,L=0.006,D=1100,m=0.05,wS=148
0.025
i/10
0.02
i/10
0.015
10*x
x*10
0.01
u0/100
v/10
v/10
0.005
u0/100
0
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
Zeit t
Figur oberhalb: Sprungantworten bei großem Spulenwiderstand (R=20 Ohm statt 7.45 Ohm):
Alle drei Größen Strom i, Geschwindigkeit v und Auslenkung x zeigen Schwingung mit relativ wenig
Dämpfung. (entspricht wieder „hohe Güte“). Jetzt ist die anfängliche „Spitze“ im Stromverlauf zwar noch
erkennbar, aber nicht mehr so auffällig wie bei den anderen früheren Kurven