cl - home.hs-karlsruhe.de

Prof. Dr. R. Kessler, C:\ro\Si05\köller\KabelModell1.doc, S. 1/2
Homepage: http://www.home.hs-karlsruhe.de/~kero0001/
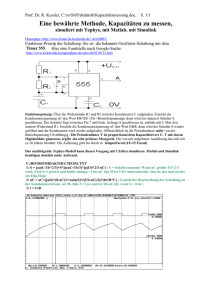
Modell eines Kabels (Leitung), aufgebaut aus verlustloser Kette aus
LCL-T-Gliedern, Quellwiderstand R0, Ausgangswiderstand RA
R0
u0
L1 i1
L
i2
u1 C
C
L
i3
u2 C
L
L
i4
u3
C
u4
L
i5
C
i6
L1
u6
u5 C
i7
uA
RA
Als Modell eines Kabels wird eine Kette aus verlustlosen LCL-T-Gliedern verwendet.
Die Schaltung zeigt eine Kette aus 6 LCL-T-Gliedern. Aufstellen der DGLn:
u0 = R0*i1 +L1*di1/dt + u1 ==>
i1=C*du1/dt+i2
==>
u1=L*di2/dt+u2
==>
usw.
i6 =C*du6/dt +i7
==>
u6= L1*di7/dt + RA*i7
==>
di1/dt = (u0-R0*i1-u1)/L1 ==> i1=i1+ ( u0-R0*i1-u1)*dt/L1
du1/dt = (i1-i2)/C
==> u1=u1+ (i1-i2)*dt/C
di2/dt= (u1-u2)/C
==> i2=i2+ (u1-u2)*dt/L
du6/dt = (i6-i7)/C
di7/dt = (u6 –RA*i7)/L1
==> u6=u6+ (i6-i7)*dt/C
==> i7=i7 + (u6-RA*i7)*dt/L1
Anschließend wird für eine Kette aus 13 solcher LCL-T-Gliedern die Lösung der DGLn programmiert. Als
Eingangsspannung u0 wird ein Sprung von 0 auf 1 zur Zeit tstart und ein Rücksprung auf 0 zur Zeit tstop
angenommen. Es werden nur die Spannungen u1 und uA und die Spannung uM am Kondensator in der Mitte der
Kette geplottet.
Zunächst einige Aufrufe, anschließend die zugehörige Matlab-Datei.
bild 1, R0=1, RA=1, L1=0.5, dt=0.01, tstart=5, tstop=65
4.5
4
3.5
3
2.5
2
uA
1.5
1
uM
0.5
0
u0, u1
-0.5
0
20
40
60
80
100
120
sec
clear; L=1;L1=0.5;C=1;R0=1; RA=1; dt =1e-2;tstart=5; tmax=130;tstop=65; bild=1;cl=1; kabel4
Da hier R0 und RA gleich dem „Wellenwiderstand“ sqrt(L/C) =1 sind, treten keine „Reflexionen“ auf.
Man beachte, dass in diesem Fall (R==1, RA=1) alle drei Spannungen u1, uM und uA maximal den
(stationären) Wert 0.5 erreichen, also nur halbe Quellspannung.
Prof. Dr. R. Kessler, C:\ro\Si05\köller\KabelModell1.doc, S. 2/3
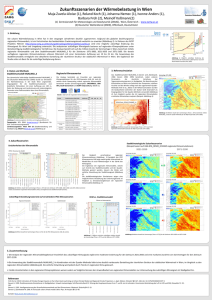
bild 2, R0=1, RA=100, L1=0.5, dt=0.01, tstart=5, tstop=65
4.5
4
3.5
3
2.5
2
uA
1.5
1
uM
0.5
0
u0, u1
-0.5
0
20
40
60
80
100
120
sec
clear; L=1;L1=0.5;C=1;R0=1; RA=100; dt =1e-2;tstart=5; tmax=130;tstop=65; bild=2;cl=1; kabel4
Hier ist RA =100, also hochohmiger Abschluss , folglich wird von Kettenende eine Welle gleicher Phase
reflektiert . Aber am Kettenanfang findet keine Reflexion statt, weil R0=Wellenwiderstand ist (siehe die Kurven
uM und u1 ). Wegen des hochohmigen Abschlusses erreichen alle drei Spannungen u1, uM, uA den
(stationären) Maximalwert 1, also den Wert der Quellspannung u0.
bild 3, R0=1, RA=0, L1=0.5, dt=0.01, tstart=5, tstop=65
4.5
4
3.5
3
2.5
2
uA
1.5
1
um
0.5
0
u0, u1
-0.5
0
20
40
60
80
100
120
sec
clear; L=1;L1=0.5;C=1;R0=1; RA=0; dt =1e-2;tstart=5; tmax=130;tstop=65; bild=3;cl=1; kabel4
Hier ist RA=0, also Kurzschluss am Kettenende. Folglich läuft eine Welle mit Gegenphase zurück, aber sie wird
am Kettenanfang nicht reflektiert, weil R0=Wellenwiderstand ist.
Die zugehörige Matlab-Datei Kabel4.m
% Datei Kabel4.m Simulation eines Kabels.
% Auch Rücksprung bie u0
%Modell: eine Kette von LC-Gliedern in Form von 13 LCL-T-Gliedern
% gleiche Kondensatoren C, gleiche Spulen L, aber die Spulen am Anfang und am Ende sind L1
% Variation Eingangswiderstand R0 und Ausgangswiderstand RA. Sprungantwort gesucht
%clear; L=1;L1=0.5;C=1;R0=1; RA=100; dt =1e-2;tstart=5;tmax=100;tstop=65; bild=1;cl=1; kabel4
% clear; L=1;L1=0.5;C=1;R0=1; RA=100; dt =1e-2;tstart=5; tmax=130;tstop=65; bild=2;cl=1; kabel4
% clear; L=1;L1=0.5;C=1;R0=1; RA=0; dt =1e-2;tstart=5; tmax=130;tstop=65; bild=3;cl=1; kabel4
format compact
Prof. Dr. R. Kessler, C:\ro\Si05\köller\KabelModell1.doc, S. 3/4
Np=floor(tmax/dt); tp=zeros(Np,1); u1p=tp; uMp=tp; uAp=tp; u0p=tp;
%Startwerte:
i1=0; i2=0; i3=0; i4=0; i5=0; i6=0; i7=0; i8=0;i9=0; i10=0; i11=0; i12=0; i13=0;i14=0;
u1=0; u2=0; u3=0; u4=0; u5=0; u6=0; u7=0; u8=0; u9=0; u10=0; u11=0; u12=0;u13=0;
k=0; t=0;
tic
% Numerisches Lösen der DGLn mit dem “Tephys-Algorithmus”
%
der ist viel genauer als der "Euler-Algorithmus", vgl.
% http://www.home.hs-karlsruhe.de/~kero0001/Euler_Tephys/Vergleich%20Euler%20Tephys1.pdf
while t < tmax
u0=1*(t>5)*(tstop>t); % Sprung bei tstart von 0 auf den Wert 1, ab tstop auf 0
i1= i1+(u0-R0*i1-u1)*dt/L1;
u1= u1+ (i1-i2)*dt/C;
i2=i2+(u1-u2)*dt/L;
u2= u2+ (i2-i3)*dt/C;
i3=i3+(u2-u3)*dt/L;
u3= u3+ (i3-i4)*dt/C;
i4=i4+(u3-u4)*dt/L;
u4= u4+ (i4-i5)*dt/C;
i5=i5+(u4-u5)*dt/L;
u5= u5+ (i5-i6)*dt/C;
i6=i6+(u5-u6)*dt/L;
u6= u6+ (i6-i7)*dt/C;
i7=i7+(u6-u7)*dt/L;
u7= u7+ (i7-i8)*dt/C;
i8=i8+(u7-u8)*dt/L;
u8= u8+ (i8-i9)*dt/C;
i9=i9+(u8-u9)*dt/L;
u9= u9+ (i9-i10)*dt/C;
i10=i10+(u9-u10)*dt/L;
u10= u10+(i10-i11)*dt/C;
i11=i11+(u10-u11)*dt/L;
u11= u11+(i11-i12)*dt/C;
i12=i12+(u11-u12)*dt/L;
u12= u12+(i12-i13)*dt/C;
i13=i13+(u12-u13)*dt/L;
u13= u13+(i13-i14)*dt/C;
i14=i14+(u13-RA*i14)*dt/L1;
% Plotwrte speichern:
k=k+1; tp(k)=t; u1p(k)=u1; uMp(k)=u6; u0p(k)=u0;
uAp(k)= RA*i14;
t=t+dt;
end; toc
figure(bild);
if cl>0 clf reset; end; if cl<=0 hold on; end;
ofs=1;
plot(tp,u0p,'k',tp,u1p, tp, uMp+ofs, tp,uAp+2*ofs); grid on
S1=['bild ',num2str(bild)]; S2=[', R0=',num2str(R0)]; S3=[', RA=',num2str(RA)];
S4=[', L1=',num2str(L1)]; S5=[', dt=',num2str(dt)]; S6=[', tstart=',num2str(tstart)];
S7=[', tstop=',num2str(tstop)];
tit=[S1,S2,S3,S4,S5,S6,S7]; title(tit); xlabel('sec');
text(max(tp), 0,' u0, u1'); text(max(tp),ofs,' uM'); text(max(tp),2*ofs,' uA');
axis([0,max(tp),-0.7,4.5]);