Pictures by PC Anleitung zur geometrischen Programmierung am

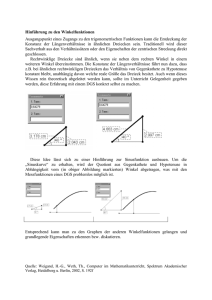
Pictures by PC
Anleitung zur geometrischen
Programmierung am CADEX-Beispiel
Vorbemerkung
Als eine der ersten, praktischen Zeichenübungen unter Pictures by PC nutzten Sie vermutlich die
Lektion
„Einfaches CAD-Beispiel“ (vgl. CADEX.PDF). Darin wurde ein Flansch mit
ausgerundeten Innentaschen entsprechend der Abbildung unten konstruiert.
Um zeichnerisch zu obigem Ergebnis zu gelangen, mußten eine Reihe, interaktiver Manipulationen
vorgenommen werden. An dieser Stelle wollen wir jetzt einmal einen ganz anderen, zugegeben
etwas anspruchsvolleren Weg beschreiben, um die wesentlichen geometrischen Konturen zu
gewinnen. Dazu nutzen wir aber keine interaktive Methode, sondern die Programmiermöglichkeiten
von Pictures by PC. Natürlich wird sich der Aufwand, ein eigenständiges Programm zur
Erzeugung dieses Flansches zu erstellen, nur dann lohnen, wenn damit eine ganze Teilefamilie mit
variierenden Abmessungen generiert werden kann. Wir sprechen in einem solchen Fall von
Variantenkonstruktion oder parametrischer Generierung. Anhand obigen Beispiels wollen wir im
Folgenden schrittweise die geometrische Programmierung unter Pictures by PC erlernen.
Geometrieanalyse
Reduzieren wir zunächst einmal die Geometrie auf das Wesentlichste, bestimmen die notwendigen,
variablen Eingabeparameter und analysieren, welche Punkte für die geometrischen Beschreibung
mit Kreisbogen und Geraden von Bedeutung sind. Werfen wir einmal einen Blick auf die nächste
Abbildung, so erkennen wir, daß die Geometrie des Teils spiegelsymmetrisch zur horizontalen
Verbindungsgeraden durch die beiden Kreiszentren ist. Z.B. sind die x-Koordinaten der Punkte
„pnt1“ und „pnt4“ gleich während die y-Koordinate einmal positiv und einmal negativ ist, sofern
man „cent1“ als Bezugspunkt wählt. Die Berechnung aller Punktkoordinaten dieser Geometrie
reduziert sich also auf ca. die Hälfte aller Punkte. Wenn man zusätzlich weiß, daß unter Pictures by
PC Kreisbogen durch Zentrumskoordinate, Radius und Anfangs- bzw. Endwinkel eindeutig
bestimmt sind, wird verständlich, warum nur Bogenzentren und Geradenendpunkte in der
Zeichnung als Punkte markiert sind. Selbstverständlich wird man zusätzlich die Anfangs- und
Endwinkel der Bogen errechnen müssen. Zur Nomenklatur: Die in der Zeichnung bemaßten Größen
kennzeichnen die Eingabewerte für den Benutzerdialog unseres späteren Programms. Links vom
Gleichheitszeichen („=“) steht der verwendete Variablenname und rechts davon der zugehörige
Benutzerdialog.
Grundsätzlich gibt es für die Lösung geometrischer Aufgabenstellungen häufig mehrere
Möglichkeiten und sehr unterschiedliche Vorgehensweise (z.B. konventionell wie unten, mit Hilfe
von Vektoren oder algebraisch etc.). Wir wählen den konventionellen Ansatz, da er außer einfacher
Winkelfunktionen keine weiteren Kenntnisse voraussetzt.
In der nächsten Abbildung ist schon der erste Lösungsansatz zu erkennen, wie man die Koordinaten
der Punkte „cent2“ sowie „pnt1“, „pnt2“ (in Abhängigkeit vom Winkel „ang“) bezogen auf den
Referenzpunkt „cent1“ ermitteln kann. Dazu sind sicherlich einige Erläuterungen hilfreich, die Sie
anhand der Zeichnung unten nachvollziehen sollten. Ein typisches Kochrezept zur Lösung solcher
oder ähnlicher geometrischer „Probleme“ ist immer, geeignete, rechtwinklige Dreiecke (ggf. aus
Hilfskonstruktionen) zu gewinnen. Dann lassen sich im allgemeinen mittels der Winkelfunktionen
bzw. des Satz des Pythagoras die benötigten Größen ermitteln. In unserem Fall ist als wichtigste
Größe zunächst der Winkel „ang“ zu bestimmen, da die Punktkoordinaten „pnt1“ und „pnt2“ davon
abhängig sind. Wie Sie aus der Abbildung unten ersehen können, ist eine einfache Hilfskonstruktion
recht nützlich. Wenn Sie nämlich parallel zur Tangente (pnt1,pnt2) durch den Kreismittelpunkt
„cent2“ eine Gerade ziehen (Radius rad2 auf Null reduzieren), ergibt sich daraus ein Schnittpunkt
mit der Geraden zwischen „cent1“ und „pnt1“. Dieser Schnittpunkt bildet zusammen mit den
Punkten „pnt1“, „pnt2“ und „cent2“ ein Rechteck. Darunter liegt ein rechtwinkliges Dreieck
zwischen „cent2“, „cent1“ und dem neuen Schnittpunkt. Man kann leicht erkennen, daß darin der
spitze Winkel wieder „ang“ ist. Somit haben wir über die Sinusfunktion folgende Beziehung:
sin(ang)=Gegenkathete/Hypotenuse=(rad1-rad2)/d
In der Abbildung nutzen wir die gleiche Formel nur mit Winkelfunktionen im Gradmaß („sind“
entspricht also „Sinus Degree“ vgl. CAL-Kommando), das erspart uns die Umrechnung vom
Bogenmaß zum Gradmaß und vereinfacht den Ausdruck. Unsere Winkelbeziehung lautet also
sind(ang)=(rad1-rad2)/d
Da wir nicht am Sinus des Winkels, sondern am Winkel „ang“ selbst interessiert sind, ergibt sich
mit der Umkehrfunktion „Arcussinus“ in unserem Fall „asind“ („Arcussinus Degree“) (durch
Substitution) folgender Ausdruck
ang=asind(sind(ang))=asind((rad1-rad2)/d)
Für die Ermittlung der Punktkoordinaten der Punkte „pnt1“, „pnt2“ ist damit die größte Hürde
genommen. Denn die Formeln
xpnt1=sind(ang)*rad1
ypnt1=cosd(ang)*rad1
bzw.
xpnt2=sind(ang)*rad2
ypnt2=cosd(ang)*rad2
ergeben sich einfach aus den Winkelfunktionen (s.o.).
Für die x-Koordinate von „pnt2“ ist eigentlich noch zusätzlich die Verschiebung (Abstand „d“) in
Bezug zu „cent1“ (unserem Bezugspunkt) zu berücksichtigen. Wir haben das der Einfachheit halber
weggelassen, werden die Korrektur allerdings im Programm ausführen.
Damit haben wir für die tangentiale Außenkontur praktisch alle notwendigen Größen berechnet,
denn „pnt4“ ist spiegelsymmetrisch zu „pnt1“, ebenso wie „pnt3“ zu „pnt2“.
Wenden wir uns jetzt der Innenkontur (Taschenkontur) zu. Sie besteht aus 6 Kreisbogen und zwei
Geraden, die einen geschlossenen Konturzug bilden und jeweils tangential in einander übergehen.
Die nächste Abbildung ist eine vergrößerte Darstellung der Kontur im Bereich „cent1“, „pnt5“ und
„pnt9“. Darin suchen wir die kartesischen Koordinaten des Zentrumspunkt „pnt5“ des
Ausrundungsbogens, dessen Anfangs- und Endwinkel sowie die Koordinaten des Startpunktes
„pnt9“ der Geraden.
Im ersten Moment sieht die Zeichnung komplizierter aus, als sie ist. Um die typischen
rechtwinkligen Dreiecke zu erhalten, ziehen wir eine Parallele (mit dem Abstand w+rad5) zur
tangentialen Außenkontur durch den Punkt „pnt5“. Diese Gerade bildet mit der Geraden
(cent1,pnt1) einen rechten Winkel. Wenn man um „cent1“ einen gedachten Kreis mit dem Radius
rad1+rad5 zieht wird unsere soeben gezeichnete Parallele von diesem im Punkt „pnt5“ geschnitten.
Uns interessiert der Winkel „ang3“, der durch die Gerade (cent1, pnt5) und die Horizontale gebildet
wird. Zunächst läßt sich jedoch nur eine Winkelbeziehung mit dem Winkel „ang2“ herstellen. Denn
es gilt:
cosd(ang2)=Ankathete/Hypotenuse=(rad1-w-rad5)/(rad1+rad5)
Mit dem Trick über die Umkehrfunktion „Arcuscosinus“ erhält man den zugehörigen Winkel. Es
gilt:
ang2=acosd(cosd(ang2))=acosd((rad1-w-rad5)/(rad1+rad5))
Der gesuchte Winkel „ang3“ steht jetzt in einfacher Beziehung zu „ang2“ und „ang“, nämlich
ang3=90-(ang2+ang)
Damit ergeben sich auf einfache Weise die kartesischen Koordinaten des Punktes „pnt5“
xpnt5=cosd(ang3)*(rad1+rad5)
ypnt5=sind(ang3)*(rad1+rad5)
Entsprechend unproblematisch ergeben sich die Koordinaten für „pnt9“ in Abhängigkeit von
„pnt5“. Es gilt
xpnt9=xpnt5-(sind(ang)*rad5)
ypnt9=ypnt5+cosd(ang)*rad5
Somit haben wir in diesem Bereich alle für uns wichtigen Größen bestimmt. Das Zentrum „pnt5“
des kleinen Ausrundungskreis mit dem Radius „rad5“, dem Startwinkel (360-ang3) und dem
Endwinkel (90+ang). Ebenso ist die Position des Punktes „pnt9“ als Startpunkt der Geraden
bekannt.
Als nächstes gilt es in analoger Vorgehensweise die Geometrien im Bereich „cent2“, „pnt6“ und
„pnt10“ zu berechnen (s. Abb. unten). Das ist geometrisch im Prinzip nichts Neues. Es bietet sich
also für den Leser die Gelegenheit, das „Problem“ mit den vorgegebenen geometrischen Größen
eigenständig zu lösen und die zugehörigen Formeln aufzustellen.
Der Vollständigkeit halber folgt hier unser Lösungsvorschlag. Um unsere Winkelfunktionen
sinnvoll nutzen zu können, ziehen wir wieder eine Parallele mit dem Abstand (w+rad5) zur
Außentangente. Der Schnittpunkt eines gedachten Kreises um das Zentrum „cent2“ mir dem Radius
(rad2+rad5) und der soeben erzeugten Gerade ergibt den Mittelpunkt „pnt6“ des kleinen
Ausrundungskreises. Für uns ist die Ermittlung des Winkels „ang5“ von Bedeutung, da daraus die
kartesischen Koordinaten des Punktes „pnt6“ (xpnt6,ypnt6) ermittelt werden können. Für den
Winkel „ang4“ können wir über den Cosinus leicht eine Beziehung mit bekannten Größen
aufstellen. Es gilt:
acosd(ang4)=Ankathete/Hypotenuse=(rad2-w-rad5)/(rad2+rad5)
Den Winkel „ang4“ erhalten wir dann aus der Umkehrfunktion Arcuscosinus mit
ang4=acosd(acosd(ang4))=acosd((rad2-w-rad5)/(rad2+rad5))
Der gesuchte Winkel „ang5“ ergibt sich aus der einfachen Beziehung
ang5=90+ang-ang4
Damit sind die Koordinaten der Punkte „pnt6“ und „pnt10“ über die Winkelfunktionen leicht
berechenbar (vgl. Abb.).
Bedenken Sie aber, daß sich unsere Formeln relativ auf das Zentrum „cent2“ beziehen. In unserem
späteren Programm berücksichtigen wir natürlich die Verschiebung zum eigentlichen Bezugspunkt
„cent1“. Betrachten wir jetzt noch die Spiegelsymmetrie zur Linie (cent1,cent2), so haben wir die
Geometrie unseres Flansches komplett bestimmt und können mit der Programmierung beginnen.
Dabei wollen wir didaktisch so vorgehen, daß wir zunächst mit einer sehr einfachen aber
funktionellen Prozedur CADEX1.PRC beginnen, diese dann zur Version CADEX.PRC verbessern
und schließlich eine optimale Basic-Variante CADEX.BIX mit grafischem Benutzerdialog
generieren. Die genannten Prozeduren und Module dienen der Programmierausbildung und sind
entsprechend umfangreich kommentiert. Natürlich sollte der Leser zur Kommandoanalyse ständig
auf den Referenzteil der Pictures by PC Benutzerhilfe zurückgreifen.
In dieser begleitenden Lektion werden wir lediglich prinzipielle Erläuterungen zu den genannten
Prozeduren und Modulen machen. Beginnen wir jetzt mit der Prozedur CADEX1.PRC.