Brückenkurs Schulmathematik 8. Veranstaltung: Geometrie 4

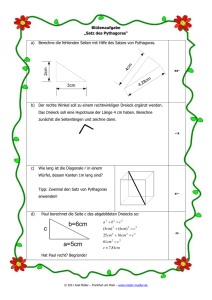
Brückenkurs Schulmathematik
8. Veranstaltung: Geometrie 4: Dreiecke
03. Juli 2013
1. Dreieckskonstruktionen, Kongruenzsätze
1. Aufgabe: Konstruieren Sie, falls möglich, ein passendes Dreieck ABC mit Zirkel und
Lineal! Sind alle konstruierbaren Dreiecke kongruent? Formulieren Sie anhand Ihrer
Erfahrungen Kongruenzsätze für Dreiecke!
a.
a = 3 cm, b = 4 cm, c = 6 cm
b. a = 3 cm, b = 4 cm, γ = 30°
c. a = 3 cm, b = 4 cm, α= 30°
d. a = 3 cm, b = 4 cm, β=30°
e. a = 5 cm, β=30°, γ = 45°
f. a = 5 cm, α=30°, γ = 45°
g. α=30°, β=105°, γ = 45°
2. Aufgabe: Denken Sie sich jeweils drei Größen eines Dreiecks aus, zu denen man kein
Lösungsdreieck konstruieren kann, und zwar in den folgenden Kombinationen:
a. drei Seiten
b. zwei Seiten und ein Winkel
c. eine Seite und zwei Winkel.
Begründen Sie, warum es zu den Angaben kein entsprechendes Dreieck existiert.
2. Ähnlichkeit von Dreiecken
3. Aufgabe: Mit Ähnlichkeit und ähnlichen Figuren haben wir uns bereits beschäftigt. Daher
wissen wir schon, dass zwei Dreiecke zueinander ähnlich sind, wenn es eine
Ähnlichkeitsabbildung gibt, die das eine Dreieck dem anderen zuordnet.
a. Zeichnen Sie zwei ähnliche Dreiecke! Was kann man über ihre Seiten und
Winkel behaupten?
b. Formulieren Sie anhand Ihrer Erfahrungen Ähnlichkeitssätze für Dreiecke!
c. Vergleichen Sie diese Sätze mit den Kongruenzsätzen für Dreiecke! Was fällt
Ihnen auf?
3. Satzgruppe des Pythagoras
6. Aufgabe: Formulieren Sie den Satz des Pythagoras!
7. Aufgabe: Für diesen Satz sind mehrere hundert Beweise bekannt. Ein klassischer Beweis,
der oft in der Schule behandelt wird, arbeitet mit Flächenumwandlung. Rekapitulieren Sie
diesen Beweis!
8. Aufgabe: Ein weiterer Beweis geht aus der Tatsache aus, dass bei der Errichtung der
Höhe zur Hypotenuse insgesamt drei zueinander ähnliche Dreiecke entstehen. Zeigen Sie
mithilfe dieser ähnlichen Dreiecke den Satz des Pythagoras! Welche anderen
Zusammenhänge sind dabei als „Nebenprodukt“ bewiesen worden?
9. Aufgabe: Sind Ihnen weitere Beweise für den Satz des Pythagoras bekannt? Zeigen Sie
diese!
10. Aufgabe: Der Höhensatz und die Kathetensätze können ebenfalls durch
Flächenumwandlung bewiesen werden. Hinweis: Um diese durchzuführen brauchen Sie
die Seiten eines rechtwinkligen Dreiecks geschickt zu wählen. Zeigen Sie den Höhensatz
und die Kathetensätze durch Flächenumwandlung!
11. Aufgabe: Zeigen Sie mithilfe des Höhensatzes, wie man ein beliebiges Rechteck in ein
flächengleiches Quadrat umwandeln kann!
12. Aufgabe: Formulieren Sie die Umkehrung des Satzes des Pythagoras! Wie könnte man
die Gültigkeit dieser Aussage zeigen?
13. Aufgabe: Der Satz des Pythagoras lässt sich auf ähnliche Figuren über die Seiten eines
rechtwinkligen Dreiecks verallgemeinern. Dies bedeutet, dass es für den Flächeninhalt
ähnlicher Figuren, die über die Seiten eines rechtwinkligen Dreiecks errichtet werden, gilt,
dass die Summe der Flächeninhalte der Figuren über den Katheten gleich dem
Flächeninhalt der Figur über der Hypotenuse ist. Beweisen Sie diesen Satz mithilfe der
Ähnlichkeit!
14. Aufgabe: Zeichnen Sie über den Seiten a, b, c eines rechtwinkligen Dreiecks die
jeweiligen Halbkreise Ha,Hb,Hc “nach oben”, d.h. Hc durch die Spitze C des Dreiecks. Die
Flächen Ma und Mb zwischen den Halbkreisen über den Katheten und Hc heißen
Möndchen des Hippokrates.
Zeigen Sie mithilfe des verallgemeinerten Satzes des Pythagoras: Die Summe der
Flächeninhalte der Möndchen ist dem Flächeninhalt des rechtwinkligen Dreiecks gleich!
15. Aufgabe: Pythagoreische Zahlentripel sind solche ganze Zahlen, die die Seitenlängen
eines rechtwinkliges Dreiecks darstellen können, also solche Tripel aus ganzen Zahlen,
für die gilt, dass die Quadratsumme von zwei Zahlen dem Quadrat der dritten Zahl
entspricht. Das bekannteste (und einfachste) solche Tripel besteht aus den Zahlen 3, 4
und 5.
a. Kennen Sie weitere pythagoreische Zahlentripel? Zeigen Sie, dass für diese Zahlen der
gewünschte Zusammenhang gilt!
b. Ein allgemeines Verfahren ist bis heute nicht bekannt, nach dem man alle
pythagoreischen Zahlentripel erzeugen könnte. Es gibt allerdings Methoden, die
pythagoreische Zahlentripel erzeugen. Recherchieren Sie nach solchen Verfahren
und versuchen Sie zu begründen, warum die jeweilige Methode geeignet ist,
Zahlentripel mit der gewünschten Eigenschaft zu liefern!