Kap. 10 (Teil I) Stichproben

Bei der Sammlung von Daten, die bestimmte Merkmale einer Gruppe von Objekten
betreffen, wie z.B. Alter der Studenten einer Universität oder die Anzahl der defekten und
nicht defekten Bolzen der Tagesproduktion einer Fabrik, ist meistens unmöglich oder
unpraktisch, die gesamte Gruppe, bezeichnet als Grundgesamtheit (Population), zu
untersuchen. Stattdessen beschränkt man sich auf einen kleinen Teil der Gruppe, genannt
Stichprobe.
Eine Grundgesamtheit kann endlich oder unendlich sein. So ist z.B. die Grundgesamtheit
aller an einem Tag produzierten Bolzen endlich, Dagegen ist die Grundgesamtheit aller
möglichen Ergebnisse (Wappen, Zahl) aufeinanderfolgenden Würfen einer Münze
unendlich.
Eine endliche Grundgesamtheit kann theoretisch als eine unendliche Grundgesamtheit
aufgefasst werden, wenn eine Stichprobenentnahme durch das Ziehen mit Zurücklegen
geschieht. Für viele praktische Zwecke kann die Entnahme von Stichproben aus einer sehr
großen Grundgesamtheit als eine Stichprobenentnahme aus einer unendlichen
Grundgesamtheit angesehen werden.
Die Schätzung der unbekannten Quantitäten der Grundgesamtheit, wie z.B. der Mittelwert
und die Varianz, die häufig als Parameter der Grundgesamtheit bezeichnet werden, erfolgt
auf der Grundlage der Kenntnisse über die Quantitäten einer Stichprobe, welche häufig
Stichproben-Statistiken genannt werden.
Damit die statistischen Schlussfolgerungen anhand der Stichprobe gültig sind, müssen die
Stichproben so gewählt werden, dass sie repräsentativ für die Grundgesamtheit sind. Eine
Stichprobenentnahme vom Umfang N Elemente aus der Grundgesamtheit kann bewusst
oder zufällig geschehen.
Grundgesamtheit (Population)
Parameter: µ ; σ
Stichprobe
Statistiken: X
; S
1
Zufallsstrichprobe
Eine ZufallsStrichprobe vom Umfang N , deren Elemente zufällig aus einer
Grundgesamtheit entnommenen wurden, ist eine Folge von unabhängigen und identischen
verteilten Zufallsvariablen:
X1; X2; ... ;XN
Dabei ist X i die Merkmalausprägung des i-ten Elements der Strichprobe. Die X i heißen
Stichprobenvariablen.
Nur im Falle einer unendlichen Grundgesamtheit sind die X i wirklich unabhängig und
identisch verteilt. Denn das Ziehen eines Elements aus der Grundgesamtheit den Rest der
Grundgesamtheit nicht beeinflusst. Für endlichen Grundgesamtheiten setzen wir voraus,
dass die Anzahl der Elemente der Grundgesamtheit sehr groß ist, so dass das Ziehen
eines Elements die Grundgesamtheit sehr wenig ändert.
!
Die Schätzung der unbekannten Quantitäten der Grundgesamtheit, wie z.B. der Mittelwert
und die Varianz, die häufig als Parameter der Grundgesamtheit bezeichnet werden, erfolgt
auf der Grundlage der Kenntnisse über die Quantitäten einer Stichprobe, welche häufig
Stichproben-Statistiken oder Schätzfunktionen genannt werden.
Gesamtheit
Stichprobe:
Statistiken
(Kenngrößen
der Stichprobe)
Mittelwert
Schätzen der
Parameter
(Kenngrößen
der Gesamtheit)
Mittelwert
2
Stichproben-Statistiken:
Seien X 1 ; X 2 ; . . . ; X N die Zufallsvariablen einer Stichprobe vom Umfang N.
Der Mittelwert dieser Stichprobe ist:
X =
N
1
Xi
⋅
N
i = 1
Die Varianz dieser Stichprobe ist:
S2 =
N
1
N − 1
( Xi
⋅
− X
)2
i = 1
"
Möchte man den Mittelwert oder Varianz einer konkreten Stichprobe berechnen, so setzt
man für die Zufallsvariablen, die jeweiligen Werte x 1 ; x 2 ; . . . ; x N aus der konkrete
Stichprobe ein.
Parameter der Grundgesamtheit:
Seien x 1 ; x 2 ; . . . ; x NG die einzelnen Elemente einer Gesamtheit der Größe NG.
Der Mittelwert dieser Gesamtheit ist:
µ =
1
NG
NG
xi
⋅
i = 1
Die Varianz dieser Gesamtheit ist:
σ
#
$
2
%
=
1
NG
NG
⋅
(
xi − µ
)2
&
'
i = 1
Betrachten wir alle möglichen Stichproben vom Umfang N aus einer Grundgesamtheit
der Größe NG , so können wir für jede Stichprobe Statistiken, wie den Mittelwert X
berechnen. Diese Werte unterscheiden sich natürlich von Stichprobe zu Stichprobe. Auf
diese Weise erhalten wir eine Verteilung der statistischen Werte für die verschiedenen
Stichproben, die als Stichprobenverteilung von X bezeichnet wird.
Theorem
Sei µ der Mittelwert (Erwartungswert) einer Grundgesamtheit.
Und sei µ
X
der Mittelwert aus den Mittelwerten von Stichproben vom Umfang N aus
der Grundgesamtheit, dann gilt für den Mittelwert der Verteilung der StichprobenMittelwerte:
µ
= µ
X
3
Eine Universität hat 4 Studenten (Grundgesamtheitsgröße: NG = 4 ). Die Noten der 4
Studenten sind jeweils 1 ; 2 ; 3 bzw. 4 .
Berechnen Sie den Mittelwert der Grundgesamtheit.
Es sollen Stichproben vom Umfang N = 2 mit Zurücklegen entnommen werden. Geben
Sie alle möglichen Stichproben an.
Berechnen Sie den Mittelwert der Stichproben-Mittelwerte.
Verifizieren Sie das obige Theorem, indem Sie das Ergebnis aus a) mit dem aus c)
vergleichen.
()
"
Gesamtheit: { 1 ; 2 ; 3 ; 4 } ; NG = 4
µ
=
1
NG
NG = 4
NG
xi
⋅
1
==
4
i = 1
( 1 + 2 + 3 + 4 ) = 2,5
Alle möglichen verschiedenen Stichproben vom Umfang N = 2 lauten:
1
{1;1}
{2;1}
{3;1}
{4;1}
1
2
3
4
2
{1;2}
{2;2}
{3;2}
{4;2}
3
{1;3}
{2;3}
{3;3}
{4;3}
4
{1;4}
{2;4}
{3;4}
{4;4}
Die Mittelwerte der jeweiligen 16 Stichproben sind:
x
x
x
x
=
=
=
=
1
1,5
2
2,5
x
x
x
x
=
=
=
=
1,5
2
2,5
3
x
x
x
x
=
=
=
=
2
2,5
3
3,5
x
x
x
x
=
=
=
=
2,5
3
3,5
4
Folglich ist der Mittelwert der Stichproben-Mittelwerte:
µ
X
1
⋅ [ 1 ⋅ ( 1 ) + 2 ⋅ ( 1, 5 ) + 3 ⋅ ( 2 ) + 4 ⋅ ( 2 , 5 ) + 3 ⋅ ( 3 ) + 2 ⋅ ( 3 , 5 ) + 1 ⋅ ( 4 ) ]
16
= 2,5
=
µ
X
= 2,5 = µ
4
#
$
%
&
'
σ
Theorem
Sei
² die Varianz einer Grundgesamtheit.
Und sei σ
2
die Varianz der Mittelwerte von Stichproben vom Umfang N aus der
X
Grundgesamtheit.
Wenn die Stichprobenentnahme mit Zurücklegen erfolgt oder bei einer Entnahme ohne
Zurücklegen die Grundgesamtheit unendlich oder sehr groß im Vergleich zum Umfang
der entnommenen Stichprobe ist, gilt für die Varianz bzw. Standardabweichung der
Verteilung der Stichproben-Mittelwerte:
σ
2
=
X
σ
2
N
;
σ
X
=
σ
N
Bearbeiten Sie folgende Teilaufgaben für das vorige Bespiel.
Eine Universität hat 4 Studenten (Grundgesamtheitsgröße: NG = 4 ). Die Noten der 4
Studenten sind jeweils 1 ; 2 ; 3 bzw. 4 .
Berechnen Sie die Varianz der Grundgesamtheit.
Berechnen Sie die Varianz der Stichproben-Mittelwerte.
Verifizieren Sie das obige Theorem, indem Sie das Ergebnis aus a) mit dem aus c)
verwenden.
()
"
Gesamtheit: { 1 ; 2 ; 3 ; 4 } ; NG = 4
µ
σ
1
=
2
=
NG
=
1
4
1
NG
[
NG
xi
⋅
= 2,5
i = 1
NG
⋅
(xi
− µ
)2
i = 1
⋅ (1 − 2 ,5 ) 2 + ( 2 − 2 ,5 ) 2 + ( 3 − 2 ,5 ) 2 + ( 4 − 2 ,5 ) 2
] = 1, 25
5
Die Mittelwerte der jeweiligen 16 Stichproben sind:
x
x
x
x
=
=
=
=
x
x
x
x
1
1,5
2
2,5
=
=
=
=
x
x
x
x
1,5
2
2,5
3
=
=
=
=
x
x
x
x
2
2,5
3
3,5
=
=
=
=
2,5
3
3,5
4
Der Mittelwert der Verteilung der Stichproben-Mittelwerte ist:
µ
X
= 2,5
Die Varianz der Verteilung der Stichproben-Mittelwerte ist:
σ
2
X
1
=
16
1
=
16
16
⋅
( x i − µ x )2
i = 1
⋅ [ 1 ⋅ ( 1 − 2 , 5 ) 2 + 2 ⋅ ( 1, 5 − 2 , 5 ) 2 + 3 ⋅ ( 2 − 2 , 5 ) 2 + 4 ⋅ ( 2 , 5 − 2 , 5 ) 2
+ 3 ⋅ ( 3 − 2,5 )
µ
X
= 2,5 = µ
2
;
+ 2 ⋅ ( 3,5 − 2,5 ) 2 + 1⋅ ( 4 − 2,5 ) 2
σ
2
= 0 , 625 =
X
σ
2
N
=
]
1 , 25
2
= 0 , 625
= 0 , 625
* +
Ergänzen Sie folgende Tabellen für die Wahrscheinlichkeitsverteilung der Noten aus
der Gesamtheit und der Stichproben- Mittelwerte der Noten für Stichproben vom
Umfang N = 2 aus dem vorigen Beispiel.
Zeichnen Sie die Wahrscheinlichkeitsverteilung für die beiden Verteilungen.
()
"
X
P(X
)
X
P X
( )
X
P(X )
X
P X
( )
1
1 4
2
1 4
1
1,5
2
1 16
2 16
3 16
1
1 4
2
1 4
3
1 4
4
1 4
1
1,5
2
2,5
3
3,5
4
1 16
2 16
3 16
4 16
3 16
2 16
1 16
6
f(X)
Verteilung der Grundgesamtheit
f(X)
¼0.25
0.25
0.2
0.2
0.15
0.15
0.1
0.1
0.05
0.05
0
11
22
33
44
X
Stichprobenverteilung von Mittelwerten X
für Stichproben der Größe N = 2
1
1
1.5
1,5
22
2.5
2,5
33
3.5
3,5
44
X
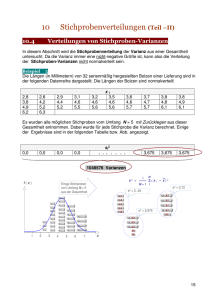
Die Lebensdauern von 40 elektronischen Bauteilen der Grundgesamtheit einer Lieferung
sind in der folgenden Datenreihe dargestellt.
0,2
1,5
2,7
4,8
0,3
1,6
2,78
5,0
0,4
1,72
3,1
5,8
0,55
1,8
3,2
5,99
xi
0,8
1,92
3,96
6,7
0,6
1,9
3,8
6,0
0,84
2,0
4,1
7,0
1,0
2,1
4,32
7,4
1,2
2,35
4,5
8,6
1,45
2,5
4,65
9,4
Es wurden alle möglichen Stichproben vom Umfang N = 2 mit Zurücklegen aus dieser
Gesamtheit entnommen. Dabei wurde für jede Stichprobe der Mittelwert der Lebensdauer
der beiden Dioden gemessen und notiert. Einige der 1600 Ergebnisse sind wie folgt:
__
0,2
0,25
0,25
xi
. . . . . . .
0,3
9,0
9,0
9,4
1600 Mittelwerte
f ( x)
x = 0,9
x = 1,45
0,3
Einige
Stichproben
vom Umfang
N = 2 aus
der Population
x = 0,5
x = 1,75
x = 4,6
x = 2,4
x
x = 7,2
1
3
5
7
x = 7,8
9
7
Die Messdaten der Grundgesamtheit liefern eine Exponentialverteilung. Die Verteilung der
Stichproben-Mittelwerte liefert für Stichproben der Größe N = 2 eine NichtNormalverteilung, dagegen ist die Verteilung der Stichproben-Mittelwerte für Stichproben
der Größe N = 30 (oder größer als 30) annähernd normalverteilt.
f(x)
0.2
0.15
0.1
!
f(x)
0.05
"#
x
0.3
0
0.25
2
2
4
6
6
4
88
10
10
0.2
0.15
0.1
f(x)
0.05
x
00
22
44
66
8
8
10
10
!
0.2
12
0.15
0.1
0.05
x
0
2
2
4
4
66
88
10
10
Vergrößert man den Umfang der jeweiligen Stichproben, so nähert sich die
Wahrscheinlichkeitsverteilung der Mittelwerte der Stichproben aus der
exponentialverteilten Grundgesamtheit, einer Gaußschen Normal-Verteilung.
Satz: Zentraler Grenzwertsatz
Sei X der Mittelwert einer Stichprobe der Größe N aus einer Grundgesamtheit mit dem
Mittelwert µ und der Varianz ² . Für die standardisierte Zufallsvariable
Z =
X − µ
σ
N
gilt dann, dass die Verteilung von Z gegen die Standard-Normalverteilung strebt, wenn
N
∞ strebt.
8
"
Bei großen Werten N (N 30) des Umfangs der Stichproben, entspricht die Verteilung
der Stichproben-Mittelwerte unabhängig von der Verteilung der Grundgesamtheit
ungefähr einer Normalverteilung mit dem Mittelwert µ
und der Varianz σ 2 .
X
X
Falls die Verteilung der Grundgesamtheit eine Normalverteilung ist, so ist die
Stichproben-Verteilung der Mittelwerte schon für kleine Stichprobenumfänge N
(d.h. N 30) eine Normalverteilung.
9
* +
Eine Universität hat 4 Studenten (Grundgesamtheit NG = 4 ). Die Noten der 4 Studenten
sind jeweils 1 ; 2 ; 3 bzw. 4 . (s. Bsp. 1). Es werden aus dieser Gesamtheit alle
möglichen Stichproben vom Umfang N = 36 mit Zurücklegen entnommen.
Geben Sie die Anzahl aller möglichen unterschiedlichen Stichproben an.
Welche der folgenden Verteilungen gibt die Verteilung der Stichproben-Mittelwerte
richtig an?
f(X)
Verteilung der Grundgesamtheit
µ = 2,5
¼
0
1
1
22
σ = 1,118
33
44
X
N = 36
Verteilung von Stichproben-Mittelwerten X
für Stichproben der Größe N = 36
f(x )
µ x = 2,5
Verteilung von Stichproben-Mittelwerten X
für Stichproben der Größe N = 36
f(x )
µ x = 1,5
σ x = 0,186
σ x = 0,186
1,5
x
x
2,5
$
Verteilung von Stichproben-Mittelwerten X
für Stichproben der Größe N = 36
f(x )
µ x = 2,5
Verteilung von Stichproben-Mittelwerten X
für Stichproben der Größe N = 36
f(x )
µ x = 2,5
σ x = 0,186
2,5
σ x = 1,118
x
2,5
x
10
#
Eine Universität hat 4 Studenten. Die Noten der 4 Studenten sind jeweils 1 ; 2 ; 3 bzw. 4 .
(s. Bsp.1 ). Der Mittelwert und die Varianz der Gesamtheit betragen 2,5 bzw. 1,25. Würde
man eine Stichprobe vom Umfang N = 36 entnehmen, wie groß ist dann die
Wahrscheinlichkeit, dass der Mittelwert dieser Stichprobe geringer als 2,85 liegt.
()
"
Gesamtheit: { 1 ; 2 ; 3 ; 4 }
σ ² = 1,25
µ = 2,5 ;
; σ = 1,118
Da N 30 muss die Verteilung der Stichproben-Mittelwerte X eine Normalverteilung mit
µ X = 2,5 und σ 2X = σ 2 N = 1,25 36 = 0,0347 sein.
f(X)
Verteilung der Grundgesamtheit
µ = 2,5
¼
0.25
σ = 1,118
0.2
Verteilung der Stichproben-Mittelwerte
f(x )
Stichproben
0.15
-größen:
N = 36
0.1
µ x = µ = 2,5
1,118
σ
=
σ x=
N
36
0.05
x
0
11
22
33
44
X
2
4
x80 = 2,85
10 12
6
StandardNormalVerteilung
(z)
Z =
14
X – µ
σ
N
z
0
z0
Also ergibt sich für die standardisierte Zufallsvariable
z0
=
x0 − µ
σ
2 , 85 − 2 , 5
=
0 , 186
N
= 1 , 88
Somit ergibt sich:
P
(X
≤ 2 , 85
)
P ( Z ≤ 1, 88
=
=
Φ ( 1, 88
)
)
=
0 , 9699
Also haben 96,99% aller Stichproben einen Stichproben-Mittelwert geringer als 2,85.
11
* +
Sei die Länge von Bolzen einer Lieferung eine normalverteilte Zufallsvariable und sei die
mittlere Länge der Bolzen µ = 7,05 [mm] und die Standardabweichung σ = 3 [mm]. Würde
man eine Stichprobe vom Umfang N = 5 entnehmen, wie groß ist dann die
Wahrscheinlichkeit, dass man eine Stichprobe erhält, deren Mittelwert für die Länge der
Bolzen kleiner als 9 [mm] ist?
()
"
Verteilung der Stichproben-Mittelwerte
Verteilung der Grundgesamtheit
0.25
0.175
0.15
f(x)
Stichprobengröße:
N=5
0.125
σ =3
0.1
0.075
0.2
f(x)
µ x = µ = 7,05
σ
σ x=
0.15
=
3
5
N
0.1
0.05
0.05
0.025
x
2
4
6
µ = 87,0510
12
14
x
Da die Gesamtheit normalverteilt ist, ist die Verteilung
der Stichproben-Mittelwerte aus dieser Gesamtheit
auch bei Stichprobengrößen N = 5 normalverteilt:
x0 − µ
9 − 7 , 05
z0 =
=
= 1 , 45
3
σ
N
5
2
4
6
x
80 = 910
14
StandardNormalVerteilung
(z)
Z =
12
X – µ
σ
N
z
(
P X ≤ 9
)
= P ( Z ≤ 1, 45 ) = 0 , 9265
0 z0
12
#
$
%
&
'
σ
In den Beispielen des vorigen Abschnitts waren neben dem Mittelwert µ auch die
Standardabweichung σ der Grundgesamtheit bekannt. Wenn aber σ einer
normalverteilten Gesamtheit unbekannt ist, kann diese Größe für die standardisierte
X − µ
durch die Standardabweichung s der Stichprobe
Zufallsvariable Z =
σ
N
ersetzt werden. In diesem Fall gehorcht aber die Zufallsvariable T =
X −µ
S
nicht mehr
N
der Standard-Normalverteilung, sondern der Studentschen-t-Verteilung.
Theorem
Seien X und S der Mittelwert bzw. Standardabweichung einer Stichprobe der Größe
N aus einer normalverteilten Grundgesamtheit mit dem Mittelwert µ und der Varianz
² . Dann folgt die standardisierte Zufallsvariable:
X −µ
T =
S
N
einer Studentschen-t-Verteilung mit ν = N – 1 Freiheitsgeraden.
Mit wachenden Freiheitsgeraden ν strebt die Dichtefunktion der t-Verteilung gegen
die der Standard-Normalverteilung. Daher kann für einen Stichprobenumfang von N
30 mit einer ausreichenden Genauigkeit die t-Verteilung durch die StandardNormalverteilung ersetzet werden.
Im Anhang befindet sich eine Tabelle mit den Werten der Verteilungsfunktion F ν ( t )
der Student-t-Verteilung für beliebige t > 0.
$
%
& &
f
ν
(t)
ν = ∞
ν = 10
ν = 3
t
0
13
,
Sei die Länge von Bolzen einer Lieferung eine normalverteilte Zufallsvariable und sei die
mittlere Länge der Bolzen µ = 7,05 [mm] bekannt aber σ unbekannt, wie groß ist dann die
Wahrscheinlichkeit, dass man eine Stichprobe vom Umfang N = 5 erhält, deren Varianz
s² = 4, 2 ist und ihr Mittelwert für die Länge der Bolzen kleiner als 9 [mm] ist?
()
"
Anzahl der Freiheitsgeraden:
ν=N–1 = 5–1=4
Also ergibt sich mit x 0 = 9 und s 0 =
s 02 =
4 , 2 = 2 , 05
für die
standardisierte Zufallsvariable:
t0 =
x0 − µ
=
s0
9 − 7 , 05
2 , 05
2,13
5
N
Also ist die Wahrscheinlichkeit:
P
(X
≤ 9
)
=
P ( T ≤ 2 , 13
) = F 4 ( 2 , 13 ) ≈ 0 , 95
14