B ⊆ AB ist Teilmenge von A Jedes Element von B gehört

Hochschule für Technik, Wirtschaft und Kultur Leipzig
Vorkurs Mathematik 2013
Mengenlehre:
Mengenrelationen und -operationen
Teilmengenrelationen:
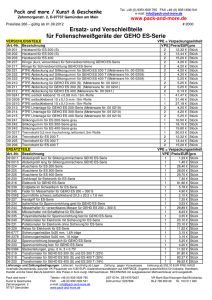
B ⊆ A B ist Teilmenge von A
Jedes Element von B gehört auch zu A.
B ⊂ A B ist echte Teilmenge von A Jedes Element von B gehört auch zu A.
Aber A und B sind nicht gleich.
A = B A und B sind gleich
B⊆A ∧ A⊆B
Mengenoperationen:
Ω Obermenge, A, B ⊆ Ω
Symbol Bezeichnung
Definition
A ∩ B Durchschnitt von A und B A ∩ B = {x : x ∈ A ∧ x ∈ B}
alle Elemente, die zu A und B gehören
A ∪ B Vereinigung von A und B A ∪ B = {x : x ∈ A ∨ x ∈ B}
alle Elemente, die zu A oder B gehören
A
Komplement von A bez. Ω A = {x ∈ Ω : x 6∈ A}
alle Elemente von Ω, die nicht zu A gehören
A\B
Differenz von A und B
A \ B = {x ∈ A : x 6∈ B} = A ∩ B
alle Elemente von A, die nicht zu B gehören
Häufig verwendete Mengen:
R
N
Z
Q
Menge
Menge
Menge
Menge
der
der
der
der
reellen Zahlen
natürlichen Zahlen N = {1, 2, 3, . . .}
ganzen Zahlen
Z = {. . . , −2, −1, 0, 1, 2, . . .}
rationalen Zahlen Q = { pq : p ∈ Z ∧ q ∈ N}
für a, b ∈ R, a < b:
[a, b]
(a, b)
[a, b)
(a, b]
abgeschlossenes Intervall
offenes Intervall
rechtsseitig halboffenes Intervall
linksseitig halboffenes Intervall
[a, b] = {x ∈ R
(a, b) = {x ∈ R
[a, b) = {x ∈ R
(a, b] = {x ∈ R
:
:
:
:
a ≤ x ≤ b}
a < x < b}
a ≤ x < b}
a < x ≤ b}