Trigonometrie: Bergwanderung

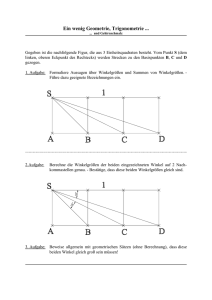
Trigonometrie
In den Bergen unterwegs
Arbeitsblatt
Eine Wandergruppe befindet sich auf einer Schutzhütte und plant eine Rundwanderung. Von der Hütte führt
ein gleichmäßig ansteigender Bergrücken zur Wetterkanzel, einem Aussichtspunkt. Von dort kann die
Kreuzspitze direkt über einen weiteren Bergrücken erreicht werden. Von diesem Gipfel führt wiederum ein
gleichmäßig abfallender Hang zur Hütte zurück. Um die Länge der Runde zu ermitteln, liest die Bergführerin
die Seehöhen in ihrer Wanderkarte ab:
Schutzhütte 1644 m, Wetterkanzel 1997 m, Kreuzspitze 2253 m
Außerdem ermittelt sie aus den entsprechenden Strecken in der Karte die horizontalen Entfernungen von
der Schutzhütte zur Wetterkanzel (ca. 1190 m) bzw. von der Schutzhütte zur Kreuzspitze (ca. 760 m).
Diese beiden Strecken schließen einen rechten Winkel ein.
a)
b)
c)
d)
Wie groß ist die horizontale Entfernung zwischen Kreuzspitze und Wetterkanzel? Messt die
Strecke ab.
Berechnet die Längen der drei Teilstrecken der Wanderung, wenn die Wege geradlinig
verlaufen. Kontrolliert durch Messung. Gebt die Gesamtlänge des Rundweges an.
Ermittelt die Winkel, in denen die beiden Bergrücken bzw. der Hang ansteigen. Gebt
jeweils die Steigung in Prozent an.
Um welchen Winkel muss sich ein Bergsteiger auf der Kreuzspitze drehen, wenn er seinen
Blick von der Wetterkanzel zur Schutzhütte wandern lässt?
Voraussetzungen:
•
•
•
Lehrsatz von Pythagoras
Winkelfunktionen im rechtwinkligen Dreieck
Berechnung der Steigung in Prozent
Bastelanleitung für das Faltmodell:
•
•
•
•
•
Drucke die Grafik in Originalgröße aus.
Klebe sie eventuell auf Karton auf.
Schneide sie entlang der Umrisse aus.
Durch Aufklappen erhältst du das 3D-Modell.
Wenn du an passender Stelle an den strichlierten Linien Schlitze einschneidest, kannst du die Laschen
durchstecken und an der Rückseite festkleben.
Modell im Maßstab: 1 : 10 000
© 2009 Verlag E. DORNER, Wien
Dimensionen – Mathematik 5
1
Trigonometrie
Faltmodell
© 2009 Verlag E. DORNER, Wien
Dimensionen – Mathematik 5
2