Klausur - Jens Münkers Homepage

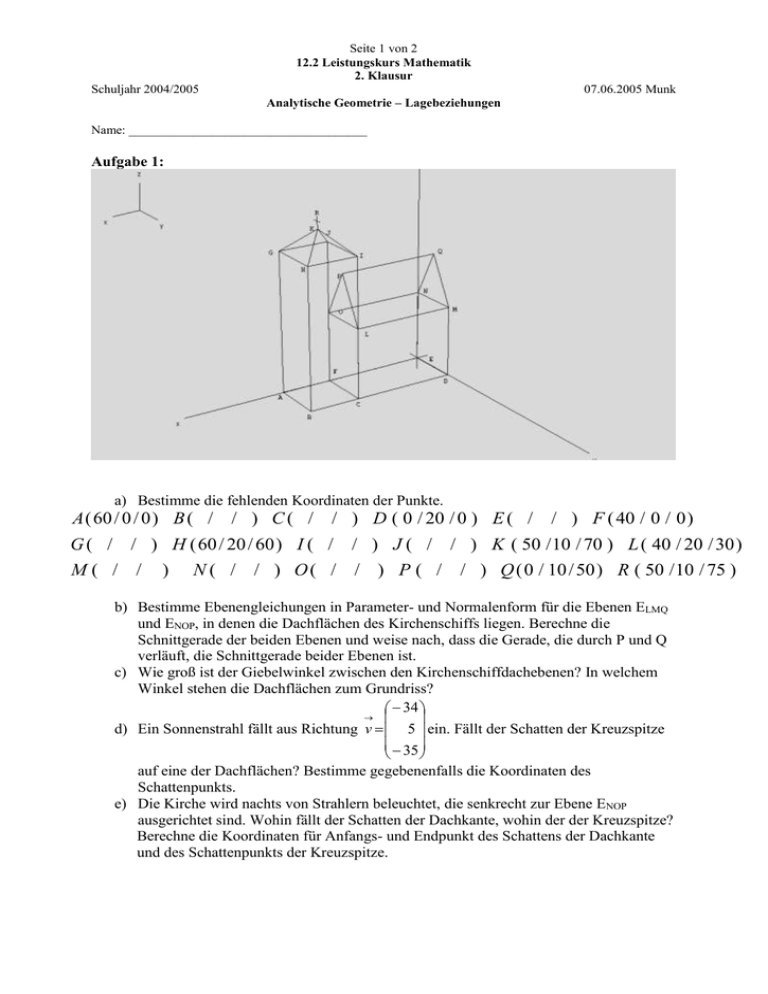
Seite 1 von 2
12.2 Leistungskurs Mathematik
2. Klausur
Schuljahr 2004/2005
07.06.2005 Munk
Analytische Geometrie – Lagebeziehungen
Name: _____________________________________
Aufgabe 1:
a) Bestimme die fehlenden Koordinaten der Punkte.
A ( 60 / 0 / 0 ) B ( / / ) C ( / / ) D ( 0 / 20 / 0 ) E ( / / ) F ( 40 / 0 / 0 )
G ( / / ) H ( 60 / 20 / 60 ) I ( / / ) J ( / / ) K ( 50 / 10 / 70 ) L ( 40 / 20 / 30 )
M( / /
)
N ( / / ) O ( / / ) P ( / / ) Q ( 0 / 10 / 50 ) R ( 50 / 10 / 75 )
b) Bestimme Ebenengleichungen in Parameter- und Normalenform für die Ebenen ELMQ
und ENOP, in denen die Dachflächen des Kirchenschiffs liegen. Berechne die
Schnittgerade der beiden Ebenen und weise nach, dass die Gerade, die durch P und Q
verläuft, die Schnittgerade beider Ebenen ist.
c) Wie groß ist der Giebelwinkel zwischen den Kirchenschiffdachebenen? In welchem
Winkel stehen die Dachflächen zum Grundriss?
  34 
 

d) Ein Sonnenstrahl fällt aus Richtung v   5  ein. Fällt der Schatten der Kreuzspitze
  35 


auf eine der Dachflächen? Bestimme gegebenenfalls die Koordinaten des
Schattenpunkts.
e) Die Kirche wird nachts von Strahlern beleuchtet, die senkrecht zur Ebene ENOP
ausgerichtet sind. Wohin fällt der Schatten der Dachkante, wohin der der Kreuzspitze?
Berechne die Koordinaten für Anfangs- und Endpunkt des Schattens der Dachkante
und des Schattenpunkts der Kreuzspitze.
Seite 2 von 2
12.2 Leistungskurs Mathematik
2. Klausur
Schuljahr 2004/2005
07.06.2005 Munk
Analytische Geometrie – Lagebeziehungen
Name: _____________________________________
Aufgabe 2:
Bei einer Flugübung ist nicht bekannt, zu welchem Zeitpunkt sich welches Flugzeug wo
genau aufhält. Es soll allerdings sichergestellt werden, dass kein Zusammenstoß erfolgen
kann.
a) Wie müssen die „Luftstraßen“ im kritischen Bereich zu einander liegen, dass eine
Kollision auf jeden Fall ausgeschlossen ist?
b) Von Flugzeug A sind die Wegkoordinaten, A ( 2 / 2 / 1) B ( 3 /  2 / 1 ) bekannt, von
Flugzeug B C ( 4 / 0 /  1) D ( 2 / 12 / 2) . Stelle für beide Luftstraßen
Geradengleichungen auf und weise die Bedingung aus a) nach.
c) Berechne den denkbar kleinsten Abstand, den die Maschinen zu einander haben
können.
Aufgabe 3:
Gegeben sind die drei Punkte A (1 / 7 / 4 ), B (  5 / 3 /  4 ), C (  2 /  3 / 0 ) und die
 4  2  t 
  

Geradenschar gt: x   2   k   t 2  mit k , t IR .
 8   3 t 
  

a) Stelle für die Ebene durch die Punkte ABC eine Parameter- und eine Normalenform
auf.
[ mögliche Lösung in Koordinatenform: -8x + 6z=16]
b) Welchen Abstand hat der Punkt P ( 2 / 3 / 5 ) von der Ebene EABC?
c) Bestimme den Parameter t so, dass die Gerade gt komplett in der Ebene E liegt. Wie
liegen die anderen Geraden der Schar zu EABC?
d) Gibt es auch einen Parameter t, für den gt senkrecht zur Ebene EABC ist?
  2
3
 

 
e) Weise nach, dass die Gerade h: x   5   m  1  mit m IR parallel zur Ebene E ist.
 1
4
 
 
f) Welchen Abstand hat h von EABC?
g) Bestimme eine Parameterform der Bildgeraden h’ von h nach Spiegelung an EABC.

Viel Erfolg!