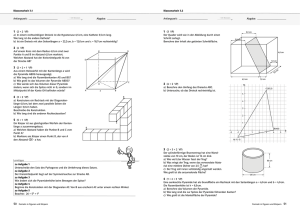
Lk Mathematik in 12/2 2. Klausur 10. 06. 2010 1. Ebenenschar 2

Lk Mathematik in 12/2
1.
2. Klausur
10. 06. 2010
Ebenenschar
Gegeben ist die Ebenenschar
Ek :
k 2 − 2 x1 + 3x2 + 2kx3 − 7 = 0,
k ∈ R.
2 BE
a) Für welche Werte von k beinhalten die Ebenen den Punkt (0 | 0 | 7)?
3 BE
b) Berechne den Schnittpunkt S der Ebene E0 mit der Geraden
 
 
1
1



g : ~x = 2 + λ 1 ,
0
2
λ ∈ R.
3 BE
c) Gib an, für welche Werte von k die Ebenen parallel zur x1 -Achse liegen.
5 BE
d) Bestimme diejenigen Werte von k , für welche die Ebenen vom Ursprung einen
Abstand von 1 haben.
2.
Pyramide
Die vier Punkte A (4 | 0 | 0), B (0 | 9 | 2), C (0 | 0 | 2) und D (2 | 4 | 6) spannen eine
Pyramide P auf.
3 BE
a) Fertige eine saubere Zeichnung der Pyramide in einem
Koordinatensystem der rechts gezeichneten Art.
2 BE
b) Zeige, dass das Dreieck ABD bei D rechtwinklig ist.
3 BE
c) Zeige, dass die Gerade AC senkrecht auf der durch C ,
B und D aufgespannten Ebene ECBD steht.
3 BE
4 BE
d) Berechne den Volumeninhalt V der Pyramide P .
e) Berechne den (spitzen) Winkel ϕ, welchen die Dreiecksächen ABC und ABD
miteinander einschlieÿen, auf eine Dezimale genau.
Hinweis: Betrachte geeignete Normalenvektoren beider Flächen.
5 BE
f) In der Pyramidengrundäche ABC wird die Höhe h zum Punkt D errichtet.
Berechne die Koordinaten des Höhenfuÿpunktes H .
3 BE
g) Bestimme den Umkreismittelpunkt M des rechtwinkligen Dreiecks ADC . Gib
eine kurze Begründung.
4 BE
h) Die Pyramide P besitzt eine Umkugel, auf deren Oberäche alle Eckpunkte
liegen. Bestimme die Koordinaten des Umkugelmittelpunkts U. Begründe die
Vorgehensweise.
40 BE
Viel Erfolg !
Kink
Lk Mathematik in 12/2
2. Klausur
10. 06. 2010
Musterlösung
Ek :
1. Geg.:
k 2 − 2 x1 + 3x2 + 2kx3 − 7 = 0,
2 BE
a) Setze (0 | 0 | 7) ein:
3 BE
b) Setze g in E0 ein:
k 2 − 2 · 0 + 3 · 0 + 2k · 7 − 7 = 0
14k = 7
1
k=
2
 
 
1
1



g : ~x = 2 + λ 1
0
2
E0 : − 2x1 + 3x2 − 7 = 0
−2 (1 + λ) + 3 (2 + λ) − 7 = 0
λ−3=0
λ=3
 
   
1
1
4
~s = 2 + 3 1 = 5
0
2
6
3 BE
c) Fordere:
k ∈ R.
⇒
S (4 | 5 | 6)
k2 − 2 = 0
√
k=± 2
n √ √ o
Für k ∈ − 2 ; 2
liegen die Ebenen parallel zur x1 -Achse.
5 BE
d) HNF:
1
q
(k 2 − 2)2 + 32 + (2k)2
k 2 − 2 x1 + 3x2 + 2kx3 − 7 = 0
7
7
7
=√
=√
d (O; Ek ) = q
4
2
2
4
k − 4k + 4 + 9 + 4k
k + 13
(k 2 − 2)2 + 32 + (2k)2
Fordere:
7
√
=1
k 4 + 13
√
k 4 + 13 = 7
k 4 + 13 = 49
k 4 = 36
√
k1/2 = ± 6
⇒
n √ √ o
k ∈ − 6; 6
Lk Mathematik in 12/2
2. Klausur
10. 06. 2010
Musterlösung
2. A (4 | 0 | 0), B (0 | 9 | 2), C (0 | 0 | 2), D (2 | 4 | 6)
3 BE
a)
2 BE
b) Skalarprodukte der Richtungsvektoren:

  
−2
2
−−→ −−→    
4 ◦ −5 = 0
AD ◦ BD =
6
4
3 BE
−−→ −−→
AD ⊥ BD
c) Skalarprodukte der Richtungsvektoren:

  
−4
0
−→ −−→    
0 ◦ 9 =0 ⇒
AC ◦ CB =
 2  0
−4
2
−→ −−→    
0 ◦ 4 =0 ⇒
AC ◦ CD =
2
4
3 BE
⇒


−→ −−→ 

AC ⊥ CB 



−→ −−→
AC ⊥ CD
⇒
AC ⊥ ECBD







d) Volumen über das Spatprodukt:
−4 −4 −2 1
−→ −→ −−→ 1
1
0
4 = |180| = 30
V = det AB ; AC ; AD = 9
6
6
6
2
2
6
4 BE
e) Normalenvektoren zu den Dreiecksächen:

~nABC
~noABC
    
 
4
0
18
1
−→ −−→      

0 × 9 = 0 = 18 · 0
= CA × CB =
−2
0
36
2
 
 
1
1
1
1  


√
√
0 =
0
=
12 + 02 + 22 2
5 2
Lk Mathematik in 12/2
2. Klausur
10. 06. 2010
Musterlösung
~nABD
~noABD
    

 
−2
−4
−46
23
−−→ −→
= AD × AB =  4  ×  9  = −20 = −2 10
6
2
−2
1
 
 
23
23
1
10 = √ 1 10
=√
232 + 102 + 12 1
630 1
Die Normalenvektoren schlieÿen denselben Winkel ein wie die Ebenen:
cos ϕ = |~noABC
 
 
1
23 1
25
1
o
≈ 0, 445 44
10 = √
◦ ~nABD | = √ 0 ◦ √
630 1 3150 5 2
ϕ ≈ arccos 0, 445 44 ≈ 63, 5◦
5 BE
f) HNF der Ebene EABC : ~noABC ◦ (~x − ~a) = 0
     
1
x
4
1    1   
√
0 ◦
x2 − 0
=0
5 2
x3
0
1
√ (x1 + 2x3 − 4) = 0
EABC :
5
√
1
d (D; EABC ) = √ (2 + 2 · 6 − 4) = 2 5
5
Abstand:
Der Normalenvektor zeigt in die positive Halbebene, in welcher auch D liegt.
Deshalb gilt für den Höhenfuÿpunkt:
 
 
2
1
√
~h = d~ + 2 5 · ~no = 4 − 2 5 · √1 0
5 2
6
 
   
2
1
0
= 4 − 2 0 = 4 ⇒ H (0 | 4 | 2)
6
2
2
√
3 BE
g) Beim rechtwinkligen Dreieck ist der Umkreis zugleich Thaleskreis. Daher liegt
M genau in der Mitte zwischen A und D:
 
   
4
−2
3
1
1 −−→
m
~ = ~a + AD = 0 +  4  = 2
2
2
0
6
3
4 BE
M (3 | 2 | 3)
h) U muss von allen Eckpunkten gleich weit entfernt sein. Er ist daher zugleich
Umkreismittelpunkt der Dreiecke ABC und ABD. Da beide Dreicke rechtwinklig
sind, ist K der Mittelpunkt der gemeinsamen Hypotenuse [AB]:
 
   
4
−4
2
1 −→   1    
9
~u = ~a + AB = 0 +
= 4, 5
2
2
0
1
2
40 BE
⇒
⇒
M (2 | 4, 5 | 1)