Grundbegriffe der Wahrscheinlichkeitstheorie. Kursfolien

Grundbegriffe der Wahrscheinlichkeitstheorie
Karin Haenelt
11.1.2013
1
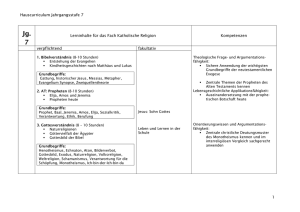
Inhalt
Wahrscheinlichkeitsraum
Bedingte Wahrscheinlichkeit
Abhängige und unabhängige Ereignisse
Stochastischer Prozess
Markow-Kette
© Karin Haenelt, Grundbegriffe der
Wahrscheinlichkeitstheorie,
11.1.2013
2
Wahrscheinlichkeitsraum
Modell zur Beschreibung von Zufallsexperimenten
Ein Wahrscheinlichkeitsraum ist ein normierter Maßraum
Es gilt: Ein Wahrscheinlichkeitsraum ist ein Maßraum (Ω, , P)
Dabei ist
Ω eine Menge
eine σ-Algebra in Ω, und
P ein Maß auf mit der Normierungsbedingung P(Ω) = 1.
Bauer, 2001, 4
© Karin Haenelt, Grundbegriffe der
Wahrscheinlichkeitstheorie,
11.1.2013
3
σ-Algebra
eine Mengenalgebra, die unter abzählbar unendlichen
Vereinigungen abgeschlossen ist
Mengensystem über Ω mit folgenden Eigenschaften
ø∊
A∊ ⇒ A ∊
A1, A2, … ∊ ⇒ ∪i Ai ∊
Die Elemente A der σ-Algebra eines
Wahrscheinlichkeitsraumes (Ω, , P) heißen Ereignisse
Die Elemente ω von Ω heißen Elementarereignisse
© Karin Haenelt, Grundbegriffe der
Wahrscheinlichkeitstheorie,
11.1.2013
4
Wahrscheinlichkeitsmaß
P(A) ist die Wahrscheinlichkeit von A oder für das Eintreten des
Ereignisses A.
eine Abbildung P : A → [1,0] mit den Eigenschaften
P(A) ≥ 0 für jedes A ∊
Gilt
A1, A2, … ∊ mit Ai ∩ Aj = ∅ für i ≠ j,
∞
∞
so gilt P (∪ Ai ) = ∑ P ( Ai )
i =1
i =1
P(Ω) = 1
© Karin Haenelt, Grundbegriffe der
Wahrscheinlichkeitstheorie,
11.1.2013
5
Komponenten des Wahrscheinlichkeitsraumes
Bezeichnung
Erläuterung
(Ω, ,P)
Wahrscheinlichkeits
raum
Ω
Ergebnismenge
Menge aller Elementarereignisse
ω
Elementarereignis
Element von Ω
σ-Algebra über Ω
Ereignisraum
Menge aller möglichen
Ereignisse;
-Nicht notwendigerweise
jede Teilmenge von Ω,
mindestens
- Ω als sicheres Ereignis
- ∅ als unmögliches
Ereignis
A ∈ σ-Algebra
über Ω
Ereignis
© Karin Haenelt, Grundbegriffe der
Wahrscheinlichkeitstheorie,
11.1.2013
6
Komponenten des Wahrscheinlichkeitsraumes:
Beispiel 1
Bezeichnung
Beispiel
(Ω, ,P)
Wahrscheinlichkeits
raum
Ω
Ergebnismenge
{a,b,c}
ω
Elementarereignis
a
σ-Algebra über Ω
Ereignisraum
{ {a,b,c}, {a,b},{a,c}, {a}, {b,c},
{b}, {c}, {} }
A ∈ σ-Algebra
über Ω
Ereignis
{a,b,c}
© Karin Haenelt, Grundbegriffe der
Wahrscheinlichkeitstheorie,
11.1.2013
7
Komponenten des Wahrscheinlichkeitsraumes:
Beispiel 2 (Verkehrsampel)
Bezeichnung
Beispiel
(Ω,F,P)
Wahrscheinlichkeits
raum
Ω
Ergebnismenge
{rot,gelb,grün}
ω
Elementarereignis
gelb
σ-Algebra über Ω
Ereignisraum
{ {rot}, {rot,gelb},{gelb}, {grün}, {}
}
A ∈ σ-Algebra
über Ω
Ereignis
{rot,gelb}
© Karin Haenelt, Grundbegriffe der
Wahrscheinlichkeitstheorie,
11.1.2013
8
Inhalt
Wahrscheinlichkeitsraum
Bedingte Wahrscheinlichkeit
Abhängige und unabhängige Ereignisse
Stochastischer Prozess
Markow-Kette
© Karin Haenelt, Grundbegriffe der
Wahrscheinlichkeitstheorie,
11.1.2013
9
Bedingte Wahrscheinlichkeit
P(A)
Wahrscheinlichkeit (a priori Wahrscheinlichkeit)
Gesamtmenge
A
P(A|B)
A∩B B
- betrachtet eine Teilmenge aus der Gesamtmenge
- P(A) / P(Gesamtmenge) = P(A) / 1 = P(A)
Bedingte Wahrscheinlichkeit (a posteriori Wahrscheinlichkeit)
Gesamtmenge
A
- Wahrscheinlichkeit, dass Ereignis A eintritt
A∩B B
© Karin Haenelt, Grundbegriffe der
Wahrscheinlichkeitstheorie,
11.1.2013
- Wahrscheinlichkeit
- dass Ereignis A eintritt,
- wenn Ereignis B eingetreten ist
- betrachtet eine Teilmenge aus einer Teilmenge
- P(A|B) = P(A B) / P(B)
10
Das Pferd „Harry“ und das Wetter
Rennen
Gesamt bei Regen
gewonnen
verloren
gelaufen
20
80
15
15
100
30
5
65
15
15
Einfache Wahrscheinlichkeit P(A)
betrachtet Teilmengen aus der Gesamtmenge, Beispiele
P( win) = .2
P ( win) / P( gesamt)
P( win ∩ rain) = .15
P( win ∩ rain) / P( gesamt)
Bedingte Wahrscheinlichkeit P(A|B)
betrachtet Teilmengen aus einer Teilmenge, Beispiel
P( win | rain) = .5
P ( win ∩ rain) / P(rain)
© Karin Haenelt, Grundbegriffe der
Wahrscheinlichkeitstheorie,
11.1.2013
11
Bedingte Wahrscheinlichkeit
Definition
P(A | B) =
P(A ∩ B)
P(B)
P(Win | Rain) =
P(Win ∩ Rain)
P(Rain)
Schreibvarianten
P(A | B) =
P(A, B)
P(B)
P(Win | Rain) =
.15
= .5
.30
P(A | B) = P(A & B) / P(B)
P(A|B) ≠ P(B|A)
A A∩B
5
65
© Karin Haenelt, Grundbegriffe der
Wahrscheinlichkeitstheorie,
11.1.2013
15
B
P(Rain | Win) =
P(Rain ∩ Win)
P(Win)
P(Rain | Win) =
.15
= .75
.20
15
12
P(A | B) =
P(A ∩ B)
P(B)
Theorem von Bayes
ermöglicht Berechnung von P(B|A) aus P(A|B)
Regel von Bayes
P(A ∩ B)
= P(B) · P(A ∩ B) / P(B) = P(B) · P(A|B)
0.3 ·
.15
/
0.3 = 0.3 ·
= P(A) · P(A ∩B) / P(A)
0.2 ·
.15
/
0.5
= 0.15
= P(A) ·P(B|A)
0.2 = 0.2 ·
0.75
= 0.15
Theorem von Bayes
P(A|B )= P(A ∩ B) / P(B)
= P(B) · P(A|B) / P(B)
0.3 ·
Herleitung durch Umformung
0.5 / 0.3 = 0.50
= P(A) ·P(B|A) / P(B)
0.2 · 0.75 / 0.3 = 0.50
© Karin Haenelt, Grundbegriffe der
Wahrscheinlichkeitstheorie,
11.1.2013
13
5
A:win
A∩B
15
B:rain
65
Theorem von Bayes
15
ermöglicht Berechnung von P(B|A) aus P(A|B
Regel von Bayes
P(A ∩ B)
= P(B) · P(A ∩ B) / P(B) = P(B) · P(A|B)
0.3 ·
.15
/
0.3 = 0.3 ·
= P(A) · P(A ∩B) / P(A)
0.2 ·
.15
/
0.5
= 0.15
= P(A) ·P(B|A)
0.2 = 0.2 ·
0.75
= 0.15
Theorem von Bayes
P(A|B )= P(A ∩ B) / P(B)
= P(B) · P(A|B) / P(B)
0.3 ·
0.5 / 0.3 = 0.50
= P(A) ·P(B|A) / P(B)
Herleitung durch Umformung 0.2 · 0.75 / 0.3 = 0.50
© Karin Haenelt, Grundbegriffe der
Wahrscheinlichkeitstheorie,
,
11.1.2013
14
Inhalt
Wahrscheinlichkeitsraum
Bedingte Wahrscheinlichkeit
Abhängige und unabhängige Ereignisse
Stochastischer Prozess
Markow-Kette
© Karin Haenelt, Grundbegriffe der
Wahrscheinlichkeitstheorie,
11.1.2013
15
Unabhängige Ereignisse
Zwei Ereignisse sind voneinander unabhängig, wenn gilt:
P(A|B)
= P(A)
P(A ∩ B)
= P(A) · P(B)
Typisches Beispiel:
Es werden zwei Würfel geworfen.
Sei A das Ereignis: der 1. Wurf ist eine 1: P(A) = 1/6
Sei B das Ereignis: der 2. Wurf ist eine 6: P(B) = 1/6
Wahrscheinlichkeit A und B: P(A∩B) = 1/6 · 1/6 = 1/36
© Karin Haenelt, Grundbegriffe der
Wahrscheinlichkeitstheorie,
11.1.2013
16
Test zweier Ereignisse
auf Unabhängigkeit
Rennen
P(win|rain)
5
65
40
40
gewonnen
20
15
10
verloren
80
15
40
Gesamt
100
30
50
P(win)
Ergebnis:
die Ereignisse „win“ und „rain“ sind
≠ .20
abhängig
Beispiel 2 .20
= .20
unabhängig
P(win) · P(rain) Ergebnis:
die Ereignisse „win“ und „rain“ sind
Beispiel 1 .15
≠ .2 × .3 = .06
abhängig
Beispiel 2 .10
= .2 × .5 = .10
unabhängig
© Karin Haenelt, Grundbegriffe der
Wahrscheinlichkeitstheorie,
11.1.2013
15
alle Rennen bei Regen bei Regen
(Beispiel 1) (Beispiel 2)
Beispiel 1 .50
P(win ∩ rain)
10 10
15
17
17
Abhängige und unabhängige Ereignisse
diese Formeln gelten in beiden Fällen, da die rechte und die
linke Seite äquivalent sind
P(A ∩ B)
= P(A) ·P(B | A) = P(B) · P(A | B)
P(A | B)
= P(A ∩ B) / P(B)
P(win ∩ rain) = P(win|rain)
·
P(rain)
= P(rain|win)
· P(win)
Beispiel 1
.15
·
.3
= .75
· .2
Beispiel 2
.10
P(win|rain)
Beispiel 1
.5
.15
/ .3
Beispiel 2
.2
.10
/.5
© Karin Haenelt, Grundbegriffe der
Wahrscheinlichkeitstheorie,
11.1.2013
= .5
= .2
·
= P(win ∩rain)
.5
= .5
/ P(rain)
· .2
18
Inhalt
Wahrscheinlichkeitsraum
Bedingte Wahrscheinlichkeit
Abhängige und unabhängige Ereignisse
Stochastischer Prozess
Markow-Kette
© Karin Haenelt, Grundbegriffe der
Wahrscheinlichkeitstheorie,
11.1.2013
19
Stochastischer Prozess
Definition 1
Sei Ω eine Menge elementarer Zufallsereignisse
(Ergebnismenge eines Wahrscheinlichkeitsraumes).
Ein stochastischer Prozess oder Zufallsprozess ist eine
Folge von elementaren Zufallsereignissen
X1,X2,…Xi ∈ Ω
Definition 2
Die möglichen Zufallswerte in einem stochastischen Prozess
heißen Zustände des Prozesses.
Man sagt, dass sich der Prozess zum Zeitpunkt t in Zustand
Xt befindet
Brants, 1999: 30
© Karin Haenelt, Grundbegriffe der
Wahrscheinlichkeitstheorie,
11.1.2013
20
Stochastischer Prozess
Für die vollständige Beschreibung eines Zufallsprozesses mit
diskretem Zeitparameter benötigt man
1. die Anfangswahrscheinlichkeit:
die für jeden Zustand angibt, mit welcher
Wahrscheinlichkeit er als Zustand X1 beobachtet werden
kann (d.h. den Startzustand bildet)
πi = P(X1=si)
2. die Übergangswahrscheinlichkeit:
die für jeden Zustand angibt, mit welcher
Wahrscheinlichkeit er in einer Zustandsfolge auftritt:
P(Xt+1 = xt+1 | X1 = x1, X2 = x2, …,Xt = xt)
Brants, 1999: 30
© Karin Haenelt, Grundbegriffe der
Wahrscheinlichkeitstheorie,
11.1.2013
21
Stochastischer Prozess: Beispiel
Ein Textgenerator hat ein Lexikon mit drei Wörtern von denen
an jeder Position jedes auftreten kann :
Ω = {geschickt, werden, wir}
wir beobachten an jeder Position, welches Wort generiert wurde
Sei
X1 das Wort zum ersten Beobachtungszeitpunkt
X2 das Wort zum zweiten Beobachtungszeitpunkt, usw.
Dann ist die Folge der Wörter ein stochastischer Prozess mit
diskreter Zufallsvariable und diskretem Zeitparameter
Für diese Folge kann man eine Wahrscheinlichkeit angeben
© Karin Haenelt, Grundbegriffe der
Wahrscheinlichkeitstheorie,
11.1.2013
22
Inhalt
Wahrscheinlichkeitsraum
Bedingte Wahrscheinlichkeit
Abhängige und unabhängige Ereignisse
Stochastischer Prozess
Markow-Kette
© Karin Haenelt, Grundbegriffe der
Wahrscheinlichkeitstheorie,
11.1.2013
23
Markow-Kette
Eine Markow-Kette ist ein stochastischer Prozess, bei dem der
nächste Zustand Xt+1 bei bekanntem gegenwärtigem Zustand Xt
unabhängig von den vergangenen Zuständen Xt-1, Xt-2,…,X0 ist.
Es gilt
P(Xt+1 = j | Xt = it, Xt-1 = it-1, …,X1 = i1, X0=i0) =
P(Xt+1 = j | Xt = it)
daher der Name Kette: Kettenglieder hängen nur am vorigen
Kettenglied, nicht an allen vorherigen Kettengliedern
Brants,Crocker,Lieblang, 2000:22
© Karin Haenelt, Grundbegriffe der
Wahrscheinlichkeitstheorie,
11.1.2013
24
Endliche Markow-Kette
Für eine endliche Markow-Kette gibt es endlich viele Zustände,
und die Kette muss sich zu jedem Zeitpunkt in einem dieser
endlich vielen Zustände befinden
Brants, 1999: 31
Prozess
„ohne Gedächtnis“
mit endlich vielen Zuständen
entspricht den Eigenschaften eines endlichen Automaten
© Karin Haenelt, Grundbegriffe der
Wahrscheinlichkeitstheorie,
11.1.2013
25
Markow-Kette und Eigenschaften menschlicher
Sprachen: ein Beispiel
nach einem q folgt oft ein u,
Vorhersage über 2. Buchstaben hinter q?
abhängig von q?
nach einem s folgt ein c, dann folgt ein h
Vorhersage über 3. Buchstaben hinter s?
abhängig von s?
Markow-Modell
1. Ordnung
Markow-Modell
2. Ordnung
…
Kunze, 2001
© Karin Haenelt, Grundbegriffe der
Wahrscheinlichkeitstheorie,
11.1.2013
26
Markow-Kette: Matrix-Darstellung
kann beschrieben werden durch die Angaben
Stochastische Übergangsmatrix A
aij = P ( Xt + 1 = sj | Xt = si )
∀i, j
aij ≥ 0
N
∀i
∑a
i, j
j =1
=1
Anfangswahrscheinlichkeiten Π
πi = P( X 1 = si )
N
∑π
i
=1
i =1
Xt = si
Xt + 1 = sj
geschickt
geschickt .3
werden .4
wir
.3
Xt
werden
.4
.2
.4
π
geschickt .2
werden .3
wir
.5
Manning/Schütze, 2000: 318
© Karin Haenelt, Grundbegriffe der
Wahrscheinlichkeitstheorie,
11.1.2013
27
wir
.3
.4
.3
Markow Model: Definition
Ein Markow-Modell wird spezifiziert durch ein Tripel (S,Π,A)
S = {S1, ..., SN} Menge der Zustände
Π = {πi}
Wahrscheinlichkeiten der Startzustände
πi = P(X1 = Si)
N
∑π = 1
i
i =1
A = {aij}
Wahrscheinlichkeiten der Zustandsübergänge
N
aij = P(Xt+1 = Sj | Xt = Si)
1≤i,
∑ aij = 1
j≤N
j =1
© Karin Haenelt, Grundbegriffe der
Wahrscheinlichkeitstheorie,
11.1.2013
28
Markow-Kette: Graph-Darstellung
kann beschrieben werden durch Zustandsübergangsgraphen
.5
.3
.3
.4
.2
wir
.4
werden
.3
.4
.3
.4
geschickt
.2
© Karin Haenelt, Grundbegriffe der
Wahrscheinlichkeitstheorie,
11.1.2013
.3
29
Markow-Kette: Berechnung einer SequenzWahrscheinlichkeit
Wahrscheinlichkeit der Sequenz der Zustände X1 … XT
P ( X 1,..., XT )
= P( X 1) P( X 2 | X 1) P( X 3 | X 2, X 1)...P( XT | X 1,..., XT − 1)
für eine Markow-Kette gilt:
= P ( X 1) P ( X 2 | X 1) P ( X 3 | X 2)...P ( XT | XT − 1)
=π
T −1
X1Π
t =1
a X t X t +1
Manning/Schütze, 2000: 320
© Karin Haenelt, Grundbegriffe der
Wahrscheinlichkeitstheorie,
11.1.2013
30
Markow-Kette: Berechnungsbeispiel
Wahrscheinlichkeit der Sequenz der Zustände X1 … XT
P( X 1 = wir , X 2 = werden, X 3 = geschickt )
= P ( X 1 = wir ) ⋅
P ( X 2 = werden | X 1 = wir ) ⋅
P ( X 3 = geschickt | X 2 = werden)
= (.5 × .4 × .4) = 0.08
© Karin Haenelt, Grundbegriffe der
Wahrscheinlichkeitstheorie,
11.1.2013
Xt
π
geschickt .2
werden .3
wir
.5
Xt = si
Xt + 1 = sj
geschickt
geschickt .3
werden .4
wir
.3
werden
.4
.2
.4
wir
.3
.4
.3
31
Literatur
•
•
•
•
•
Bauer, Heinz (2001). Wahrscheinlichkeitstheorie. de Gruyter. 5. verbesserte Auflage.
Brants, Thorsten (1999). Statistische Methoden in der Sprachverarbeitung. Seminarskript
15. Juni 1999
Brants, Thorsten; Matthew Crocker und Enrico Lieblang (2000). Statistische Methoden in
der Sprachverarbeitung. Seminarskript. http://www.coli.unisaarland.de/~thorsten/stat00/skript.ps.gz
Manning, Christopher D.; Schütze, Hinrich (1999): Foundations of Statistical Natural
Language Processing. Cambridge, Mass., London: The MIT Press. (vgl.:
http://www.sultry.arts.usyd.edu.au/fsnlp)
Versionen 11.1.2013, 26.5.2009
© Karin Haenelt, Grundbegriffe der
Wahrscheinlichkeitstheorie,
11.1.2013
32