Übungen zur Vorlesung Statistische Methoden

TECHNISCHE UNIVERSITÄT DORTMUND
FAKULTÄT STATISTIK
Dr. M. Arnold
Dipl.-Stat. M. Bücker
Sommersemester 2009
Übungsblatt 6
18.05.2009
Übungen zur Vorlesung Statistische Methoden
Aufgabe 23:
Sei X ∼ Re(θ1 , θ2 ) eine auf dem Intervall [θ1 , θ2 ] rechteckverteilte Zufallsvariable, mit
θ1 , θ2 ∈ R und θ1 < θ2 . Die Dichte von X ist gegeben durch
(
1
θ1 ≤ x ≤ θ2
f (x; θ1 , θ2 ) = θ2 −θ1
.
0
sonst
Bestimmen Sie die Momentenschätzer für θ1 und θ2 .
Aufgabe 24:
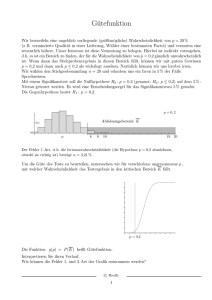
Für die Schokoladentafeln des Schokoladenherstellers Schoko ist bekannt, dass ihr Gewicht X eine normalverteilte Zufallsgröße ist mit X ∼ N(µ, σ 2 ), wobei σ 2 = 1.44 gilt.
Nach Angaben der Firma Schoko wiegen die Tafeln im Mittel 100 Gramm. Ein Abnehmer, der die Tafeln weitervertreibt, hat jedoch Zweifel an der Behauptung des Herstellers.
Es ist also das folgende Testproblem zu untersuchen
H0 : µ = 100 gegen H1 : µ 6= 100.
Zur Entscheidung für eine der Hypothesen anhand einer Stichprobe X1 , . . . X10 aus 10
Tafeln soll als Prüfgröße das durchschnittliche Gewicht X̄ betrachtet werden. Ist das
durchschnittliche Gewicht deutlich größer oder deutlich kleiner als 100, so spricht dies
gegen H0 (also gegen die Behauptung des Herstellers). Ist X̄ hingegen etwa 100, so ist
dies ein Hinweis für H0 .
(a) Es werden nun zwei Tests vorgeschlagen: Test A lehnt die Nullhypothese ab, falls
X̄ > 100.5 oder X̄ < 99.5 ist. Test B lehnt die Nullhypothese ab, falls X̄ > 101
oder X̄ < 99 gilt. Bestimmen Sie die Wahrscheinlichkeit für einen Fehler 1. Art für
diese Tests.
Hinweis: Nutzen Sie dazu aus, dass unter Annahme der Nullhypothese gilt
√ X̄ − 100
n
∼ N(0, 1).
σ
(b) Bestimmen Sie nun die Wahrscheinlichkeit für einen Fehler 2. Art in Abhängigkeit
des wahren Parameters µ = 98 für beide Tests.
Aufgabe 25:
Eine Umfrage unter 30 Studierenden einer Universität im vergangenen Jahr ergab, dass
50% der Befragten regelmäßig mindestens zweimal wöchentlich für 30 Minuten Sport
treiben. Es wird vermutet, dass der Anteil p der Sporttreibenden mittlerweile kleiner
als 50% ist. Zur Untersuchung dieser Vermutung wird eine erneute Umfrage unter 30
Studierenden durchgeführt. Getestet werden sollen nun die Hypothesen
H0 : p = 0.5 gegen H1 : p < 0.5.
Es werden zwei Tests vorgeschlagen, die beide als Teststatistik X, die Anzahl der Sportreibenden unter den Befragten, verwenden. Test A lehnt die Nullhypothese ab, falls
weniger als 10 Studenten regelmäßig Sport treiben, Test B lehnt H0 ab, falls weniger als
12 Studenten regelmäßig Sport treiben.
(a) Bestimmen Sie für Test A und B jeweils die Wahrscheinlichkeit für einen Fehler 1.
Art. Welchen Test würden Sie bezüglich des Fehlers 1. Art bevorzugen?
(b) Bestimmen Sie nun die Wahrscheinlichkeit für einen Fehler 2. Art in Abhängigkeit
des wahren Parameters p ∈ {0.1, 0.2, 0.3, 0.4} und zeichnen Sie diese für beide Tests.
(c) Bestimmen Sie nun den kritischen Wert der Teststatistik X für den Test mit Signifikanzniveau α = 0.05.