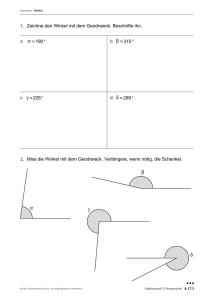
Eulersche Winkel, Drehmatrizen und Spin.nb

Eulersche Winkel, Drehmatrizen und Spin.nb
1
Eulersche Winkel, Drehmatrizen und Spin
Vortrag im Seminar zur Theoretischen Physik von Torsten Pfoh und Johannes Bernhard
Wiederholung:
Im letzten Vortrag über Erzeugende von Drehungen und ihre Darstellungen sind wir analog zur Mechanik von einer
kartesischen Basis ausgegangen und erhielten für die Erzeugenden die Matrizen
ij 0 0 0 yz
j
z
J1 = jjjj 0 0 -1 zzzz
j
z
k0 1 0 {
ij 0 0 1 yz
j
z
J2 = jjjj 0 0 0 zzzz
j
z
k -1 0 0 {
ij 0 -1 0 yz
j
z
J3 = jjjj 1 0 0 zzzz
j
z
k0 0 0 {
Die Jk sind jedoch antisymmetrisch bzw. als Matrizen über anthihermitesch. Um die unitären Transformationen D(R)
(R Œ SO(3)) als Exponentialfunktion in den Erzeugenden und Drehwinkeln darstellen zu können, wurde zunächst
folgende Definition vorgenommen:
é
è è
wobei @J1 , J2 D = i J3 HzyklischL
è
Jk := i Jk
Die so definierten Erzeugenden sind nun hermitesch, ihr Kommutator ist antihermitesch. Nun wäre es von Vorteil,
zumindest eine der Erzeugenden in diagonale Form zu bringen. Hierzu wechselt man von kartesischen Koordinaten mit
Ô Ô Ô
den Einheitsvektoren (e1 ,e2 ,e3 ) auf die sogenannten sphärischen Koordinaten mit sphärischen Einheitsvektoren:
Ô
Ô
1
z1 := - ÅÅÅÅ
ÅÅÅÅ!ÅÅ (e1 +i e2 ),
è!!!!
2
Ô
z0 := e3 ,
zm* = H-Lm z-m
dabei gelten
Ô
Ô
1
z-1 := + ÅÅÅÅ
ÅÅÅÅ!ÅÅ (e1 -i e2 )
è!!!!
2
und
zm* . zm£ = dmm£
è
Die Matrixdarstellungen der Jk in der neuen Basis ergeben dann gerade die Matrizen fürden Bahndrehimpuls mit l =1
und werden im folgenden schlicht als Jk bezeichnet:
è!!!!
2 0 zy
jij 0
z
j è!!!!
! zzzz
1 j
j
J1 = ÅÅÅÅ2 jj 2 0 è!!!
2
zz
jj
zz
j
è!!!!
2
0
0
k
{
è!!!!
0
jij 0 - 2
j è!!!!
è!!!
!
i j
j
J2 = ÅÅÅÅ2 jj 2
0
- 2
jj
j
è!!!!
2
0
k 0
zyz
zz
zz
zz
zz
{
1 0 0 y
jij
zz
j
J3 = jjj 0 0 0 zzzz
j
z
k 0 0 -1 {
In dieser Darstellung ist die 1-Komponente reell und positiv, die 2-Komponente rein imaginär und die 3-Komponente
schließlich diagonal. Der Kommutator ist natürlich invariant unter Basiswechsel, daher gilt allg.
@Jm , Jk D = i
(1)
3
l=1 emkl Jl
Führt man nun analog zum Bahndrehimpuls das Quadrat J2 = J1 2 +J2 2 +J3 2 und die Leiteroperatoren J = J1 ± iJ2 ein,
so erhält man folgende wichtige Relationen
@J3 , J D = ±J±
@J+ , J- D = 2J3
J2 = J± J° + J3 2 ¡J3
(2)
Eulersche Winkel, Drehmatrizen und Spin.nb
2
Ist nun » bm \ ein gemeinsamer Eigenzustand von J2 und J3 mit den jeweiligen Eigenwerten b und m, dann ist auch
J± » bm \ Eigenzustand und es gilt
J » bm \ = c » b, m±1 \
(3)
Bildet man jetzt das Normquadrat J » bm \¥2 , so erhält man mit Hilfe der Formeln aus (2) für das Betragsquadrat
des Koeffizienten c gerade
c ¥2 = b - m(m±1), also c = ei j
è!!!!!!!!!!!!!!!!!!!!!!!!!!!!
b - mHm 1L
(4)
Aus (4) folgen die Ungleichungen b - m(m+1) ¥ 0 und b - m(m-1) ¥ 0
Aus der ersten ersten erhalten wir mit j:= mmax b = j(j+1), die zweite Ungleichung liefert mmin = –j .
Damit die Reihe der m-Werte beginnend bei mmin = -j auch tatsächlich auf mmax = jtrifft und dort abbricht, muss j ¥ 0
und ganz-oder halbzahlig sein. Als Ergebnis erhält man die Eigenwertspektren
J2 » jm \ = j(j+1) » jm \
und
J3 » jm \ = m » jm \
j = 0, ÅÅ12ÅÅ , 1, ÅÅÅÅ32 , 2, ...
m = -j, -j+1,..., j-1, j
(5)
Phasenkonvention
Im folgenden wählen wir die Phase so, dass die Matrixelemente der Auf-und Absteigeoperatoren in der Basis der
Eigenfunktionen reell werden, d.h.
Xj´m´»J± »jm\ =
(6)
è!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
j Hj + 1L - mHm 1L d j´, j dm´, m
1
Dieses erreicht man schlicht durch die Wahl j = 0. Diese Konvention ist in der Theorie der Drehgruppe allgemein
üblich und wird als Condon-Shortley-Phasenkonvention bezeichnet.
Kehren wir zu den kartesischen Komponenten zurück indem wir J1 und J2 durch die Leiteroperatoren ausdrücken
J1 = (J+ - J- )/2
J2 = -i (J+ - J- )/2 ,
so erhalten wir mit obiger Phasenkonvention und unter Verwendung der Gl. (6) zu festem j die Matrixelemente der Jk
è!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
X m£ » J1 » m \ = ÅÅÅÅ12 j Hj + 1L - m£ m (dm£ ,m+1 + dm£ ,m-1 )
X m£ » J2 » m \ = X m£ » -i [J3 ,J1 ]» m \ = -i (m£ - m) X m£ » J1 » m \
X m£ » J3 » m \ = m dm£ ,m
(7)
Die ausführlichen Rechenschritte finden sich im Vortrag zu Erzeugenden und ihren Darstellungen von Andreas Müller.
Eulersche Winkel, Drehmatrizen und Spin.nb
3
Konstruktion der "Drehmatrizen" DH jL
Die Matrizen D(R) werden inhaltlich korrekt als Darstellungskoeffizienten der Drehgruppe bezeichnet, im
Sprachgebrauch verwendet man jedoch "Drehmatrizen" oder schlicht "D-Matrizen". Wie anfangs erwähnt, bezeichnen
die D(R) unitäre Transformationen im abzählbar unendl. dimensionalen Hilbertraum. Um die D-Matrizen zu
konstruieren, benötigt man zunächst eine geeignete Parametrisierung. Im 3 lässt sich eine Drehung durch Eulersche
Winkel parametrisieren. In der Quantenmechanik ist hierbei jedoch eine andere Definition als in der klassischen
Mechanik üblich.
Diese unterscheidet sich durch die Wahl der sogenannten Knotenlinie h. Wir beginnen mit einer Drehung um die alte
3-Achse um den Winkel f, es folgt eine Drehung um die Zwischenposition der 2-Achse (Knotenlinie) um den Winkel q,
zuletzt drehen wir um die neue 3-Achse um den den Winkel y. (in F.Scheck, Mechanik, s.188 sind diese Winkel mit
a, b, g bezeichnet). Es gelten folgende Definitionsnbereiche: 0 § f § 2 p , 0 § q § p , 0 § y § 2 p
Wählen wir nun eine Basis, in der J2 diagonal ist, so zerfällt D(R) nach dem 2. Schurschen Lemma in quadratische
Blöcke entlang der Hauptdiagonalen. Jeder dieser Blöcke gehört zu einem Wert für j und hat aufgrund der Richtungsquantelung die Dimension d = (2j+1). Die Werte von j werden hierbei aufsteigend angeordnet, die Werte von m zu
festen j in den Unterräumen H jL in absteigender Reihenfolge. Man erhält
i
DH0L
0
0
0
0
0
0,0
j
j
j
j
j
DH1ê2L
DH1ê2L
0
0
0
j 0
1ê2,1ê2
1ê2, 1ê2
j
j
j
j
H1ê2L
H1ê2L
j
j
0
D 1ê2,1ê2 D 1ê2, 1ê2
0
0
0
j
j
j
j
H1L
H1L
H1L
j
j
0
0
0
D1,1 D1,0 D1, 1
j
j
j
j
j
j
0
0
0
DH1L
DH1L
DH1L
j
0,1
0,0
0, 1
j
j
j
H1L
H1L
H1L
j
j 0
0
0
D 1,1 D 1,0 D 1, 1
j
j
j
:
:
:
:
:
:
k
H8L
Innerhalb jedes Unterraumes
gegeben durch
H jL
.. y
z
z
z
z
.. z
z
z
z
z
z
z
.. z
z
z
z
z
z
.. z
z
z
z
z
z
.. z
z
z
z
z
z
.. z
z
z
z
{
zu festem j ist, unter Verwendung der Eulerschen Winkel, die D-Matrix somit
Eulersche Winkel, Drehmatrizen und Spin.nb
4
DH jL = exp(i y J3 ) exp(i q J2 ) exp(i f J3 )
Jetzt macht es sich bezahlt, dass wir J3 mittels Darstellung in sphärischen Koordinaten diagonalisiert haben.
Für die Matrixelemente von DH jL gilt jetzt nämlich
H jL
£
Dm£ m (y, q, f) = ei m
y
H jL
£
dm£ m (q) ei m
f
wobei
dm£ m (q) = Xj£ m£ » exp Hi q J2 L » jm \
H jL
(9)
Die Berechnung der D-Matrix reduziert sich somit auf die Berechnung von d(q).
Phasenkonvention für D-Matrizen
Während die Wahl der Phasen in (7) allgemein akzeptiert ist, gibt es für die D-Matrizen leider keine einheitliche
Konvention. Bei der Verwendung verschiedener literarischer Quellen sollte man daher zunächst die verwendete
Konvention erötern.
Sei nun Y ein physikalischer Zustand den wir nach einer Basis j jm aus Eigenfunktionen zu J2 und J3 entwickeln.
Y =
j
j jm aHmjL
m
(10)
Die a jm bezeichnen die Entwicklungskoeffizienten. Eine Drehung R œ SO(3) induziert eine unitäte Transformation
a £ m£ = ‚ Dm£ m HRL aHmjL
H jL
H jL
(11)
m
H jL
H jL
H jL
H jL
der Vektoren ÷a” = (a j , a j-1 , ... ,a-j+1 , a- j LT , also der Entwicklungskoeffizienten. Damit der physikalische Zustand Y
unter der Drehung invariant bleibt, transformiert sich die Basis daher mit der zu D(R) kontragredienten Abbildung
HD-1 L (R) . Die ausfürliche Erläuterung hierzu findet man im Vortrag von Andreas Müller.
Es gilt somit
T
‚ j m£ j £ jm£ a £ m£ =
H jL
jm
j jm aHmjL
H jL
Da D(R) unitär ist, ist die Inverse gleich der Adjungierten. Durch nochmalige Transposition erhält man Dm£ m * und die
Basis transformiert sich durch
j £ jm£ = ‚
HjL
m
Dm £ m
* Hy, q, fL j jm
(12)
Genausogut könnte man die Basis durch D und die Entwicklungskoeffizienten durch D* transformieren. Wie bereits
erwähnt, gibt es hierbei keine einheitliche Regelung. Hat man jedoch eine Wahl getroffen, so ist mit (11) und der
Condon-Shortley-Konvention die Phase der D-Matrizen eindeutig festgelegt.
H jL
(q) einführen, betrachten wir jedoch zunächst zwei Beispiele.
Bevor wir die allgemeine Formel zur Berechnung von dnm
Das erste betrifft den Unterraum mit j = 0. Dieser besteht aus einem Zustand bzw. einem Operator, der ein Skalar
bezügl. Drehungen ist und daher unter Anwendung der D-Matrix invariant bleibt. Es gilt also trivialerweise DH0L =1.
Das zweite Beispiel ist besonders interessant.
D-Matrizen im Unterraum
H1ê2L
Zunächst gilt m œ {-1/2,1/2}. Die Erzeugenden der Drehungen bzw. die Komponenten des Drehimpulsoperators
ergeben sich sofort aus den Formeln (7)
Eulersche Winkel, Drehmatrizen und Spin.nb
5
è!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
X m£ » J1 » m \ = ÅÅÅÅ12 1 ê 2 H1 ê 2 + 1L - H-1 ê 4L (dm£ ,m+1 + dm£ ,m-1 ) = ÅÅÅÅ12 (dm£ ,m+1 + dm£ ,m-1 )
X m£ » J2 » m \ = -i (m£ - m) X m£ » J1 » m \ = ÅÅ2iÅÅ (-dm£ ,m+1 + dm£ ,m-1 )
X m£ » J3 » m \ = ÅÅÅÅ12 Signum(m) dm£ ,m
und somit
i 0 1 yz
J1 = ÅÅÅÅ12 jj
z
k1 0 {
i 0 -i yz
J2 = ÅÅÅÅ12 jj
z
ki 0 {
i 1 0 yz
J3 = ÅÅÅÅ12 jj
z
k 0 -1 {
(13)
Lässt man den Faktor 1/2 außer Acht, so sind uns diese Matrizen bereits als Pauli-Matrizen sk bekannt. Bei der
Berechnung von d H1ê2L (q) nutzen wir nun aus, dass
sk n = 9
12 für n gerade
sk für n ungerade
Somit erhält man über die Exponentialreihe
dH1ê2L (q) = exp(i ÅÅÅÅ2q s2 )
H-1L
1
Å H ÅÅÅÅq L + ...+ ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅ H ÅÅÅÅq L
= 12 [ 1 - ÅÅÅÅ
2! 2
H2 pL! 2
=
12 cos( ÅÅÅÅ2q
)+i
2
p
s2 sin( ÅÅÅÅ2q
i cosHq ê 2L sinHq ê 2L
dH1ê2L (q) = jj
k sinHq ê 2L cosHq ê 2L
2p
H-1L
1
+ ...] + i s2 [ ÅÅ2qÅÅ - ÅÅÅÅ
ÅÅ H ÅÅÅÅq L + ... + ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅÅ H ÅÅÅÅq L
3! 2
H2 p+1L! 2
3
p
2 p+1
+ ...]
)
yz
z
{
Die vollständige D-Matrix ergibt sich dann aus (9) zu
(14)
i cosHq ê 2L e i Hy + fL ê 2 sinHq ê 2L e i Hy - fL ê 2
DH1ê2L (y, q, f) = jj
k sinHq ê 2L e -i Hy - fL ê 2 cosHq ê 2L e -i Hy + fL ê 2
yz
z
{
(15)
Diese hat eine interessante Eigenschaft. Führen wir eine komplette DRehung um 3 durch, d.h. setzen wir
beispielsweise y = 0, q = 0, f = 2 p (oder irgendeine beliebige Komposition mit q = 0 und y + f = 2 p), dann erhält man
0
i eip
DH1ê2L (0, 0, 2p) = jj
k 0 e -i p
0 y i -1 0 y
yz ij cosHpL
zz = jj
zz = -12
z= j
cosHpL { k 0 -1 {
{ k 0
also minus die Identität.
Zwei vollständige Drehungen vermöge DH1ê2L (0, 0, 4p) führen hingegen in die Indentität zurück.
Anschaulich gesprochen bewirkt eine Drehung des eingenommenen Zustands um 360o ein Vorzeichenwechsel
desselbigen. Diese verblüffende Eigenschaft tritt in allen Unterräumen zu halbzahligem j auf. Der Vorzeichenwechsel
kann in der Praxis tatsächlich verifiziert werden, wenn man den sogenannten Spin eines Elementarteilchens genauer
unter die Lupe nimmt. Wir kommen später darauf zurück.
allgemeine Formel zur Berechnung von dH jL HqL
Die Herleitung der allg. Formel ist mit größerem Aufwand verbunden und soll an dieser Stelle übersprungen werden. Es
ist
è!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Hj + nL! Hj - nL! Hj + mL! Hj - mL!
ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ Hcos ÅÅÅÅ2q L
dnH jLm (q) = ‚ H-Lp ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
Hj - n - pL! Hj + m - pL! p! Hp + n - mL!
p
2 j-n+m-2p
Hsin ÅÅÅÅ2q L
2 p + n -m
(16)
Hierbei handelt es sich um eine endliche Summe über p. Um dies einzusehen, machen wir einen kleinen Exkurs über die
Gammafunktion, die gerade die analytische Fortsetzung der Fakultät auf ganz wiedergibt. Die Fakultäten im Nenner
Eulersche Winkel, Drehmatrizen und Spin.nb
6
von (16) lassen sich ja über G(n+1) = n! berechnen.
Ein möglicher Ausgangspunkt der Gammafunktion ist das Eulersche Integral
Ÿ
¶
G(z) =
0
dt t z-1 e-t
Ÿ
zœ
(17)
Mittels partieller Integration bestätigt man, dass tatsächlich
¶
G(n+1) =
dt tn e-t = n!
0
gilt. Das Integral (17) konvergiert jedoch nur, falls Re{z}> 0 und kann daher noch nicht die gesuchte analytische
Fortsetzung der Fakultät auf ganz sein. Jedoch konvergiert das Integral über [1,¶) für alle z ohne Einschränkung des
Realteils auf der rechten Hälfte der komplexen Ebene. Wir spalten daher das Integral in zwei Teile und zwar in ein
solches über [0,1] und eines über [1,¶). Es ist
Ÿ
1
dt t
z-1 -t
e
=
0
H-Lk
‚k=0 ÅÅÅÅk!ÅÅÅÅÅÅ
¶
Ÿ
1
Ÿ
H-L
1
dt t k + z-1 = ‚
ÅÅÅÅ
ÅÅÅÅÅÅ ÅÅÅÅÅÅÅÅ
ÅÅÅÅ
k=0 k! z + k
¶
0
k
Die gesuchte analytische Fortsetzung lautet somit
G(z) = ‚
¶
k=0
H-L
1
ÅÅÅÅ
ÅÅÅÅÅÅ ÅÅÅÅÅÅÅÅ
ÅÅÅÅ +
k! z + k
k
¶
dt tn e-t
1
(18)
Die Gammafunktion G(z) ist somit eine meromorphe Funktion und hat an den Punkten z = – k, k œ 0 Pole erster
Ordnung. Folglich besitzt die Umkehrfunktion 1/ G(z) an diesen Punkten Nullstellen. Somit verschwinden in (16) alle
Summanden, für die eine der Klammerterme im Nenner einen negativen Wert annimmt. Da in diesen Termen p sowohl
mit positiven als auch mit negativen Vorzeichen auftritt, ist der Wert von p nach oben und nach unten beschränkt.
Schließlich kann man aus (16) noch einige Symmetrieeigenschaften ablesen:
dmH jLn (q) = H-Ln-m dnH jLm (q)
H jL
(q) = H-Ln-m dmH jLn (q)
d-n,-m
H jL
(q) = H-L j-n dnH jLm (p - q)
dn,-m
(19)
Bei ganzzahligen Werten von j, wobei j als l bezeichnet wird, besteht ein enger Zusammenhang zu den
Kugelflächenfunktionen, nämlich
2l+1
ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅ DHlL
Yl m (q, f) = "#############
0,m (0, q, f)
4p
Spin und magnetisches Moment
Der Spin ist eine innere Eigenschaft, da er, im Gegensatz zum Bahndrehimpuls l nicht vom Bewegungszustand der
Elementarteilchen abhängt. Spin-1/2-Teilchen, die Fermionen sind, sind beispielsweise das Elektron, das Myon, das
Proton und das Neutron. Sie sind daher in die Spinor-bzw. Fundamentaldarstellung der Drehgruppe einzuordnen, die
zugehörigen Operatoren leben somit im Unterraum H1ê2L . Hält man sämtliche Bewegungsmerkmale dieser Teilchen
fest, so können sie in den Zuständen † 1/2, +1/2 \ und † 1/2, –1/2 \ auftreten, von denen der erste der in positiver
3-Richtung ausgerichteten, der zweite der in negativer 3-Richtung ausgerichteten Spin beschreibt.
Physikalisch gesehen beschreibt der Spin ein magnetisches Moment m, das proportional zum sogenannten Bohrschen
Magneton mHiL
B des Teilchens (i) ist:
m = g HiL mHiL
B 1/2
wobei
mHiL
B := e Ñ / (2 mi c)
Hierbei ist g HiL das gyromagnetische Verhältnis welches auf Wechselwirkungen innerhalb des Atoms basiert. Für
elektrisch geladene Teilchen erhält man in erster Näherung den Wert 2. Wir wollen hierauf später kurzr eingehen.
(20)
Eulersche Winkel, Drehmatrizen und Spin.nb
7
Die Ladung ist im Falle des Elektrons e- und des Myons m- natürlich e = – †e§ und im Falle des Protons, des Positrons
e+ sowie des positiven Myons m+ e = †e§. Der Faktor 1/2 ist gerade mmax . Der selbstadjungierte Operator, dem man
dem magnetischen Moment zuordnet, ist somit
m = gHiL mHiL
B
s
(21)
Hierbei ist die Observable m gerade der größte Erwartungswert des obigen Operators.
Machen wir nun einen kleinen Ausflug in die Elektrodynamik und betrachten die Bahnbewegung eines im Atom
gebundenen Elektrons:
Das Magnetische Moment M ist allg. definiert als das Raumintegral der Magnetisierungsdichte m(x), die ihrerseits
durch die elektrische Stromdichte j(x) bestimmt wird:
M=
Ÿd
3
x m(x)
wobei
1
m(x) = ÅÅÅÅ
ÅÅÅÅ x × j(x)
2c
Die Stromdichte wird durch folgenden selbstadjungierten Operator dargestellt:
Ñ e
j(x) = ÅÅÅÅ
ÅÅ ÅÅÅÅÅ @y* “y – H“yL* yD
2i m
Für den Bahndrehimpuls definiert man
l := ÅÅÅÅ1i x × “
und man erhält
eÑ
eÑ
m(x) = ÅÅÅÅÅÅÅÅÅÅÅÅ ÅÅÅÅ1i x × @y* “y – H“yL* yD = ÅÅÅÅÅÅÅÅÅÅÅÅ @y* l y + Hl yL* yD
4mc
2mc
Hierbei möchte ich auf den Vorzeichenwechsel in der Klammer hinweisen der schlicht durch das komplexe Konjugieren
des Operator l entsteht. Darüberhinaus ist l selbstadjungiert, beide Terme innerhalb der Klammer sind
daher identisch und, wenn wir über den gesamten Raum integrieren, gleich dem Erwartungswert von l im Zustand y.
eÑ
M = ÅÅÅÅÅÅÅÅÅÅÅÅ X l \ ª mB X l \
2mc
Für den selbstadjungierten Operator erhält man entsprechend
ml = mHiL
B
l
(diesmal ohne gyromagnetisches Verhältnis)
(22)
Das Bohrsche Magneton ist somit die natürliche Einheit für magnetische Momente der Elementarteilchen. Man sieht
jetzt auch, dass Spin und Bahndrehimpuls physikalisch gleich beschaffen sind. Mann kann sie daher zum Gesamtdrehimpulsoperator
j = l + s aufaddieren.
Die magnetische Orientierungsenergie, welche die Wechselwirkung zwischen manetischem Moment und einem
äußeren Magnetfeld B beschreibt, ist gegeben duch den Term – M · B. Sei H0 der Hamiltonoperator, der das Atom
beschreibt. Dieser ändert sich in Anwesenheit eines äußeren Feldes zu
H = H0 –
eÑ
ÅÅÅÅÅÅÅÅ
ÅÅÅÅ l · B
2mc
(23)
Allerdings treten noch weitere Wechselwirkungen auf, die im oben genannten Hamilton-Operator noch nicht
berücksichtigt wurden. Der Spin wechselwirkt ebenso mit dem äußeren Feld wie mit dem Bahndrehimpuls, die
Wechselwirkung mit dem aüßeren Feld ist proportional zu s · B, die Kopplung mit dem Bahndrehimpuls ist proportional
zu l · s. Der Hamilton-Operator ergibt sich also als
H = H0 –
eÑ
ÅÅÅÅÅÅÅÅ
ÅÅÅÅ l · B
2mc
2
Ñ
eÑ
dUHrL
– g ÅÅÅÅÅÅÅÅÅÅÅÅ s · B – ÅÅÅÅÅÅÅÅ2ÅÅÅÅÅ2ÅÅÅ ÅÅ1rÅÅ ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅ l · s
dr
2mc
2m c
(24)
Hierbei geben der zweite und dritte Term die Wechselwirkung des Bahndrehimpulses bzw. Spins mit dem aüßeren Feld
wieder, der vierte Term beschreibt die Spin-Bahn-Kopplung, die sich im Experiment durch die sogenannte Feinstruktur
Eulersche Winkel, Drehmatrizen und Spin.nb
8
in den Spektrallinien zeigt. Um den letzen Term zu erklären, bedarf es einer relativistischen Betrachtung der
Quantenmechanik. Der auftretende g-Faktor (Landé-Faktor) wird in der nicht-relativistischen QM bei e- als 2
postuliert, in der relativistischen Theorie zeigt sich allerdings, das g=2 kein Postulat oder eine Abschätzung ist, sondern
direkt aus der Theorie folgt.
Ausblick
Der Elektronenspins und die verbundene Wechselwirkung mit einem inhomogenen äußeren Feld wurde durch Stern und
Gerlach entdeckt, er spielt eine große Rolle im Verständnis des Aufbaus der Elektronenhülle. Das von Pauli 1940
entdeckte Spin-Statistik-Theorem liefert einen Zusammenhang zwischen Spin und der Statistik, der Vielteilchensysteme
unterworfen sind. Aus der Vertauschungsrelation für Fermionen, die das Spin-Statistik-Theorem fordert, geht
unmittelbar das Pauli-Prinzip hervor.
Eine weitere Anmerkung ist zum Landé-Faktor zu machen: In der relativistischen QM lässt sich zwar zunächst der Wert
g=2 für e- finden, er ist aber keineswegs eine Konstante, sondern kann durch Wechselwirkungen, denen das Teilchen
unterworfen ist, abgeändert werden. Für unser Beispiel eines e- ist das die Wechselwirkung mit dem Maxwellschen
Strahlungsfeld, in der sich der Faktor durch eine Potenzreihe annähern lässt. Die niedrigste Näherung hierbei lautet
ge º 2 + ÅÅapÅÅ
(25)
Noch unberücksichtigt bleiben die Wechselwirkungen des Kernspins mit dem äußeren Feld und mit dem Spin des e- ,
im Experiment zeigt sich eine weitere Aufspaltung, die man als Hyperfeinstruktur bezeichnet. Ebenso wie das Elektron
trägt der Kern den Spin 1/2 und daher auch ein damit verbundenes magnetisches Moment, dessen Betrag allerdings um
etwa drei Größenordnungen niedriger wie der des Elektrons ist, daher lässt die Aufspaltung schwieriger nachweisen.
Nachweis des Vorzeichenwechsels durch Neutroneninterferometrie
Da der Spin ein magnetisches Moment beschreibt, kann er durch äußere Magnetfelder beeinflusst werden. Der
zugehörige Hamiltonoperator lautet
Hs = -g
eÑ
ÅÅÅÅÅÅÅÅ
ÅÅÅÅ s · B
2mc
(*)
Dieser hängt nicht explizit von der Zeit ab. Betrachten wir nun die zeitliche Entwicklung des quantenmechanischen
Systems: Eine Lösung y(t,x) erfüllt die Schrödingergleichung
†
i Ñ y (t, x) = H y(t, x)
Für eine infinitesimale Zeitdifferenz entwickeln wir y nach der Zeit
i
dy
ÅÅÅÅ À Ht - t0 L = (1 – ÅÅÅÅ H (t – to )) y(t0 , x)
y(t, x) º y(t0 , x) + ÅÅÅÅ
dt
Ñ
t0
Für eine endliche Zeitdifferenz (t – to ) können wir die zeitliche Evolution als Aneinanderreihung vieler solcher Schritte
betrachten und wir erhalten mit Hilfe der Gaußschen Formel
n
i
i
Ht – to L
ÅÅÅÅÅÅ N = exp[– ÅÅÅÅ H (t – to )] ª UHt, t0 L
lim J1 – ÅÅÅÅ H ÅÅÅÅÅÅÅÅ
n
Ñ
Ñ
nض
Der unitäre Operator U Ht, t0 L beschreibt somit die zeitliche Entwicklung des quantenmechanischen Zustands als unitäre
Abbildung der Anfangsverteilung
y(t0 , x) auf die Verteilung y(t , x) zu einer späteren bzw. früheren Zeit.
y(t , x) = UHt, t0 L y(t0 , x)
Eulersche Winkel, Drehmatrizen und Spin.nb
Desweiteren genügt es selbst der Schrödingergleichung mit der Anfangsbed. UHt0 , t0 L = 1
†
i Ñ U Ht, t0 L = H U Ht, t0 L
Betrachten wir z.B. lediglich die 3-Komponente des B-Feldes, so ist mit (*) und t0 = 0
i
eB
s3
U(t, 0) = exp[– ÅÅÅÅ H t ] = exp[ i ÅÅÅÅ
ÅÅÅ w t] wobei wir w := g ÅÅÅÅÅÅÅÅÅÅÅÅ gesetzt haben.
2
Ñ
2mc
Setzen wir jetzt w t = f, so erhalten wir gerade die Darstellung der Drehung um die 3-Achse. Somit ist klar, dass ein
äußeres Magnetfeld Spinpräzession verursacht. Diese Tatsache macht man sich zunutze, um den Vorzeichenwechsel des
Zustands bei einer Drehung um 2 p nachzuweisen. Zunächst einmal sollte man sich jedoch darüber im Klaren sein, dass
das Vorzeichen eines quantenmech. Zustands reine Konvention ist. Nehmen wir an, wir könnten die Zeit anhalten und
bei allen Zuständen im Universum die Vorzeichen umkehren.
Wenn wir die Zeit dann weiterlaufen lassen, hätte sich physikalisch nicht das geringste geändert. Eine phys. relevante
Beobachtung macht man nur dann, wenn man die Wechselwirkung von Zuständen untereinander betrachtet, von denen
einer sein Vorzeichen ändert. Dies geschieht bei der sogenannten
Neutronen-Interferometrie:
Bei diesem Experiment wird ein Neutronenstrahl in zwei Teilbündel A und B geteilt, B wird durch ein Magnetfeld B
geleitet und mit dem anderem Teilbündel wieder zusammengeführt. Beim Zusammentreffen kommt es zur Interferenz
der Zustandsamplituden. Der Zustand in B erfährt somit einen Phasensprung exp[¡ w T /2] wobei T die Zeit ist, in der
das Neutron sich im Magnetfeld befindet. Im Versuch ist T konstant (die Neutronen haben im Mittel stets die selbe
Geschwindigkeit). Jedoch ändert man die Präzessionsfrequenz durch Variation der Feldstärke.
¡w T
ÅÅÅÅÅ + d ) wobei d die Phasendifferenz der beiden
Die Intensität in der Interferenzregion ist proportional zu cos( ÅÅÅÅÅÅÅÅ
2
Amplituden cA und cB (†B§=0) bezeichnet.
Es sei d die Länge des Weges des Neutronenstrahls durch das Magnetfeld. Der Abstand
zwischen 2 Maxima berechnet sich mit w = 2p / T durch
g e DB
4p
4p pc
4p mc
4p hc
ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅ = ÅÅÅÅ
ÅÅÅÅ
bzw.
DB = ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅ = ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅ = ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅ Å
geT
ged
g eld
mc
T
Hierbei haben wir angenommen, dass der Zustand erst nach einer 4p-Rotation in seine Ausgangskonfiguration
zurückkehrt. Wäre die Theorie falsch, so würde DB lediglich halb so groß sein. Das Ergebnis konnte jedoch in den
siebziger Jahren experimentell bestätigt werden.
Literatur
- F.Scheck, Theoretische Physik, Band II: Nichtrelativistische Quantentheorie, Springer, Berlin, Heidelberg, 2000
- J.J. Sakurai, Advanced Quantum Mechanics, Addison Wesley, Reading, 1967
- C. Cohen-Tannoudji, Mécanique Quantique I+II, Hermann, Paris 1977
- P.G.J. van Dongen, versch. Skripte zur Quantenmechanik, Mainz, 1998-2004
9