PHG07 h-Bestimmung mit LEDs File

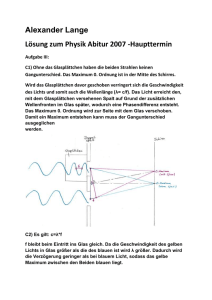
Tabelle 1: Verwaltungsangaben
HTW-Berlin
Fachbereich 1
Physikalisches Praktikum
Bestimmung des Planckschen Wirkungsquantums „h“
mit Hilfe des äußeren photoelektrischen Effekts und LED´s
Namen der
(Studenten)
Zug:
Labor am:
Woche:
Abgabe:
Gruppe:
Prof./Doz:
Tabelle 2: Endergebnisse der Auswertung
Wellenlänge: (nm)
1. LED
611 nm
2. LED
588 nm
3. LED
525 nm
4. LED
505 nm
Frequenz: f (Hz)
Endergebnisse Bremsspannungen: U0 (V)
E 0 = U 0  e (J)
E kin = h  f – W (J)
Elektronenaustrittsarbeit
(theoretisch) W (J)
 3 120  10
– 19
J
Elektronenaustrittsarbeit
(Messergebnis) W(J)
Plancksche Konstante
(theoretisch) h (Js)
6 626  10
– 34
Js
Plancksche Konstante
(Messergebnis) h (Js)
Hinweise: Der verwendete Begriff „ Bremsspannung “ wird in der Literatur auch
mit „ Haltepotential “ bezeichnet.
Für das Symbol der Austrittsarbeit „W“wird in der Exzell-Tabelle von NTL
das Symbol „“ verwendet.
5. LED
472 nm
Messtabelle 3: Ermittlung der Bremsspannungen (Haltepotential) U o (V)
Wellenlängen 
Messzyklus
611 nm
1. LED
588 nm
2. LED
525n m
3. LED
505 nm
4. LED
472 nm
5. LED
Intensität
bei 75%
Intensität
bei 75%
Intensität
bei 75%
Intensität
bei 75%
Intensität
bei 75%
1.
2.
3.
4.
5.
U 75
Mittelwert
Mittelwert
Mittelwert
Mittelwert
Mittelwert
Intensität
bei 50 %
Intensität
bei 50 %
Intensität
bei 50 %
Intensität
bei 50 %
Intensität
bei 50 %
Mittelwert
Mittelwert
Mittelwert
Mittelwert
Mittelwert
Bestwert
Beswert
Bestwert
Bestwert
Bestwert
Teilergebnis
Messzyklus
6.
7.
8.
9.
10.
U 50
Teilergebnis
U 75 + U 50
------------------------2
Endergebnis
HTW-Berlin- Labor Physikalisches Praktikum
Laborleiter Prof. Dr. Frank-U. Fink
Versuchsanleitung
Bestimmung des Planckschen Wirkungsquantums h
mit Hilfe des äußeren photoelektrischen Effekts und (LEDs)
1.) Der historische Hintergrund des Experiments:
Im Jahre 1887 untersuchte der deutsche Physiker Heinrich Herz die Bildung und Ausbreitung
elektromagnetischer Wellen. Er befasste sich mit der Funkenbildung zwischen elektrisch geladenen Platten und entdeckt, dass die Stärke und die Anzahl der Funken zunahmen wenn die Platten mit ultraviolettem Licht bestrahlt wurden. Im Jahre 1888 entdeckte ein anderer deutscher
Physiker, Wilhelm Hallwachs, dass eine negativ geladene Metallplatte aus Zink wesentlich
schneller Ihre Ladung verliert, wenn sie mit ultraviolettem Licht bestrahlt wird. Er erklärt das
Phänomen durch die Emission negativ geladener Teilchen.
Zwölf Jahre später entdeckte der deutsche Physiker Philipp Eduard Anton Lenard, dass die
Zündspannung für elektrische Lichtbögen zwischen zwei Elektroden erheblich niedriger wird
wenn die negative Elektrode mit ultraviolettem Licht bestrahlt wird. Er bewies außerdem, dass
es sich bei den Teilchen, die durch die Bestrahlung der negativen Elektrode emittiert werden,
um Elektronen handelt. Im Weiteren versuchte Lenard die Energie zu messen, die man braucht,
um Elektronen durch Bestrahlung aus fotosensitiven Platten herauszuschlagen. Er machte die
sensationelle Entdeckung, dass mit wachsender Intensität der Strahlung zwar die Anzahl der
herausgeschlagenen Teilchen zunimmt, nicht aber deren kinetische Energie. Er stellte auch fest,
dass durch „ langwellige “ Strahlung, unabhängig von der Höhe der Intensität, keine Elektronen
von den Platten emittiert werden. Die Ergebnisse der Experimente von Lenard konnten durch
die klassische Maxwellsche Theorie des Lichtes nicht erklärt werden.
Dieser - so genannte Photoeffekt - stellte Anfang des 20.Jahrhunderts, als man die Physik für
fast abgeschlossen hielt, eines der letzten Rätsel dar. Man konnte sich nicht erklären, wieso
Licht erst ab einer bestimmten Frequenz (unterhalb einer bestimmten Wellenlänge) Elektronen
aus bestimmten Metallen schlagen kann, denn Licht ist in der klassischen Physik eine elektromagnetische Welle, deren Energie proportional zu ihrem Amplitudenquadrat anwächst. Für das
Auslösen eines Elektrons aus einem Metall ist eine gewisse Energie notwendig. Nach der klassischen Theorie des Lichtes müsst man also die Intensität, (die Amplitude) der Lichtwelle mit
der man das Metall bestrahlt, entsprechend hoch einstellen, um Elektronen herauszuschlagen.
Das sollte von der gewählten Wellenlänge immer funktionieren.
Die Experimente von Hertz, Hallwachs und Lenard führten zu Resultaten, die der Wellentheorie widersprachen. Unterhalb einer Grenzfrequenz, bzw. oberhalb einer Wellenlänge (für jedes
Metall eine andere) kann die Intensität der Bestrahlung beliebig erhöht werden, ohne das Elektronen aus diesem Metall herausgeschlagen werden.
Überschreitet man diese Grenzfrequenz, werden (schon bei niedrigeren Intensitäten)
Elektronen herausgeschlagen. Je größer dann die Intensität, desto mehr Elektronen werden
ausgelöst. Die Energie der Elektronen steigt nicht! mit der Intensität des Lichtes aber mit
seiner Frequenz.
Die Erklärung dieses Phänomens konnte mit der klassischen Theorie gar nicht gelingen. 1905
gelang Einstein die genial einfache, theoretische Beschreibung dieses Effekts mit Hilfe der von
Max Planck eingeführten Quantentheorie. Er nahm nun an, dass Licht aus Teilchen besteht,
den so genannten Photonen. Die Energie E dieser Photonen (der Lichtquanten) ist direkt
proportional zu ihrer Frequenz f sowie der Betrag ihres Impulses p indirekt proportional zur
Wellenlänge λ :
E = hf
und
h
p = --
Dabei ist die Proportionalitätskonstante h das „ Planksche Wirkungsquantum “.
Das bedeutet, dass die Energie E in Form von elektromagnetischer Strahlung nur in kleinen
Paketen, in Quanten, abgegeben werden kann. Diese Mindestgröße E0 ist von der Frequenz der
Strahlung abhängig.
Nach der Quantentheorie ist elektromagnetische Strahlung weder nur eine Welle noch nur ein
Teilchen. In manchen Experimenten (Beugung, Reflexion, Brechung) weist sie typische
Welleneigenschaften auf und in anderen (Photoeffekt, Comptoneffekt) weist sie
Teilcheneigenschaften auf. Dies nennt man den Welle-Teilchen-Dualismus. Die
mathematische Beschreibung dieses Dualismus liefert die Quantenmechanik.
Einstein erhielt im Jahr 1922 für die quantenmechanische Erklärung des Photoeffekts ( nicht
für die Aufstellung der Relativitätstheorie) den Nobelpreis für Physik.
Der Physiker Millikan, der von der Erklärung Einsteins nicht überzeugt war, suchte
experimentell nachzuweisen, dass die Quantentheorie des Lichtes nicht richtig ist. Zu seiner
eigenen Verwunderung musste er feststellen, dass Einsteins Theorie richtig war. Dabei konnte
er die Planksche-Konstante h experimentell bestimmen. Für seinen Beitrag zur Erforschung
des photoelektrischen Effekts, und die Bestimmung der Elementarladung e von Elekrtonen
e = 1 6021  10
– 19
C
erhielt er 1923 den Nobelpreis für Physik.
Das Plancksche Wirkungsquantum h ist eine Naturkonstante. Sie hat den Wert:
h = 6 62606957  29   10
– 34
Js
Es hat die Dimension: Wirkung = Energie * Zeit.
Im Laborversuch sollen Sie das Planksche Wirkungsquantum h experimentell bestimmen. Der
Effekt, der im Experiment auftritt, ist der äußere Photoeffekt. Bei diesem werden Elektronen
durch unterschiedliche Lichtstrahlung aus einer Metalloberfläche herausgelöst. Neben dem
äußeren photoelektrischen Effekt gibt es noch zwei Arten des inneren photoelektrischen Effekts, der in Halbleitern dazu führt, dass sie leitend werden (Photoleitung), bzw. die Umwandlung von Strahlungsenergie in elektrische Energie bewirkt (photovoltaischer Effekt). Es
existiert noch eine vierte Art des Photoeffekts die Photoionisation, bei der Elektronen durch
elektromagnetische Strahlung aus Atomen herausgelöst werden.
Der äußere Photoeffekt kann sehr gut erklärt und demonstriert werden, während die Verhältnisse in Halbleitern wesentlich kompliziertere Annahmen erfordern.
Der äußere Photoeffekt ist für Studenten leichter nachvollziehbar. Sie werden noch den wichtigen Begriff der Austrittsarbeit W eines Elektrons kennen lernen.
(Beim inneren Photoeffekt spielt das Bändermodell und die Bandlücke zwischen Valenz- und
Leitungsband noch eine wichtige Rolle).
2.) Versuchsaufbau und Theorie des Experimentes
äußerer photoelektrischer Effekt
Unter der zylinderförmigen Abdeckung (1) des Gerätes befindet sich eine Photozelle, die aus
einer Kathode und einer ringförmigen Anode besteht. Die Oberfläche der Kathode ist aus
Cäsium, das aufgedampft wurde. Bei eingeschaltetem Gerät liegt zwischen den beiden
Elektroden eine Spannung, die über die Regler (5) und (6) grob und fein verändert werden
kann.
Zur Bestimmung des Plankschen Wirkungsquantums h verwenden Sie LEDs mit
verschiedenen Wellenlängen (Farben). Das ausgesendete Licht der LEDs tritt durch die
Öffnung der ringförmigen Anode und trifft auf die Oberfläche der Kathode.
Der physikalische Effekt ist folgender; Wird ein Elektron der Cäsiumatome von einem Photon
getroffen, gibt das Photon seine gesamte Energie ( E = h  f ) an dieses ab. Ein Teil der
Energie wird dazu benötigt das Elektron herauszuschlagen (Austrittsarbeit W). Der jeweilige
Rest der Energie steht dem „ freien“ Elektron als kinetische Energie Ekin zur Verfügung.
E Photon = h  f = W + E kin
Die Austrittsarbeit W ist eine materialspezifische Größe und somit für jedes Metall anders. Sie
hängt außerdem von der Temperatur des Metalls ab. Cäsium eignet sich gut als
Kathodenoberflächenmaterial, weil seine Elektronen an der Oberfläche eine niedrige
Austrittsarbeit benötigen.
– 19
J bzw. 2,0*e bei
Die Austrittsarbeit für Cäsium beträgt 3 120  10
Zimmertemperatur. Durch das Licht, die die LEDs aussenden werden Elektronen aus der
Cäsiumoberfläche der Photodiode herausgeschlagen und es fließt ein Elektronenstrom von der
Kathode zur Anode. Dieser wird über ein Nano-Amperemeter (3) gemessen bzw.
nachgewiesen.
Zwischen Anode und Kathode liegt eine veränderliche Gegenspannung . Durch diese werden
die herausgeschlagenen Elektronen wieder abgebremst. Die sogenannte Bremsspannung U0 ,
Haltepotential genannt, kann erhöht werden, bis kein Strom mehr bis zur Anode fließt.
In diesem Fall, „verlieren“ die freien Elektronen ihre gesammte kinetische Energie.
Aus dieser Bremsspannung ergibt sich folgerichtig die Energie, die das freie Elektron besitzt:
E0 = e  U0
Dabei ist e = 1 6021  10
– 19
C die Elementarladung.
Wenn keine Elektronen mehr die Anode erreichen können, der Elektronenstrom zum Stillstand
kommt, also Null wird, entspricht e  U 0 genau der kinetischen Energie der Elektronen.
Fassen wir analog einer Geradengleichung (y = mx + n ) zusammen:
e  U 0 = E kin = h  f – W
Da h als auch W konstant und somit von Frequenz f, bzw. der Wellenlänge des jeweiligen
Photons unabhängig sind, kann man die Energie e  U 0 gegen die Frequenz f in ein
Diagramm eintragen. Die Energie - Frequenz Paare müssen auf einer Geraden liegen.
e .U0 (eV)
*
h .f - W
*
*
*
*
f (10+14 Hz)
Beachte: Für jedes Kathodenmaterial ist der y-Achsenabschnitt der entsprechenden Geraden
anders, der Anstieg der Geraden ist jedoch vom Kathodenmaterial unabhängig.
Die Sachverhalte, die Sie mit dem Experiment lernen sollen sind zusammengefaßt folgende:
Die kinetische Energie der Elektronen ist von der Intensität (Helligkeit) des LED-Lichtes
unabhängig. Sie hängt nur von der Frequenz des Lichtes ab.
Lediglich die Zahl der freigesetzten Elektronen hängt von der Intensität ab.
Unterhalb einer bestimmten Grenzfrequenz werden überhaupt keine Elektronen mehr
ausgelöst, unabhängig von der Intensität des eingestrahlten Lichtes.
Wenn Elektronen freigesetzt werden, beginnt der Vorgang ohne Zeitverzögerung mit dem
Beginn der Bestrahlung, auch bei geringen Bestrahlungsintensitäten.
Diese Feststellungen sind mit dem Modell „Licht als Welle“ nicht zu erklären.
Die von einer Welle transportierte Energie ist dem Amplitudenquadrat, also der Intensität, proportional. Die Energie der freigesetzten Elektronen hängt aber gerade nicht von der Intensität
ab.
Unterhalb einer Grenzfrequenz des bestrahlenden Lichtes werden überhaupt keine Elektronen
aus den bestrahlten Atomen freigesetzt, selbst wenn die Bestrahlungsintensität maximal gestei-
gert wird, weil ihre Licht-Teilchen-Energie (Photonenenergie) die notwendige Austrittsarbeit
an den Elektronen im Atom nicht mehr leistet.
Auch bei geringsten Bestrahlungsintensitäten sind mit Beginn der Bestrahlung sofort freigesetzte Elektronen nachweisbar, wenn ihre Teilchen-Energie ausreicht, um die Austrittsarbeit zu
leisten.
Beschreibung der Bedienelemente des Gerätes:
1
2
9
5
10
4
3
88
6
7
(1) Schutzabdeckung für die Photozelle
(2) LED Aufnahmerohr
(3) Nano-Amperemeter. Empfindliches Instrument zur Messung des Photostromes
(4) Voltmeter zur Messung der Bremsspannung U0
(5) Drehknopf zur groben Einstellung der Bremsspannung
(6) Drehknopf zur feinen Einstellung der Bremsspannung
(7) Drehknopf zur Einstellung der Intensität der Lichtquellen
(8) Buchse für die Lichtquellen
(9) Buchse für die Stromversorgung
(10) LEDs mit Verbindungskabel
4.) Durchführung des Experiments:
Beim Experiment werden die Bremsspannungen der fünf zur Verfügung stehenden
Wellenlängen 611 nm, 588 nm, 525 nm, 505 nm, 472 nm (LED-Licht) gemessen. Die
Genauigkeit der Messungen und Messergebnisse wird durch Mehrfachmessungen und einer
handwerklich hohen Präzision in den Messzyklen sowie einer statistischer Auswertung
erreicht.
Erst aus Mittelwerten/Bestwerten der empirischen Bremsspannungen wird alles andere
berechnet.
Arbeitsschritte:
1.) Das Gerät wird vom Laborpersonal voreingestellt! Das Gerät ist betriebsbereit.
2.) Intensität der Lichtquellen (7) einstellen.
3.) Eine LED in die Buchse für die Spannungsversorgung (8) stecken.
4.) Die LED-Lichtquelle auf das Aufnahmerohr der Photozelle (2) aufstecken.
5.) Den Feineinstellknopf (6) in die Mittelstellung drehen.
6.) Den Grobeinstellknopf (5) drehen bis der Photostrom im
Nano-Amperemeter 0 wird.
7.) Den Feineinstellknopf (6) drehen um der Photostrom exakt 0 zu setzen.
(Die Digital-Anzeige wechselt zwischen (.000) und (-.000) Nanoamper)
8.) Am Voltmeter (4) angezeigte Bremsspannung U0 in Tabelle 3 notieren.
9.) Wiederholung der Schritte 3 - 7 mit den anderen LEDs. ( ein Messzyklus )
10.) Durchführung weiterer Messzyklen. Die Lehrkraft bitte Fragen!
11.) Messergebnisse aller Messzyklen in Tabelle 3 auswerten.
11a) Mittelwerte/Bestwerte für alle Wellenlängen (5 LEDs) bilden,
11b.) Die ermittelten Bestwerte/Endergebnisse in die vorbereitete Excell-Tabelle
am PC eintragen.
11c.) Die Exzell-Tabelle ausdrucken.
Hinweise: Bei Beginn der Laborübung ca. 3 Minuten abwarten, dann mit der Einstellung
der Bremsspannung beginnt.
Nach allen Messungen bitte die Schutzhaube
über die LED - Aufnahme der Photozelle schieben!
5.) Auswertung:
Am schnellsten ist die Auswertung mit dem Excel-Programm. Dazu tragen Sie die errechneten
Mittelwerte U 0 für 75% Intensität für die jeweiligen 5 Wellenlängen (LEDs) aus Messtabelle
3 in die vorbereitete Exzell-Tabelle am Labor-PC ein. Nun kann die Steigung - damit h - und
der y-Achsenabschnitt - damit W - im Graphen abgelesen werden und es wird im Exzell-Programm mit Hilfe der Methode der linearen Regressionsanalyse der Messfehler berechnet und
ausgegeben. Danach übertragen Sie die Werte bei 50 % Intensität ein, lesen die Werte ab und
vergleichen.
Aufwendiger, weil ohne PC-gestützte Exzell-Tabellenauswertung, gelangen Sie folgendermaßen zum Ergebniss:
5.1) Abschätzung des Ergebnisses:
Gleichungen für zwei Frequenzen f1 und f2 und den entsprechenden Bremsspannungen
U1 und U2 dienen zunächst einer schnellen Abschätzung
e  U1 = h  f1 – W
e  U2 = h  f2 – W
Die Frequenzen erhält man aus den Wellenlängen und der Gleichung f = c/λ, wobei λ die
8
Wellenlänge des LED-Lichtes und c  3  10 m/s die Lichtgeschwindigkeit ist.
Achtung: Die Wellenlängen in Meter! einsetzen (1 nm = 10-9 m.)
Das ist ein Gleichungssystem von 2 Gleichungen mit 2 Variabeln. Wenn man nach h und W
auflöst erhält man:
 U2 – U1 
U 0
---------h = e
= e  ------------------------f
 f2 – f1 
W = h  f1 – e  U1 = h  f2 – e  U2
Diese Methode ist eine Abschätzung. Sie kann zu Abweichungen führen, wenn ein Wert
falsch gemessen wurde. ( Vorschlag: hier bereits die Mittelwerte aus den Messzyklen nutzen)
5.2) Ermittlung eines vollständigen Ergebnisses:
Man kann hierfür den Anstieg einer Ausgleichsgeraden mit Hilfe der Linearen Regression
ermitteln. (Siehe dazu die Anleitungen zur Fehlerrechnung)
 5


f i  e  U i – 5  f  e  U


 i =1

h = ------------------------------------------------------------------------ 5 

f i2 – 5   f  2


 i =1 


W = hf –eU
5
5
 fi
 Ui
5
5
i=1
i=1
Darin ist f = -------------- der Mittelwert der Frequenz und U = ---------------- der Mittelwert
der Bremsspannungen. Die „5“ bedeutet hier, daß mit 5 verschiedenen LEDs die jeweilige
Bremsspannung gemessen wurde.
Wir haben am Anfang der Beschreibung über die Historie der Experimente gesprochen. Kann
man diese Experimente mit dem vorliegenden Versuchsaufbau nachvollziehen? Wenn man das
Experiment, wonach die Bremsspannung von der Intensität der Lichtstrahlung unabhängig ist,
genau nachstellen möchte, wird man feststellen, dass dies mit den LEDs, die Sie verwenden,
nur bedingt möglich ist. Es gibt mehrere Gründe. Der wichtigste ist, dass die Frequenzen des
LED-Lichtes (nach Angabe vom Hersteller) von dem durch die LED fließenden Strom in
gewisser Weise abhängig sind. Im vorliegenden Versuchsaufbau lässt sich das Experiment zur
h-Bestimmung dann präziese genug durchführen, wenn die Intensität des LED-Lichtes auf die
vom Hersteller angegebene Intensität von 75% genau eingestellt ist. Dann entsprechen die
Wellenlängen exakt den Tabellenwerten der verwendeten 5 LEDs.
6.) Literatur:
[1] Versuchsanleitung des Bedienungsgerätes von NTL, Fruhmann GmbH, 7343 Austria
[2] Douglas C. Giancoli, Physik, 3. Auflage, 2010