c d I b a

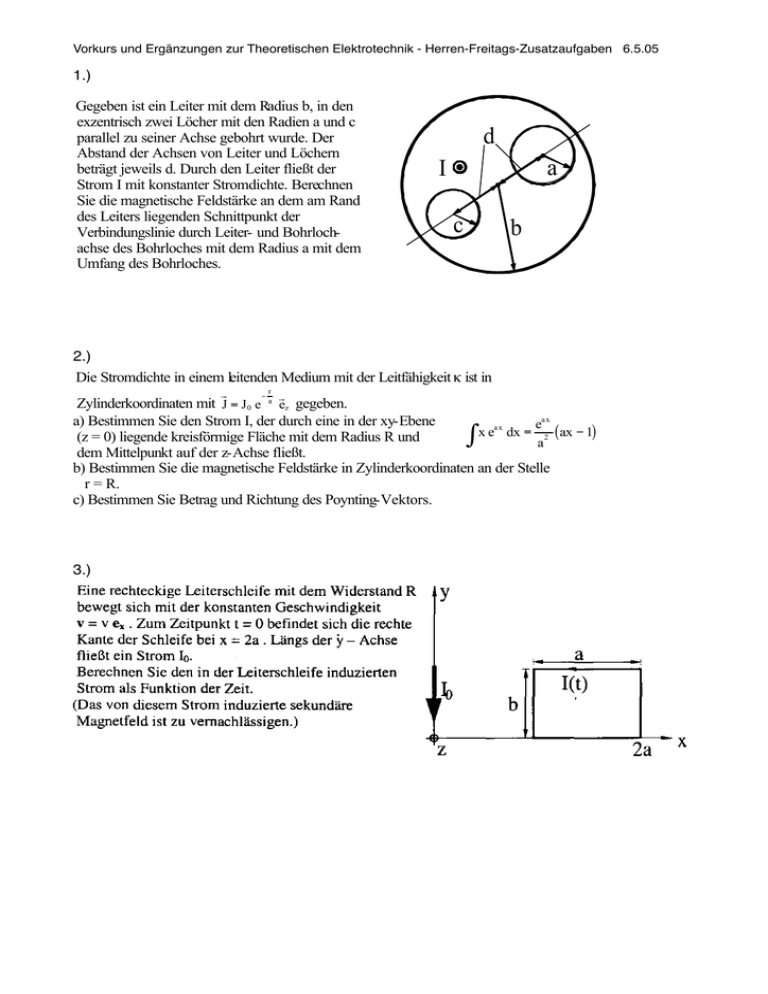
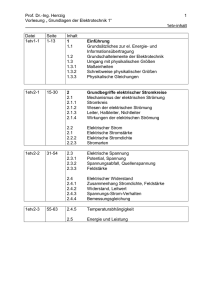
ri
auf der Scheibe befindliche Gesamtladung ?
ra
Vorkurs und Ergänzungen zur Theoretischen Elektrotechnik - Herren-Freitags-Zusatzaufgaben 6.5.05
1.)
3. Gegeben ist ein Leiter mit dem Radius b, in den
exzentrisch zwei Löcher mit den Radien a und c
parallel zu seiner Achse gebohrt wurde. Der
Abstand der Achsen von Leiter und Löchern
beträgt jeweils d. Durch den Leiter fließt der
Strom I mit konstanter Stromdichte. Berechnen
Sie die magnetische Feldstärke an dem am Rand
des Leiters liegenden Schnittpunkt der
Verbindungslinie durch Leiter- und Bohrlochachse des Bohrloches mit dem Radius a mit dem
Umfang des Bohrloches.
d
a
I
c
b
2.)
4. Die Stromdichte in einem leitenden Medium mit der Leitfähigkeit ! ist in
!
"
r
!
Zylinderkoordinaten mit J = J0 e a ez gegeben.
a) Bestimmen Sie den Strom I, der durch eine in der xy-Ebene
ea x
ax
=
" 1)
x
e
dx
2 ( ax
(z = 0) liegende kreisförmige Fläche mit dem Radius R und
a
dem Mittelpunkt auf der z-Achse fließt.
b) Bestimmen Sie die magnetische Feldstärke in Zylinderkoordinaten an der Stelle
r = R.
c) Bestimmen Sie Betrag und Richtung des Poynting-Vektors.
4
5. Eine monochromatische ebene Welle breitet sich im Vakuum mit der
Gechwindigkeit c0 in positive x – Richtung aus. Ihre elektrische
3.)
! !
j k x "# t
!
Feldstärke ist gegeben durch E ( r,t ) = E 0 e ( 0 0 ) ( " ez ) .
a) Zeigen Sie, daß diese Welle die homogene Wellengleichung
! !
1 $2 ! !
% E ( r,t ) " 2 2 E ( r,t ) = 0 erfüllt.
c $t
! !
b) Bestimmen Sie die zugehörige magetische Feldstärke H ( r,t ) über die
Maxwellschen Gleichungen.
6. Ein elektrischer Elementardipol strahlt elektromagnetische Wellen mit einer
Frequenz von 100 MHz ab. Bestimmen Sie die Beträge der Komponenten von
elektrischer und magnetischer Feldstärke in geeigneter Näherung (Begründung) für
eine Entfernung von 10 km mit CE = 100 Am für die Winkel & = 0°, 30°, 90°.
Für das Feld eines elektrischen Elementardipols gilt allgemein:
e"jkr (
1 )
E ' = H r = H & = 0 ; H' = j k CE sin &
*1 +
+
r ,
jkr E r = 2 j k C E Z cos &
2
( 1 ) /
e" j k r . 1
0
+*
+ 1
r 0 jkr , jkr - 1
2
3
;
E& = j k CE Zsin &
2
( 1 ) /
e" jkr .
1
01 +
+*
+ 1
r 0
jkr , jkr - 1
2
3
7. Mit Hilfe der Finite-Differenzen-Methode ist das Potentialfeld in einem
Parallelplattenleiter, der eine Einbuchtung hat, in zwei Iterationsschritten zu
berechnen. Die Knoten 7 und 8 sollen sich noch im homogenen Feld befinden.
Vorkurs und Ergänzungen zur Theoretischen Elektrotechnik - Herren-Freitags-Zusatzaufgaben 6.5.05
4.)
Anhängend Lösungen
(nicht aufbereitet, gerechnet unter Wettbewerbs-Bedingungen, Zeiten am Ende notiert)
Vorkurs und Ergänzungen zur Theoretischen Elektrotechnik - Herren-Freitags-Zusatzaufgaben 6.5.05
Vorkurs und Ergänzungen zur Theoretischen Elektrotechnik - Herren-Freitags-Zusatzaufgaben 6.5.05
Vorkurs und Ergänzungen zur Theoretischen Elektrotechnik - Herren-Freitags-Zusatzaufgaben 6.5.05
Vorkurs und Ergänzungen zur Theoretischen Elektrotechnik - Herren-Freitags-Zusatzaufgaben 6.5.05
Das Verhalten scheint widersprüchlich, da für große v kleine Spannungen entstehen. Dies trifft jedoch nur für große Zeiten zu, während am Anfang große v auch große U erzeugen. Da die gesamte Flußänderung bei einem bestimmten Weg
geschwindigkeitsunabhängig ist, muß eine hohe Änderungsgeschwindigkeit am Beginn mit einer niedrigen am Ende
kompensiert werden:
U(t) in willkürlichen Einheiten:
rot: v = 4, oliv: v = 2, hellblau: v = 1,
violett: v = 0.5, rot2: v = 1000
Vorkurs und Ergänzungen zur Theoretischen Elektrotechnik - Herren-Freitags-Zusatzaufgaben 6.5.05
Vorkurs und Ergänzungen zur Theoretischen Elektrotechnik - Herren-Freitags-Zusatzaufgaben 6.5.05