9 Atomaufbau und Periodensystem

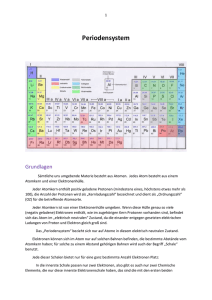
5. Atomaufbau und Periodensystem der Elemente
5.1 Historie: 1869 Meyer&Mendeleev: Konstruktion des Periodensystems
aus der Periodizität chemischer und physikalischer Eigenschaften
 Wertigkeit der Ionen
 formale Wertigkeit von Atomen in Verbindungen
 Reaktives Verhalten
 Atomvolumen
 Ionisierungsenergien
 Anordnung der
Elektronen in
Schalen
Besondere Stabilität der Edelgase
Sehr niedrige Ionisierungsenergien der
Alkalimetalle
5. Atomaufbau und Periodensystem der Elemente
Ionisierungsenergien:
• Besondere Stabilität der Edelgase
• sehr niedrige 1. Ionisierungsenergien der Alkalimetalle
• 2 Ionisierungsenergie: maximal für Alkalimetalle
minimal für Erdalkalimetalle
• Alkalimetalle – einwertig; Erdalkalimetalle - zweiwertig
 Aufbau neuer
Schalen mit
Alkalimetallen
Ab 1920: Erklärung des Atomaufbaus und des Periodensystems
aus der Quantenmechanik
Spektren  Aufbau von Mehrelektronen-Atomen
Optische Spektren  locker gebundene Elektronen
(Valenzelektronen)
Röntgen-Spektren  fest gebundene Elektronen
(Rumpfelektronen)
5. Atomaufbau und Periodensystem der Elemente
5.2 Wasserstoffähnliche Atome
 Einelektronen-Atome
 Alkali-Metalle

2
3
5.2.1 Einelektronen-Atome: H, He , Li , Be , 
 Einführung der Kernladung in E pot
Ze 2
 V(r) 
4 0 r
1
 Lösen der SGL analog zu H-Atom
e e 4 Z2 1
E n (Z)   2 2 2
8 0 h n
Einführung von Z in Wellenfunktion,
z.B. Grundzustand 1s:
s  const  e  Z
5. Atomaufbau und Periodensystem der Elemente
 Elektronenwolke näher am Kern lokalisiert, da
stärkere Anziehung durch höhere Kernladung
 rH  rHe  rLi2 
 Spektrallinien zu höheren Wellenzahlen verschoben,
aber Spektren qualitativ analog zum Spektrum des H-Atoms
5.2.2 Alkali-Metalle:
Optische Spektren durch äußeres Elektron (s-Elektron)
bestimmt  „Leuchtelektron“
Innere Elektronen schirmen Kernladung ab  Z  Zeff
Innere Elektronen + Atomkern = Atomrumpf
Z
Komplikation: Zeff kann nicht als Punktladung am Ort des Kerns
beschrieben werden
5. Atomaufbau und Periodensystem der Elemente
 Kugelsymmetrie der potentiellen Energie geht verloren
E n  f ()  n2-fache Entartung der Energieniveaus
wird aufgehoben
5.3 Mehrelektronen-Atome – generelle QM-Beschreibung
Einfachstes Beispiel: Helium - Z  2, 2e 
2

r12
1


r2 + r1
Hamilton-Operator:
2
2
2
2

1
2e
1
2e
1
e
2
2
ˆ 
1   2  


H

2 e
4 0 r12
4 0 r1
4 0 r2
Anziehung
Kern – Elektron 1
2
2
2
  2  2  2 ; i  1, 2
x i yi z i
2
i
Anziehung
Kern – Elektron 2
Elektron-ElektronAbstoßung
5. Atomaufbau und Periodensystem der Elemente
2
e
ˆ H
ˆ H
ˆ 
H
;
1
2
4 0 r12
1
2
2

1
2e
ˆ 
H
 i2 
i
2 e
4 0 ri
Ohne Elektron-Elektron-WW: Hamiltonoperator = Summe von 1e 
Hamiltonoperatoren
ˆ H
ˆ H
ˆ
H
1
2
    (x1 , y1 , z1 )    (x 2 , y 2 , z 2 )
Lösung der SGL  Lösung des H-Atoms  Wasserstoff-Wellenfunktionen
Elektron-Elektron-Abstoßung  Ĥ nicht separierbar
keine analytische Lösung der SGL möglich
 Näherungsverfahren erforderlich
5.4 Näherungsverfahren – Das Variationsprinzip
5.4 Näherungsverfahren
5.4.1 Das Variationsprinzip
Berechnung der Erwartungswerte der Energien des Atoms:
E 


 n Ĥ n d


 n  n d
ˆ  d
   n H
n
wenn  n normiert ist
  d       dx dy dz dx
1
1
1
2
 dx N dy N dz N
für N-Elektronen-System
 n = Eigenfunktion von Ĥ  E  E n
Berechnung von E
mit Testfunktion   E  
Man kann zeigen: wenn    n

E  En


 Ĥ d


  d
Variationsprinzip
5.4 Näherungsverfahren – Das Variationsprinzip
Anschaulich: das in der Natur realisierte System hat immer die niedrigste
Energie. Falsche Wellenfunktion  höhere Energie
 ist daher eine umso bessere Näherung für n, je niedriger
E  ist.
wenn E   E n     n ; wird aber in der
Regel nicht erreicht
 Beste Näherung wird durch Energiemininierung ermittelt:
 E

Ĥ d !



 Minimum

   d
 Energieminimierung durch Parametervariation:
  E 



c
i

c ji
0
mit   (c1 , c2 , , ck )
Näherungsverfahren zur Lösung der SGL
1. Variationsmethode
Berechnung des ErwartungsWerts der Energie mit Testfunktion    ( c1 , c2, , ck )
 Hˆ  d


   d
*
E
*
 En
Energieminimierung durch
Koeffizientenvariation
  E

 ci


 0

C j i
E  Minimum
 beste Approximation
von n
5.4.2 Hartree-Fock-Methode des selbstkonsistenten Feldes
Ansatz: Gesamtwellenfunktion = Produkt aus wasserstoffähnlichen
1-Elektronen-Wellenfunktionen
  g1 (r1 , 1 , 1 )  g 2 (r2 , 2 , 2 )  g N (rN , N , N )
i
wobei g i (ri , i , i )  h i (ri , Zeff ,i )  Y ,m (i , i )
Beschreibt Abschirmung des Elektrons i
durch „Feld“ der anderen Elektronen
Winkelanteil wird von Elektron-Elektron-WW
nicht beeinflusst
Möglicher Ansatz: h i (ri , Zeff ,i )  R n , (ri , Zeff ,i )
Iteratives Verfahren zur Bestimmung der Zeff ,i via Variationsprinzip:
1. Schritt: Variation von h1
  E

 Zeff ,1


 Zeff , j1
 0    g1 (r1 ,1 , 1 )  g 2 (r2 ,2 , 2 ) g N (rN ,N , N )
5.4.2 Hartree-Fock-Methode des selbstkonsistenten Feldes
2. Schritt: Variation von h2
  E

 Zeff ,2


 Zeff , j2
 0    g1 (r1 ,1 , 1 )  g2 (r2 ,2 , 2 ) g N (rN ,N , N )
Iterative Energieminimierung durch sukkzessive Optimierung aller Zeff ,i
Abbruch wenn
E 
*

 Ĥ d
   d
*
 konstant ,
d.h. wenn
E n ' 1  E n '   ;   sehr kleine Zahl, z.B. 104
 Zeff ,i  Z   i
5.4.2 Hartree-Fock-Methode des selbstkonsistenten Feldes
 Zeff ,i  Z   i
Zeff ,i = effektive Kernladung für Elektron i
Z
= Kernladung
i
= Slater-Abschirmkostante des Elektrons i
Bsp. Ermittlung von  für ein Außenelektron (4s) von Ca:
Energietermschema von Mehrelektronenatomen
Zahl und Art der Orbitale wie bei H-Atom;
Aber: Aufhebung der Entartung
Ursache: unterschiedliche Abschirmung von
s-, p- und d-Orbitalen
2s
größere AufenthaltsWahrscheinlichkeit am
Kernort  geringere
Abschirmung
niedrigere Energie
2pz
Knotenebene am
Kernort  stärkere
Abschirmung
höhere Energie
Aufbau des Periodensystems
Aufbauprinzip: 1) Energieniveau-Schema
2) Pauli-Verbot
3) Hundsche Regel
Nomenklatur:
H 1s1
He 1s2
Ne 1s22s22p6
Na [Ne]3s1