Elektrische Leitfähigkeit

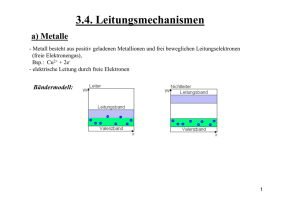
TU Ilmenau
Fakultät für Elektrotechnik und Informationstechnik
Institut für Werkstofftechnik
Ausgabe: September 2015
Dr. Tipp/Prof. Sp
Elektrische Leitfähigkeit (WSW)
(ElLeitW)
1 Versuchsziel
Kennenlernen des zerstörungsfreien Tastspul-Wirbelstromverfahrens zur Ermittlung der elektrischen Leitfähigkeit κ und daraus ableitbarer Eigenschaften von Metallen und Legierungen.
Kennenlernen der Vierspitzenmessmethode zum Bestimmen des Flächenwiderstandes RF bzw. des
spezifischen elektrischen Widerstandes ρ in Halbleitern und in dünnen metallischen Schichten.
2 Versuchsgrundlagen zur Leitfähigkeit
Je nach Charakters der Elektronen als Teilchen oder als Welle können zur Beschreibung der elektrischen Leitfähigkeit zum einen das anschauliche Elektronengas-Modell (Teilchenmodell) und zum
anderen die die Quanteneffekte berücksichtigende Bandstruktur verwendet werden, Bild 1a.
reales Bändermodell
vereinfachtes Bändermodell
k
Energie
Leitungsband
Leitungsbandunterkante
Valenzbandoberkante
EC
EG
EC
EG
EV
EV
Valenzband
richtungsabhängig
richtungsunabhängig
Bild 1: a) Bandstruktur eines indirekten Halbleiters (wie z. B. Siliziums) b) vereinfachtes Bändermodell bei T = 0 K, Valenzband vollständig gefüllt, Leitungsband leer [1]
Die Bandstruktur enthält die Abhängigkeit der Energie der Elektronen W vom Ausbreitungsvek→
−
tor K der Elektronenwelle unter Einbeziehung der Kristallstruktur und ist das Ergebnis umfangreicher Computerrechnungen. Das vereinfachte Energiebändermodell wird wie in Bild 1b gezeigt,
Kristallrichtungsunabhängig vereinfacht dargestellt.
Das Energiebändermodell (kurz Bändermodell) ist eine vereinfachte Beschreibung des Energiespektrums des Elektronenkollektivs im Festkörper. Für die elektrischen bzw. elektronischen Eigenschaften sind jeweils nur zwei Energiebänder maßgebend: Das höchstgelegene mit Elektronen
voll besetzte Band (Valenzband) und das darauf folgende nicht oder teilweise besetzte Band (Leitungsband), vgl. Bild 1b.
Für die quantitative Beschreibung der Leitungsvorgänge in metallischen Leitern wird überwiegend
das anschaulichere Elektronengas-Modell verwendet.
TU Ilmenau, Institut für Werkstofftechnik, FG Werkstoffe der Elektrotechnik
1
Versuch Elektrische Leitfähigkeit (ElLeitW)
2.1 Die elektrische Leitfähigkeit in massiven Metallen (Volumenmaterialien)
Metallische Leiterwerkstoffe dienen zum verlustarmen Transport von elektrischer Energie zwischen
Energieerzeugern und Energieverbrauchern oder zum Informationsaustausch zwischen den Bauelementen einer elektrischen Schaltung häufig in Form von Schaltkreisen. Sie zeichnen sich durch eine
hohe elektrische Leitfähigkeit aus, die vom Aufbau und weitestgehend vom Zustand des Materials
abhängig ist. Zu unterscheiden sind je nach Bindungsarten Ionen- und Elektronenleitung.
Bei den metallischen Leitern herrscht Elektronenleitung vor, die das Vorhandensein freier Elektronen voraussetzt. Die Valenzelektronen bilden mit 1022 . . . 1023 Elektronen/cm3 die Elektronenkonzentration n des Elektronengases [1].
Die Elektronenkonzentration n ändert sich mit der Temperatur von T = 0 K bis zur Schmelztemperatur nur unbedeutend.
Das Elektronengas umgibt die positiv geladenen Metallionen („Atomrümpfe “), die gesetzmäßig im
Raum angeordnet sind (Elektronengas-Modell). Infolge thermischer Wimmelbewegung (BROWNsche Bewegung) stoßen die Elektronen untereinander oder mit den Atomrümpfen elastisch zusammen. Die Strecke zwischen zwei Zusammenstößen nennt man „freie Weglänge“, sie beträgt etwa
10−1 nm. Unter Beachtung der Statistik wird für die weiteren Betrachtungen die „mittlere freie
Weglänge“ verwendet. Die Wahrscheinlichkeit für das Durchlaufen dieser Strecke ohne Stoß ist
W (x) = e−1 .
Die mittlere Geschwindigkeit dieser freien Elektronen beträgt ohne äußeres elektrisches Feld Null,
weil keine Bewegungsrichtung bevorzugt ist (Wimmelbewegung). Beim Anlegen eines elektrischen
Feldes E überlagert sich der ungerichteten thermischen Bewegung der Leitungselektronen eine
zusätzlich gerichtete Driftbewegung v. Die mittlere Driftgeschwindigkeit ist der elektrischen Feldstärke E proportional. Der Proportionalitätsfaktor zwischen v und E ist die Elektronenbeweglichkeit µ.
v =µ·E
(1)
Die Stromdichte j beträgt bei der Elektronenkonzentration n
j =e·n·v
(2)
j =e·n·µ·E
(3)
bzw. unter Verwendung von Gleichung (1)
Der Quotient aus Stromdichte j und Feldstärke E ist die spezifische elektrische Leitfähigkeit κ
j
=κ=e·n·µ
E
mit
µ=
e · lv
mef f · vF
(4)
(5)
wobei mef f die effektive Masse der Elektronen, vF die Elektronengeschwindigkeit und lv die mittlere freie Weglänge im Volumenmaterial sind.
Zur Charakterisierung von Stoffen im Hinblick auf ihre Verwendung als Leitermaterial für die
Elektrotechnik und Elektronik wird neben κ der spezifische elektrische Widerstand % verwendet.
Es gilt:
%=
1
κ
TU Ilmenau, Institut für Werkstofftechnik, FG Werkstoffe der Elektrotechnik
(6)
2
Versuch Elektrische Leitfähigkeit (ElLeitW)
Der elektrische Widerstand eines Metalls lässt sich aus der Streuung seiner Leitungselektronen an
den Störstellen des Kristalls und aus den temperaturabhängigen Gitterschwingungen (Phononen)
verstehen. Der spezifische elektrische Widerstand %v eines metallischen Leiters setzt sich dabei aus
zwei Anteilen zusammen (MATTHIESEN-Regel):
• einem temperaturunabhängigen spezifischen Restwiderstand %o (Störstellenanteil) und
• einem temperaturabhängigen Anteil %(T ) (Phononenanteil):
% = %o + %(T ) = %v = %volumen
(7)
Der temperaturunabhängige Restwiderstand %o ist folglich ein Maß für die Störstellenkonzentration
im Metall. Die Störstellen können dabei verschiedener Natur sein:
• Chemische Störstellen - Art und Anzahl der Fremdatome auf Gitter- oder Zwischengitterplätze (feste Lösungen);
• physikalische Kristallbaufehler wie Leerstellen, Versetzungen, Korngrenzen, Gitterverzerrungen . . ., die Streuzentren bilden [1].
Messtechnisch wird %o bestimmt bei tiefen Temperaturen.
Es gilt dann:
lim %(T ) = 0
T →0
(8)
Bei Temperaturen T > 0 K nimmt der Anteil %(T ) infolge der größer werdenden Ionenschwingungen immer mehr zu.
Wird Gleichung 7 grafisch dargestellt, zeigen die Kurven des spezifischen elektrischen Widerstandes
bei reinen Metallen in einem weiten Temperaturbereich (ca. 100 K bis 500 . . . 600 K) annähernd
lineares Verhalten [1].
Aufgrund der Linearität der %(T )-Kurven, die für viele Werkstoffe gilt, kann der spezifische elektrische Widerstand nach Gleichung 9 für unterschiedliche Temperaturen aus einem Bezugswert
berechnet werden:
%(T ) = %293K · (1 + α · ∆T )
(9)
wobei α der Temperaturkoeffizient bei 293 K und ∆T die Temperaturdifferenz (T − 293 K) sind.
Der Temperaturkoeffizient α gibt die prozentuale Änderung des spezifischen elektrischen Widerstandes bei einer von 293 K abweichenden Temperatur an.
Der spezifische elektrische Widerstand % ist mit der Wärmeleitfähigkeit des betreffenden Materials
durch das WIEDEMANN-FRANZ-LORENZsche Gesetz verknüpft, das besagt, dass das Verhältnis
von Wärmeleitfähigkeit λ und elektrischer Leitfähigkeit κ bei einer bestimmten Temperatur eine
Konstante ist.
λ
=γ·T
κ
(10)
γ = WIEDEMANN-FRANZ-LORENZsche Zahl = 2, 44 · 10−8 V 2 /K 2
Die Dimension von κ ist entweder MS/m oder % IACS (International Annealed Copper Standard).
Es gilt: 100 % IACS = 58 MS/m
Die Beschreibung der elektrischen Leitfähigkeit in metallischen Leitern mit dem Bändermodell
bedeutet einerseits, dass das Leitungsband nur zur Hälfte gefüllt ist oder andererseits, dass sich das
leere Leitungsband mit dem Valenzband überlappen. Die unbesetzten Energiezustände innerhalb
eines Bandes sind die Ursache für die elektrische Leitfähigkeit, denn nur in diesem Fall können
TU Ilmenau, Institut für Werkstofftechnik, FG Werkstoffe der Elektrotechnik
3
Versuch Elektrische Leitfähigkeit (ElLeitW)
die Elektronen beim Anlegen eines äußeren elektrischen Feldes Energie aufnehmen (entspricht auf
höhere Energieterme im Band gehoben werden) und sich zur positiven Elektrode bewegen, Bild 2.
Isolatoren
D E > 3(6) eV
Halbleiter
DE < 3(6) eV
einwertiges
Metall
zweiwertiges
Metall
E
r
Leitungsband
L
Leitungsband
Valenzband
L
Valenzband
VB
Valenzband
DE
Valenzband
Bild 2: Bändermodelle von Isolatoren, Halbleitern und Metallen [1]
2.2 Elektrische Leitfähigkeit in dünnen Metallschichten
Dünne metallische Schichten zeichnen sich gegenüber Volumenmaterialien durch eine höhere Fehlordnungsdichte aus, die insbesondere die mittlere freie Weglänge der Elektronen und damit den
spezifischen elektrischen Widerstand % stark beeinflussen. Eine weitere den elektrischen Widerstand dominant beeinflussende Größe ist die Schichtdicke d, da mit abnehmender Schichtdicke
immer mehr der zweidimensionale Charakter der Schicht dominiert und damit Oberflächenrauhigkeiten zunehmend die mittlere freie Weglänge und den spezifischen elektrischen Widerstand
beeinflussen, der bei dünnen Schichten keine Konstante mehr ist [2].
Für dünne Schichten muss deshalb Gleichung 7 um einen weiteren %-Term ergänzt werden, der
die Abhängigkeit des Oberflächeneinflusses berücksichtigt, so dass für dünne Schichten für den
spezifischen elektrischen Widerstand die Beziehung gilt:
% = %o + %(T ) + %(o) = %v + %(o)
(11)
%(o) berücksichtigt die diffuse Streuwirkung der Schichtoberfläche (Oberflächenrauhigkeit) und der
Grenzfläche zum Substrat auf die Bewegung der Elektronen.
Für den spezifischen elektrischen Widerstand %v , der die auf die freien Elektronen wirkenden
Streumechanismen im Volumen zusammenfasst, vgl. Gleichung 4 und Gleichung 5, gilt:
%v =
mef f · vF
%v =
e2 · n
mef f · vF 1
·
e2 · n
lv
1
lP h
1
1
1
+
+
+
+ ...
lS
lDef
lKG
(12)
!
(13)
Dabei ist zu berücksichtigen, dass die einzelnen Streumechanismen1 alle parallel wirken, so dass
die kleinste freie Weglänge den größten Einfluss auf % hat (parallel geschaltete Widerstände mit
je einem Streumechanismus).
1
lP h ist die mittlere freie Weglänge zwischen zwei Zusammenstößen Elektronen-Phonen. lS (Störstellen), lDef
(Gitterdefekte), lKG (Korngrenze)
TU Ilmenau, Institut für Werkstofftechnik, FG Werkstoffe der Elektrotechnik
4
Versuch Elektrische Leitfähigkeit (ElLeitW)
Die Berechnung der diffusen Streuwirkung der Oberfläche führte für dicke Schichten d/lv 1 zu
dem Ergebnis:
%(o) =
mef f · vF 3
·
e2 · n
8d
(14)
Die Summe von %v und %(o) ergibt den spezifischen elektrischen Widerstand %.
% = %v + %(o) =
mef f · vF 1
·
e2 · n
lv
% = %v
3lv
1+
8d
1+
3lv
8d
(15)
(16)
Bild 3a zeigt die Schichtdickenabhängigkeit des logarithmisch aufgetragenen spezifischen elektrischen Widerstandes %, während Teilbild 3b den der Dicke zuzuordnenden TK% wiedergibt.
Bild 3: Schichtdickenabhängigkeit elektrischer
Schichtparameter [1], a) spezifischer
elektrischer Widerstand %, b) Temperaturkoeffizient von %
Bild 4: Schichtbildungsstufen eines Goldfilmes
[2] Schichtdicke in nm: a) 1, b) 3, c) 10,
d) 20, e) 30, f) 20
Die Ursachen für den % = f(d)- und T K% = f (d)-Verlauf sind auf die unterschiedlichen Leitfähigkeitsmechanismen – Tunnelleitung und metallische Leitung – zurückzuführen, die durch die Schichtbildungsprozesse – Keimbildung, Inselschicht, Lückenschicht, geschlossene Schicht- einzeln oder
kombiniert auftreten, Bild 4.
Hergestellt werden derartig dünne Schichten mit Dickenbereichen von 10 . . . 1 000 nm hauptsächlich
durch Hochstromverdampfung, Elektronenstrahlverdampfung und durch Sputtern.
TU Ilmenau, Institut für Werkstofftechnik, FG Werkstoffe der Elektrotechnik
5
Versuch Elektrische Leitfähigkeit (ElLeitW)
2.3 Versuchsgrundlagen zur Leitfähigkeit im Halbleitern
Halbleiter sind Festkörper mit einem hohen spezifischen elektrischen Widerstand % und einen
negativen Temperaturkoeffizienten (T K% < 0). Wird die elektrische Leitfähigkeit von Ladungsträgern verursacht, die ausschließlich dem Halbleiterwerkstoff selbst entstammen, spricht man von
Eigenleitung und Eigenhalbleiter. Werden die Ladungsträger durch den Einbau von Fremdatomen
verursacht, spricht man von Störstellenleitung und Störstellenleiter. Im Unterschied zu Metallen
sind bei Eigenhalbleitern bei höchster Reinheit und Raumtemperatur 1012 . . . 1018 Elektronen/cm3
vorhanden. Das sind fünf bis elf Zehnerpotenzen weniger als bei Metallen.
Die auffälligsten Merkmale der Halbleiter sind die starke Abhängigkeit ihrer elektrischen Leitfähigkeit von der Temperatur und die gezielte Beeinflussung der elektrischen Leitfähigkeit durch den
kontrollierten Einbau von Fremdatomen in den Kristall (auf Gitterplätze) des reinen Halbleiters.
Hierbei werden im Silizium, einem der gebräuchlichsten Halbleiter, Si-Atome durch Atome der III.
Hauptgruppe (z. B. Bor) oder der V. Hauptgruppe (z. B. Phosphor) auf Gitterplätze substituiert.
Die überschüssige bzw. fehlende Ladung trägt, wenn das Atom auf einem Gitterplatz sitzt, zur
Leitung bei.
Die Elektronen aufnehmenden III-wertigen Elemente heißen Akzeptoren, die Elektronen spendenden V-wertigen Elemente heißen Donatoren. Die entstehenden Leitungsmechanismen werden
p- und n-Leitung genannt. Der Einbau der Fremdatome kann durch Diffusion, Dotierung oder
Ionenimplantation erfolgen [1].
Bild 5: Bändermodell eines a) n-Halbleiters und eines b) p-Halbleiters [1]
Zur Veranschaulichung allgemeiner Leitungsvorgänge wird auch hier das Elektronen- Teilchenmodell verwendet. Zur Darstellung von Potential-, Trägerdichte- und Strömungsverläufe - insbesondere bei der Beschreibung von pn-Übergängen, Metall-HL-Kontakten, Transistoren - erweist sich
das Bändermodell als vorteilhaft.
Im Unterschied zu den metallischen Leitern, wo entweder ein halbleeres Leitungsband existiert oder
sich Valenzband und Leitungsband überlappen, besteht bei den Halbleitern zwischen Valenzband
und Leitungsband ein für den Aufenthalt von freien Elektronen verbotener Energiebereich von
etwa < 3 eV (Si = 1,1 eV) - die verbotene Zone, vgl. Bild 2 und 5.
Handelt es sich um einen Störstellen-Halbleiter sind die Akzeptoren energiemäßig kurz oberhalb der
Valenzbandkante oder (nie und) die Donatoren kurz unterhalb der Leitbandkante in der verbotenen
Zone angeordnet, Bild 5.
Wird ein n-Halbleiter einer Temperaturskala ausgesetzt, Bild 6, wird sich bei tiefen Temperaturen
(T ∼ 0 K) ein hoher spezifischer elektrischer Widerstand % einstellen, weil keine freien Elektronen im Leitungsband vorhanden sind. Mit Temperaturzunahme bis T ∼ 100 K wird % infolge der
Störstellenleitung abnehmen, d. h. die elektrische Leitfähigkeit κ nimmt zu (a). Alle Störstellen
TU Ilmenau, Institut für Werkstofftechnik, FG Werkstoffe der Elektrotechnik
6
Versuch Elektrische Leitfähigkeit (ElLeitW)
(Donatoren) haben ihr Elektron ins Leitungsband an den Leitungsprozeß abgegeben (Störstellenerschöpfung). Eine weitere Temperaturzunahme führt zu einem κ-Abfall (b). Erreicht die Temperatur den Energiewert, dass Elektronen aus den Si-Bindungen den Leitungsprozeß bestimmen,
nimmt die spezifische elektrische Leitfähigkeit κ nochmal stark zu (c). Elektronen aus dem Valenzband überwinden die verbotene Zone und nehmen im Leitungsband am Leitungsprozeß teil
(Eigenleitung). In Bild 6 ist die κ = 1/% = f (1/T ) - Abhängigkeit gezeigt.
Bild 6: Elektrische Leitfähigkeit κ von n-Silizium als Funktion der Temperatur T
Bei den elektronischen Bauelementen wird nur die Störstellenleitung genutzt. Der Eigenleitungsmechanismus setzt bei Silizium etwa bei 125 o C ein, deshalb sind elektronische Bauelemente auf
Si-Basis nur bis zu dieser Temperatur einsetzbar.
Die elektrische Leitfähigkeit eines n-Halbleiters im Bereich der Störstellenleitung (Raumtemperatur) berechnet sich nach Gleichung
κ = e · n · µn
(17)
wobei die Elektronenkonzentration n bei Störstellenerschöpfung gleich der Donatorkonzentration ND ist (n = ND ). µn ist die Beweglichkeit der Elektronen. Wegen der einsetzenden Eigenleitung
und den entstehenden Elektronen-Loch-Paaren sind zusätzlich zu den bereits durch Dotierung entstandenen Elektronen - wenn auch in vergleichsweise sehr geringer Zahl - Löcher (p) vorhanden.
Wegen n p werden die Elektronen in einem n-Halbleiter als Majoritätsträger und die Löcher
als Minoritätsträger bezeichnet.
Beim p-Halbleiter sind wegen p n die Löcher die Majoritätsträger und die Elektronen die
Minoritätsträger.
Beim reinen Eigenhalbleiter setzt sich die Leitfähigkeit infolge der die Leitfähigkeit verursachenden
Elektronen-Loch-Paare aus zwei Summanden zusammen.
χ = e · (n · µn + p · µp )
(18)
wobei p die Löcherdichte und µp die Beweglichkeit der Löcher ist. Für einen Eigenhalbleiter gilt
n = p. Analog zum chemischen Massenwirkungsgesetz gilt in der Halbleitertechnik
n · p = ni 2 (T )
(19)
d. h. das Produkt aus Elektronen- und Löcherkonzentration ist bei vorgegebener Temperatur konstant. Diese Beziehung gilt auch für dotierte Halbleiter (Störstellenhalbleiter). ni ist die intrinsicDichte.
TU Ilmenau, Institut für Werkstofftechnik, FG Werkstoffe der Elektrotechnik
7
Versuch Elektrische Leitfähigkeit (ElLeitW)
3 Messung der spezifischen elektrischen Leitfähigkeit
3.1 Das Wirbelstromverfahren
Die Bestimmung des Absolutwertes der elektrischen Leitfähigkeit κ erfolgt im Labor üblicherweise
durch Strom-Spannungs-Messungen. Soll an einem Bauteil vor Ort die Leitfähigkeit ermittelt
werden, kommt u. a. das schnell und zerstörungsfrei messende Wirbelstromverfahren zum Einsatz.
Bild 7: Prinzip des Wirbelstrom-Leitfähigkeitssmessgerätes [3]
In Bild 7 ist der prinzipielle Aufbau eines Wirbelstrom-Leitfähigkeitsmessgerätes dargestellt. Bei
den Wirbelstromprüfverfahren wird je nach Anordnung der Prüfspulen noch einmal in solche
mit Durchlaufspule, mit Gabelspule und mit Tastspule unterschieden. Es handelt sich immer
um eine vergleichende Messmethode, bei der der am Bauteil erhaltene Messwert mit dem eines
Referenzstandards, dessen Leitfähigkeit bekannt ist, verglichen wird [2].
H
1
i
1
H
i
2
2
Probe
Bild 8: Wirkungsschema
des
Wirbelstromverfahrens [2]
Tastspul-
Bild 9: Komplexe Scheinwiderstandsebene der
Messsonde (Spule) [2] Po ohne Prüfteil,
P1 mit Prüfteil
Die auf den Messgegenstand aufzusetzende Sonde, wird wie in Bild 8 gezeigt, von einem Generator
mit einem Wechselstrom i1 einer bestimmten Frequenz gespeist. Durch das von der Erregerspule
erzeugte magnetische Wechselfeld H1 werden im Material Wirbelströme i2 induziert, deren Stärke
und Eindringtiefe auch von dessen elektrischer Leitfähigkeit abhängen. Die zur Erzeugung dieser
Ströme erforderliche Energie liefert das Magnetfeld, das dadurch mit größer werdenden Abstand
von der Oberfläche in seiner Intensität abnimmt. Das von Wirbelströme i2 nach der Lenzschen
Regel erzeugte Magnetfeld H2 überlagert sich dem Ursprungsfeld H1 .
Über die damit einhergehenden Änderungen der Messspuleneigenschaften wird das so entstehende
Magnetfeld erfasst [3, 4]. Die Spule besitzt ohne Prüfteil als sogenannten Leerwert einen ohmschen
oder Wirkwiderstand R, der vektoriell mit dem Blindwiderstand 2π · f · L = ω · L addiert, Bild 9,
TU Ilmenau, Institut für Werkstofftechnik, FG Werkstoffe der Elektrotechnik
8
Versuch Elektrische Leitfähigkeit (ElLeitW)
→
−
den Scheinwiderstand R ergibt. Befindet sich ein Prüfobjekt im Magnetfeld der Spule, kommt es
in ihm zur Wirbelstromausbildung, vgl. Bild 8. Dabei ändern sich die Spuleneigenschaften, speziell
→
−
der Wirk- und auch der Blindwiderstand.Der Endpunkt Po des Vektors R für den Leerwert wan→
−
dert nach dem Punkt P1 des neuen Vektors R 1 entsprechend der Differenz der Spulenparameter.
Der Scheinwiderstand wird so von seinem Absolutbetrag her und in seiner Phasenlage nach φ1
verschoben [3].
Die induzierte Spannung und der Übergang der Spulenparameter von Po nach P1 ist damit eine
Funktion
• der elektrische Leitfähigkeit κ des Messgegenstandes
• der relativen Permeabilität µr (wegen Beschränkung auf nichtferromagnetische Stoffe ist
µr = 1)
• der Probendicke d (Einfluss nur vorhanden, wenn Eindringtiefe des Magnetfeldes in der
Probe größer als Probendicke d)
• der flächenhaften Ausdehnung der Probe (bei Unterschreitung einer Mindestfläche)
• dem Abstand der Tastspule von der Probe
• der Messfrequenz f
• den geometrischen und elektrischen Eigenschaften der Prüfspule.
Demzufolge wird die Wirbelstommessmethode überall dort eingesetzt, wo es um die Bestimmung
jener Probeneigenschaften geht, die in einem Zusammenhang zu o. g. Einflussgrößen stehen oder
für die die elektrische Leitfähigkeit als Indikator für Änderungen der mechanischen Eigenschaften
dient:
•
•
•
•
•
•
•
•
•
•
Bestimmen der Härte von kaltaushärtbaren Leichtmetall-Legierungen
Bestimmen der Wärmeleitfähigkeit eines Metalls
Erkennen von Hitzeschäden bei Al-Legierungen (bei Flugzeugwartung)
Verwechselungsprüfung von Legierungen und Metallen
Reinheitsgradbestimmung an Metallen
Kontrolle der Homogenität an Metallen
Bestimmung der Aushärtung an Duraluminium
Schrottsortierung
Kontrolle von Festigkeit und Härte
Überwachung von Ausscheidungsvorgängen z. B. bei Cu-Cr-Legierungen
Die in der Praxis hauptsächlich verwendete Prüffrequenz liegt bei 60 kHz. In Abhängigkeit von
der Prüffrequenz ergibt sich damit eine Mindesteindringtiefe der Wirbelströme und indirekt eine
Mindesstärke des Messgegenstandes, Gleichung 20. Durch eine geeignete Wahl der Messfrequenz
kann die Probendicke variiert werden.
503
δ=√
f ·k
[mm]
(20)
f: Messfrequenz in Hz;
κ: elektr. Leitfähigkeit in m/(Ωmm2 );
γ: Eindringtiefe in mm
δkrit = 1, 7 · δ
(21)
δkrit : kritische Eindringtiefe, ab der sich die Dicke des Materials auf die Messergebnisse auswirkt.
TU Ilmenau, Institut für Werkstofftechnik, FG Werkstoffe der Elektrotechnik
9
Versuch Elektrische Leitfähigkeit (ElLeitW)
Neben der Dicke des Messgegenstandes können weitere Faktoren zu einer Verfälschung der Messwerte führen:
• der Sondenabstand zur Oberfläche
• die Größe der Messfläche (Randeffekte)
• die Krümmung der Messfläche.
Der Sondenabstand von der Messfläche wird bis zu 0,5 mm vom SIGMA-TEST-Gerät kompensiert, eventuelle Oberflächenkrümmungen und Randeffekte kann man durch Korrekturfaktoren
oder entsprechende Kalibrierungen berücksichtigen [5].
3.2 Vierspitzenmethoden [6, 7]
Zur %-Bestimmung werden bei Metallschichten (und Halbleiterscheiben) die Vierspitzenmethoden
mit unterschiedlicher Spitzenanordnung (linear oder quadratisch) eingesetzt. Voraussetzung für
kleine Messfehler ist, dass die Ausdehnung der Messprobe senkrecht und parallel zur Oberfläche als
groß gegen den Messspitzenabstand s angesehen werden kann (unendlich ausgedehnter Halbraum).
Dann kann das im Halbleiter bzw. Metallschicht entstehende elektrische Feld als Überlagerung
zweier kugelsymmetrische Potentialfelder aufgefaßt werden.
Da der spezifische elektrische Widerstand % dünner Metallschichten entsprechend Gleichung 16 keine Konstante ist, wird in der Dünnschichttechnik zur elektrischen Charakterisierung das Verhältnis
von %/d verwendet, das mit Flächenwiderstand RF (oder als Schichtwiderstand RS ) bezeichnet
wird:
%
RF =
[Ω]
(22)
d
Zur Bestimmung von RF werden die bereits genannten Vierspitzenmethoden und die Vierspitzenmethode nach Van der PAUW eingesetzt.
Bei bekannter Schichtdicke d kann dann aus Gleichung 22 der %-Wert bestimmt werden.
Bild 10: Messprinzip der Vierspitzenmessung [6], a) bei unendlicher Probendicke b) bei endlicher
Probendicke c) bei dünnen Schichten d) lineare und quadratische Viespitzenanordnung
TU Ilmenau, Institut für Werkstofftechnik, FG Werkstoffe der Elektrotechnik
10
Versuch Elektrische Leitfähigkeit (ElLeitW)
Das Messprinzip beruht meistens auf einer Gleichstrom-Spannungsmessung. Bei der Wahl des
Stromes ist darauf zu achten, dass keine Erwärmung der Schicht durch den Stromfluss auftritt, die
eine im Verhältnis zum massiven Metall große Änderung des spezifischen elektrischen Widerstandes
bewirken kann.
Weiterhin ist eine Mindestschichtdicke der zu messenden Schicht von 10 . . . 20 nm erforderlich,
damit die Schichten durch die ohnehin nur geringen Andruckkräfte der Spitzen von kleiner 20 mN
nicht durchstoßen werden.
Die Übergangswiderstände zwischen den Spitzen (des Messkopfes) und der Metallschicht werden
bei Verwendung einer Kompensationsschaltung oder eines hochohmigen Digitalvoltmeters zur Messung des Spannungsabfalles wirkungslos. Der Strom in der Größenordnung von 1 . . . 50 mA wird
mittels einer Konstantstromquelle mit einer maximalen Abweichung < 0,1 % in die Messprobe
eingespeist.
3.2.1 Die Vierspitzenmethode nach VALDES
Die Vierspitzenmethode wurde entwickelt zur Messung des spezifischen Widerstandes % an Halbleiter- Scheiben. Bei der theoretischen Begründung des Verfahrens geht man von punktförmigen
Stromquellen aus, die in einem unendlich ausgedehnten leitenden Medium mit örtlich konstanter
Leitfähigkeit angeordnet sind. Unendlich ausgedehnt bedeutet, dass die Ausdehnung des leitenden
Mediums senkrecht und parallel zur Oberfläche als groß gegen den Abstand der Stromquellen
voneinander angesehen werden kann.
Bei der linearen Vierspitzenmethode werden 4 Spitzen im gleichem Abstand s zueinander in einem Messkopf plaziert. Der Spitzenabstand s liegt im Bereich von 0, 5 ≤ s ≤ 1,5 mm. Erfolgt die
Stromeinspeisung, siehe Bild 10a, über die äußeren Spitzen und die stromlose Messung des Spannungsabfalles über die mittleren Spitzen und sind die Abmessungen der Messprobe groß gegen den
Spitzenabstand, berechnet sich der spezifische elektrische Widerstand % nach Gleichung 23.
% = 2π · s ·
U
I
(23)
Für endliche Fläche A und endliche Dicke d der Messprobe, Bild 10b, sowie unterschiedliche
Spitzenabstände werden Korrekturfaktoren KA , Kd und Ks eingeführt, die multiplikativ den geometrieabhängigen Korrekturfaktor K ergeben, so dass sich in diesem Fall % nach Gleichung (24)
berechnet:
U
(24)
% = 2π · s · · K
I
wobei K = KA · Kd · Ks ist.
Viele technische Anwendungen, insbesondere in der Mikroelektronik und Mikrosystemtechnik,
benötigen zur Funktionsweise der Bauelemente nicht mehr die Materialien als Volumenmaterialien
sondern als Schichtmaterialien, Bild 10c. Zur elektrischen Charakterisierung solcher HalbleiterDiffusionsschichten und Metallschichten wird der in Gleichung 22 definierte Flächenwiderstand RF
verwendet.
Liegt eine unendliche Schichtfläche und eine dünne zu messende Schicht mit der Schichtdicke d vor
und gilt weiterhin, dass der Spitzenabstand s d ist, dann kann für den Potentialverlauf um die
Stromspitzen ein zylindersymetrischer Feldverlauf angenommen werden. Durch Superposition der
Potentialverläufe erhält man für einen in der Mitte einer kreisförmigen Schicht vom Durchmesser D
aufgesetzten Vierspitzenmesskopf den Spannungsabfall:
TU Ilmenau, Institut für Werkstofftechnik, FG Werkstoffe der Elektrotechnik
11
Versuch Elektrische Leitfähigkeit (ElLeitW)
"
#
I ·%
(d/s)2 + 2)
I
1
U=
ln 2 + ln
= · RF ∗
2
π·d
(D/s) − 3)
π
K
(25)
wobei K ∗ wieder ein geometrieabhängiger Korrekturfaktor ist und für die verschiedenen d/s- und
D/s-Verhältnisse berechnet werden kann.
Für dünne Schichten (d s) und (D s) berechnet sich der Flächenwiderstand RF aus Gleichung
(26)
π U
RF =
·
(26)
ln 2 I
Außer der linearen Vierspitzenanordnung gibt es auch noch eine quadratische Vierspitzenanordnung, die bei gleichen Spitzenabstand zu einer größeren lokalen Auflösung führt, Bild 10d.
3.2.2 Vierspitzenmethode nach Van der PAUW
Bei dieser Methode werden die Spitzen 1 . . . 4 am Rand der zu messenden Probe aufgesetzt, Bild 11.
Ein Konstantstrom wird über die Spitzen 1 und 2 eingespeist; mit den Spitzen 3 und 4 wird der
Spannungsabfall stromlos gemessen → (R12,34 ).
Bild 11: Messprinzip der Van der PAUW Methode mit den vier Messspitzen 1, 2, 3, 4 am Probenrand, a) allgemeiner Fall, b) Probe mit Spiegelbildsymmetrie und symmetrisch angeordneten Kontakten
Danach wird der Strom ohne Änderungen der Spitzenkonfiguration über die Spitzen 2 und 3
eingespeist und der Spannungsabfall über die Spitzen 1 und 4 gemessen (→ R23,14 ). Nach Van
der PAUW verhalten sich die zwei experimentell ermittelten Widerstände R12,34 und R23,14 nach
Gleichung 27.
e
− π·d
·R12,34
%
+e
− π·d
·R23,14
%
=1
(27)
Der spezifische Widerstand % errechnet sich entsprechend Gleichung 28.
π · d (R12,34 + R23,14 )
·
·f
%=
ln 2
2
R12,34
R23,14
!
(28)
Für den Flächenwiderstand RF gilt:
π (R12,34 + R23,14 )
RF =
·
·f
ln 2
2
R12,34
R23,14
!
(29)
„f “ ist ein Korrekturfaktor, der nur vom Verhältnis R12,24 /R23,14 abhängt und folgende transzendente Gleichung 30 erfüllt:
"
#
(R12,34 )/(R23,14 ) − 1 ln 2
1
cosh
·
= · e(ln 2/f )
(R12,34 /(R23,14 ) + 1
f
2
TU Ilmenau, Institut für Werkstofftechnik, FG Werkstoffe der Elektrotechnik
(30)
12
Versuch Elektrische Leitfähigkeit (ElLeitW)
Bild 12: Abhängigkeit des Korrekturfaktors f vom Widerstandsverhaltens R12,34 /R23,14
Der Verlauf des Korrekturfaktors als Funktion von R12,34 /R23,14 ist in Bild 12 gezeigt.
Bei symmetrischer Probenanordnung und symmetrischer Spitzenordnung sind die gemessenen Widerstände gleich groß R12,34 = R23,14 = R.
Für % ergibt sich dann die Berechnungsgleichung:
%=
π·d
·R
ln 2
(31)
Der Vorteil dieser Methode liegt im geometrieunabhängigen Korrekturfaktor f. Der Korrekturfaktor
hängt nur vom Widerstandsverhältnis ab.
Bei dieser Methode wird ein integraler Widerstand über der gesamten Messprobe bestimmt. Inhomogenitäten im Flächenwiderstand, die auf Fehler der Technologie, z. B. beim Aufsputtern,
zurückzuführen sind, sind so nicht zu ermitteln.
3.2.3 Lineare Van der PAUW-Methode
Durch die Anwendung von verschiedenen Konfigurationen bei der Wahl der Stromeinspeisung bzw.
der entsprechenden Spannungsmessung konnte der Vorteil eines nur vom Widerstandsverhältnisses
abhängigen Korrekturfaktors der Van der PAUW-Methode mit der hohen örtlichen Auflösung der
linearen Vierspitzenmethode kombiniert werden.
Erfolgt eine Stromeinspeisung in drei verschiedenen Konfigurationen und die Spannungsmessung
entsprechend, dann verhalten sich die drei gemessenen Spannungen U43 , U23 und U24 entsprechend
Gleichung 32.
U23 = U24 + U43
(32)
Gleichung 32 kann gleichzeitig zur Überprüfung der Kontaktierung der Messprobe mit allen vier
Spitzen dienen.
Der Korrekturfaktor kann aus dem Verhältnis von zwei bestimmten Spannungsmessungen errechnet werden. Wenn V das Verhältnis der Spannungen ist,
V =
U23
R14,23
=
U43
R12,43
TU Ilmenau, Institut für Werkstofftechnik, FG Werkstoffe der Elektrotechnik
(33)
13
Versuch Elektrische Leitfähigkeit (ElLeitW)
ergibt sich aus Gleichung 30 die transzendente Gleichung:
V −1
1 lnf 2
f
= arccosh
·e
·
(34)
V +1
2
ln 2
Berechnet man f als Funktion von V, ergibt sich der Korrekturfaktor K ∗∗ zu Gleichung 35.
K
∗∗
π
1
=
1+
ln 2
V
· f (V )
(35)
Bild 13: Abhängigkeit des Korrekturfaktors K ∗∗ vom Spannungs- bzw. Widerstandsverhältnis V
Der Verlauf von K ∗∗ ist in Abhängigkeit vom Verhältnis V in Bild 13 dargestellt.
Der Flächenwiderstand berechnet sich nach Gleichung 36:
π
1
U
1+
· f (V ) ·
(36)
RF =
ln 2
V
I
Nachteilig bei diesem Verfahren ist, dass ein zyklisches Vertauschen von Stromeinspeisung und
Spannungsmessung an den Spitzen erfolgen muss. Dadurch verlängert sich die Messdauer auf die
3-fache Zeit.
4 Vorbereitungsaufgaben
1. Erklären Sie, weshalb elektrisch hochleitfähige Stoffe eine Metallbindung aufweisen, während
homöopolar gebundene Stoffe im allgemeinen gute Isolatoren sind!
2. Worin unterscheiden sich die Bändermodelle von Metall, Halbleiter und Isolator?
3. Warum gibt es bei Metallen Bändermodelle mit einem halbleeren Leitungsband und Bändermodelle wo sich Valenzband und Leitungsband überlappen?
4. Warum nimmt der spezifische elektrische Widerstand % bei Dünnschichtmaterialien mit abnehmender Schichtdicke zu?
5. Warum wird bei leitfähigen Dünnschichtmaterialien vornehmlich der Flächenwiderstand RF
gemessen, nach welchen Prinzip funktionieren die Messverfahren?
6. Berechnen Sie die kritische Eindringtiefe für Aluminium und Zinn für die Frequenzen 60 kHz,
120 kHz, 240 kHz und 480 kHz! Die Leitfähigkeitswerte der reinen Elemente sind der Literatur
zu entnehmen!
7. Erklären Sie über die Kornstruktur, warum die elektrische Leitfähigkeit so empfindlich auf
die Gefügeausbildung von Metallen reagiert!
TU Ilmenau, Institut für Werkstofftechnik, FG Werkstoffe der Elektrotechnik
14
Versuch Elektrische Leitfähigkeit (ElLeitW)
5 Praktikumsaufgaben
1. Inbetriebnahme des SIGMATEST D2.068 gemäß ausliegender Bedienungsanleitung!
2. Bestimmen Sie experimentell die Frequenzabhängigkeit der kritischen Eindringtiefe dkrit der
Wirbelströme für verschiedene Materialien und vergleichen Sie die Werte mit den theoretisch
errechneten aus Vorbereitungsaufgabe 4.
3. Weisen Sie experimentell den Zusammenhang zwischen Leitfähigkeit und dem linearen Kaltverformungsgrad anhand der ausliegenden Proben nach!
4. Es ist experimentell die Abhängigkeit des spezifischen elektrischen Widerstand % von der
prozentualen Zusammensetzung einer Nichteisen-Metall-Legierung (Zweistoffsystem) nachzuweisen und zu begründen.
5. Ermitteln Sie für die vorliegenden Proben die Wärmeleitfähigkeit λ und vergleichen Sie die
erhaltenen Werte mit den in der Literatur angegebenen Werten.
6. Für das in Aufgabe 5 gegebene Legierungssystem ist die Änderung der Wärmeleitfähigkeit λ
in Abhängigkeit vom Mischungsverhältnis der einzelnen Komponenten bei Raumtemperatur
nachzuweisen!
7. Für metallische Dünnschichtproben unterschiedlicher Dicke ist der Flächenwiderstand RF
nach der linearen van-der-PAUW-Methode zu ermitteln.
Eine detaillierte Aufgabenstellung liegt am jeweiligen Versuchsplatz im
Meitnerbau, G.-Kirchhoff-Str. 5, Raum 3.2.309 bzw. 3.2.306 aus!
Literaturliste
[1]
[2]
[3]
[4]
[5]
[6]
[7]
[8]
[9]
Nitzsche, K. ; Ullrich, H.-J.: Funktionswerkstoffe der Elektrotechnik und Elektronik. 2. Auflage. Leipzig.
Stuttgart : Hüthig Verlag, 1998. – 448 S. – ISBN 978–3778512647
Nitzsche, K.: Schichtmeßtechnik. 1. Auflage. Würzburg : Vogel Buch -Verlag, 1996. – 502 S. – ISBN
3–8083–1530–8
Neumaier, P. ; Materialprüfung, Sonderdruck (Hrsg.): Hochpräzise Messung der elektrischen Leitfähigkeit
von Nichteisen-Metallen nach dem Wirbelstromverfahren. Carl Hanser Verlag, liegt am Praktikumsplatz aus,
1990
Blumenauer, H.: Werkstoffprüfung. 6. korr. Auflage. Weinheim : VCH-Verlagsgesellschaft, 1994. – 426 S. –
ISBN 978–3342005476
Sigmatest D2.068 - Bedienungsanleitung, Firmenschrift Institut Dr. Förster. Reutlingen, liegt am Praktikumsplatz aus
Hadamovsky, H.-F.: Werkstoffe der Halbleitertechnik. 2. Auflage. Leipzig : Deutscher Verlag für Grundstoffindustrie, 1990. – 360 S. – ISBN 3–342–00315–4
Pfüller, S.: Halbleitermeßtechnik. Hüthig, 1977. – 284 S. – ISBN 978–3778503881
Macherauch, E. ; Zoch, H.-W.: Praktikum in Werkstoffkunde. 11. Auflage. Wiesbaden : Vieweg+Teubner
Verlag, 2011. – 602 S. – ISBN 978–3–8348–0343–6
Allgemeine Anforderungen an die Kompetenz von Prüf und Kalibrierlaboratorien; Deutsche und Englische
Fassung. In: Deutsche Norm DIN EN ISO/IEC 17025 Berichtigung 2:2007-05 (2007), S. 1–73
TU Ilmenau, Institut für Werkstofftechnik, FG Werkstoffe der Elektrotechnik
15