PowerPoint-Präsentation

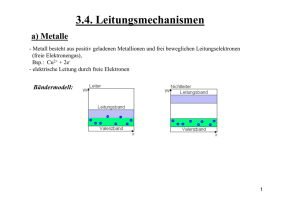
Elektrische und Thermische
Leitfähigkeit von Metallen
Virtueller Vortrag von Andreas Kautsch und Andreas Litschauer
im Rahmen der VO Festkörperphysik Grundlagen
Outline
 elektrische Leitfähigkeit
 Gründe für den elektrischen Widerstand
 Umklapp-Streuung
 Bewegung in Magnetfeldern – Hall Effekt
 Thermische Leitfähigkeit von Metallen
Elektrische und Thermische Leitfähigkeit von Metallen
2
2. Newtonsches Gesetz für ein freies Elektron



 1 
dv
dk
F m

  e( E  v  B )
dt
dt
c




F ... Kraft auf das Elektron
E ... elektrisches Feld
B ... magnetisches Feld
c ... Konstante im CGS-System
Elektrische und Thermische Leitfähigkeit von Metallen
3
Fermi-Kugel im elektrischen Feld
 das elektrische Feld E bewirkt im k-Raum eine Verschiebung der gesamten
Fermi-Kugel:

  eEt
k 

Elektrische und Thermische Leitfähigkeit von Metallen
4
Bewegung der Elektronen ohne äußeres Magnetfeld
 Driftgeschwindigkeit der Elektronen:

eE
v
m
 elektrische Stromdichte in einem konstanten E-Feld:


 ne E
j  nqv 
m
2
 wegen (Ohmsches Gesetz):


j  E
 ergibt sich die elektrische Leitfähigkeit zu:
ne 

m
2
Elektrische und Thermische Leitfähigkeit von Metallen
5
elektrische Leitfähigkeit am Beispiel Kupfer
 Leitfähigkeit von reinen Kupferkristallen bei 4 K fast 105 mal größer als
bei Raumtemperatur (283,15 K)
 daraus folgt für die mittlere freie Weglänge: l(4 K) ≈ 0,3 cm wohingegen
l(283,15 K) ≈ 3*10-6 cm
 maximal beobachtete mittlere freie Weglänge bei Temperaturen von
flüssigem Helium: 10 cm
Elektrische und Thermische Leitfähigkeit von Metallen
6
Experimente zum elektrischer Widerstand von Metallen
bei der Temperatur von fl. He (4 K) Stöße der Leitungselektronen mit
Verunreinigungen bzw. mechanischen Gitterfehler
-
Korngrenzen und Versetzungen
Fremdatome
Leerstellen
Zwischengitteratome
Konzentrationsschwankungen
Isotopenschwankungen
bei höheren Temperaturen (Zimmertemperatur) Stöße der Leitungselektronen mit
Gitterphononen
- im Bild rechts sind die Phononen durch
unterschiedliche Abstände der Netzebenen
symbolisiert
Elektrische und Thermische Leitfähigkeit von Metallen
7
Relaxationszeit
 bei Abschaltung von E geht Impulsverteilung
wieder in Grundzustand zurück nach:
 τL ... Stoßzeit mit Phononen
 τi ... Stoßzeit mit Gitterfehlern
1


1
L

1
i
 daraus resultiert der Widerstand im Metall
 ρL ... spezifischer Widerstand durch thermische
Phononen
 ρi ... spezifischer Widerstand durch Streuung der
Elektronenwellen an statischen Defekten
   L  i
Elektrische und Thermische Leitfähigkeit von Metallen
8
Matthiessensche Regel
 Matthiessensche Regel:
ρ(T) = ρPhononen(T) + ρDefekte
 wenn die Temperatur bzw. die
Konzentration der Defekte klein ist,
können die spezifischen Widerstände
unabhängig von diesen sein
 ρi(0) ist der auf 0 K extrapolierte
spezifische Widerstand;
ρL verschwindet mit T0
 Gitterwiderstand
ρL(T) = ρ - ρi(0)
ist derselbe für verschiede Proben aus
dem gleichen Metall
 Widerstandsverhältnis=
ρ(293,15)/ ρ(0)Maß für Reinheit
Elektrische und Thermische Leitfähigkeit von Metallen
9
Debyetemperatur
 Die Kollisionsrate von Elektronen mit Phononen ist proportional zur
Konzentration d. thermischen Phononen
 Über der Debyetemperatur Θ ist die Phonoenkonzentration proportional
zur Temperatur  ρ ~ T für T > Θ
 Beispiele für Debyetemperaturen in K:
Cs
Pb
NaCl
Cu
38
105
321
343
Al
Fe
C
428
467
2230
Elektrische und Thermische Leitfähigkeit von Metallen
10
Umklapp-Streuung (Stöße an Phononen)
 bei niedrigen Temperaturen: Änderung des Elektronenimpulses viel größer als
bei normaler Elektron-Phonon Streuprozess bei dieser Temperatur
 Erklärung: reziproker Gittervektor beteiligt
Normalprozess
(Kleinwinkelstreuung)
Umklapp-Prozess
(starke Streuzentren)
k‘ = k + q
k‘ = k + q + G
k: Elektronenimpuls vor Stoß; k‘: Elektronenimpuls nach Stoß
q: Phononenimpuls; G: reziproker Gittervektor
Elektrische und Thermische Leitfähigkeit von Metallen
11
Ergebnis von Bloch
 analytisches Ergebnis für die normale
Streuung bei sehr tiefen
Temperaturen:
L 
T
5

6
 konnte noch nicht nachgewiesen
werden, weil zu viele konkurrierende
Effekte wie:
- Störstellenstreuung
- Elektron-Elektron-Streuung
- Umklapp-Streuung
Elektrische und Thermische Leitfähigkeit von Metallen
12
Bewegung in Magnetfeldern
Elektrische und Thermische Leitfähigkeit von Metallen
13
Lorentzkraft auf ein Elektron in einem homogenen Magnetfeld B
 Im CGS-System:
 Im SI-System:
Elektrische und Thermische Leitfähigkeit von Metallen
14
Hall-Effekt
Das Hall-Feld:
 elektrisches Feld in Richtung j x B
 Strom j senkrecht zu Magnetfeld B
 Größe der Spannung:
 wobei
als Hall-Konstante bezeichnet wird und d die Dicke der
Probe parallel zu B ist
Elektrische und Thermische Leitfähigkeit von Metallen
15
Hall-Konstante

 ne E
j
m
2
 Mit
die Hallkonstante
und
eB
Ey  
Ex
m
erhalten wir für
1
RH  
ne
 Dieser Ausdruck ist negativ für freie Elektronen, denn e ist laut Definition positiv
 Ladungsträgerkonzentration klein => Betrag der Hall-Konstante groß
Elektrische und Thermische Leitfähigkeit von Metallen
16
Standardgeometrie für den Hall-Effekt
 Ein stabförmiger Körper mit rechteckigem Querschnitt wird in ein Magnetfeld B
gebracht
Elektrische und Thermische Leitfähigkeit von Metallen
17
 Ein elektrisches Feld E an die Elektroden angelegt, verursacht eine Stromdichte
j in Stabrichtung
 Ablenkung in y-Richtung von Magnetfeld erzeugt
 Schnitt senkrecht zur z-Achse, Driftgeschwindigkeit der Elektronen setzt gerade
ein
Elektrische und Thermische Leitfähigkeit von Metallen
18
 Elektronen auf der einen, positiver Ionen-Überschuss auf der anderen Seite
bis das Hallfeld (transversale elektrische Feld) die Lorentz-Kraft durch das
Magnetfeld gerade aufhebt
 Schnitt senkrecht zur z-Achse, Driftgeschwindigkeit im stationären Zustand
Elektrische und Thermische Leitfähigkeit von Metallen
19
 Tabelle: Vergleich zw. beobachteten Werten und direkt aus der Konzentration
der Ladungsträger berechneten Werten der Hall-Konstante
Elektrische und Thermische Leitfähigkeit von Metallen
20
Thermische Leitfähigkeit von Metallen
Elektrische und Thermische Leitfähigkeit von Metallen
21
Wärmeleitzahl K
 Vermögen des Stoffes, thermische Energie zu transportieren:
 Wärmeleitzahl
 v ... Teilchengeschwindigkeit
 C ... spezifischen Wärme pro Volumeneinheit
 l ... mittlere freie Weglänge
Elektrische und Thermische Leitfähigkeit von Metallen
22
Wärmeleitfähigkeit von Cu
 In unten stehendem Graph ist die Wärmeleitfähigkeit von Kupfer nach Berman und
MacDonald zu sehen
Elektrische und Thermische Leitfähigkeit von Metallen
23
Verhältnis aus thermischer und elektrischer
Leitfähigkeit
Wiedemann-Franzsche Gesetz:
 Das Wiedemann-Franzsche Gesetz zeugt von der Tatsache, dass in
Metallen die Ladungsträger auch Träger von Wärmeenergie sind
 Für alle Metalle bei nicht zu tiefen Temperaturen ist das Verhältnis aus
thermischer Leitfähigkeit K und elektrischer Leitfähigkeit σ direkt proportional
zur Temperatur
K


  kB 
2
2
  T
3  e 
Elektrische und Thermische Leitfähigkeit von Metallen
24
Zusammenfassung
 das elektrische Feld bewirkt im k-Raum eine Verschiebung der gesamten
Fermi-Kugel


 Ohmsches Gesetz: j  E
ne 2
 elektrische Leitfähigkeit:  
m
 bei der Temperatur von fl. He (4 K) Stöße der Leitungselektronen mit
Verunreinigungen bzw. mechanische Gitterfehler
 bei höheren Temperaturen (Zimmertemperatur) Stöße der Leitungselektronen
mit Gitterphononen
 Matthiessensche Regel: ρ(T) = ρPhononen(T) + ρDefekte
 Umklapp-Streuung bei niedrigen Temperaturen: Änderung des
Elektronenimpulses viel größer als bei normaler Elektron-Phonon Streuprozess
bei dieser Temperatur
Elektrische und Thermische Leitfähigkeit von Metallen
25
Zusammenfassung
 Lorentzkraft auf ein Elektron in einem homogenen Magnetfeld B
 Hall Konstante:
 Wärmeleitzahl:

 1 
F   e( E  v  B )
c
Ey
1
RH 

j x Bz
ne
1
K  Cvl
3
 Wiedemann-Franzsche Gesetz: in Metallen Ladungsträger auch Träger
von Wärmeenergie
Elektrische und Thermische Leitfähigkeit von Metallen
26
Wir bedanken uns fürs Zuhören!
Elektrische und Thermische Leitfähigkeit von Metallen
27