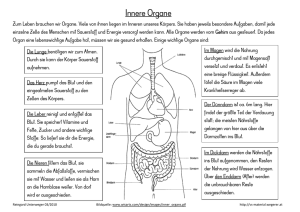
Blatt 04

Juniorprof. Dr. F. Lindner
Dr. M. Hefter & C. Vonwirth
Übungsblatt 4
TU Kaiserslautern
17.05.2016
Statistik II für Wirtschaftswissenschaftler SoSe 16
Abgabe: 20.05.2016 bis 13:45 Uhr
Aufgabe 1
Bei einer Bluttransfusion besteht die Gefahr, dass der Empfänger sich mit Hepatitis ansteckt. Zum
Glück gibt es einen effektiven Test zur Überprüfung von Spenderblut, bei dem die Konzentration
mg
eines bestimmten Enzyms (SGPT) im Blut gemessen wird (in 100ml
). Personen, die Träger von
Hepatitiserregern sind, haben im Mittel ein höheres SGPT-Niveau im Blut.
Aus der Analyse umfangreichen Datenmaterials ist bekannt, dass der Logarithmus der SGTPKonzentration etwa normalverteilt ist mit
• Mittelwert µ = 1.55 und Standardabweichung σ = 0.13 für, mit Hepatitiserregern, verseuchtes
Blut.
• Mittelwert µ0 = 1.25 und Standardabweichung σ0 = 0.12 für hepatitisfreies Blut.
Bevor Spenderblut in eine Blutbank aufgenommen wird, wird die SGPT-Konzentration gemessen.
Liegt diese unterhalb einer Schranke cα , so wird das Blut als erregerfrei akzeptiert.
a) Bestimmen Sie cα so, dass die Wahrscheinlichkeit für die Akzeptanz verseuchten Blutes genau
α ist für die Werte α = 0.01/α = 0.05/α = 0.10.
Hinweis: ln(cα ) ist α-Quantil einer Normalverteilung.
b) Berechnen Sie für jedes cα , α = 0.01/0.05/0.10, aus a) die Wahrscheinlichkeit, dass erregerfreies
Blut fälschlicherweise abgelehnt wird, d.h. dass die SGPT-Konzentration größer als cα ist.
Aufgabe 2
Sei X ∼ N (0, 1) standardnormalverteilt.
a) Sind X und −X identisch verteilt, d.h. haben X und −X die gleiche Verteilungsfunktion?
b) Sind X und X 2 identisch verteilt?
c) Sind X und −X unabhängig?
Aufgabe 3
Der Mittelwert µ einer Normalverteilung mit der Varianz σ 2 = 9 soll geschätzt werden. Eine Stichprobe vom Umfang N = 100 ergibt den Mittelwert 53.97.
a) Geben Sie ein 95%-Konfidenzintervall für µ an.
b) Wie groß müsste der Stichprobenmittelwert sein, damit das 95%-Konfidenzintervall höchstens
die Länge 0.4 hat?
c) Wie groß müsste der Stichprobenumfang sein, damit das 95%-Konfidenzintervall höchstens die
Länge 0.4 hat?
d) Geben Sie ein 99%-Konfidenzintervall für µ an.
Wie groß müsste nun der Stichprobenumfang sein, damit das 99%-Konfidenzintervall höchstens
die Länge 0.4 hat?
1/2
Juniorprof. Dr. F. Lindner
Dr. M. Hefter & C. Vonwirth
TU Kaiserslautern
17.05.2016
Übungsblatt 4
Aufgabe 4
Eine Stichprobe vom Umfang N = 12 ergibt folgende Füllmengen für Zementsäcke:
434.5072
443.3939
445.3890
445.3756
457.5347
435.8685
449.2864
434.8056
454.5647
457.3122
436.3218
448.1124
Die Varianz σ 2 = 10 der zur Befüllung genutzten Maschine sei bekannt.
a) Wählen Sie ein geeignetes statistisches Modell.
b) Bestimmen Sie ein 95%-Konfidenzintervall für die mittlere Füllmenge µ.
Falls Sie sich dazu entschließen Lösungen zu diesem Übungsblatt einzureichen, so werfen Sie diese bitte in den „Briefkasten“ ihres Übungsleiters.
Die Briefkästen befinden sich im Erdgeschoss von Gebäude 48.
2/2