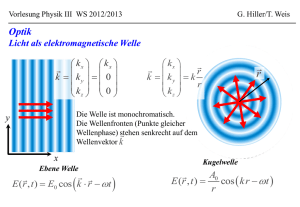
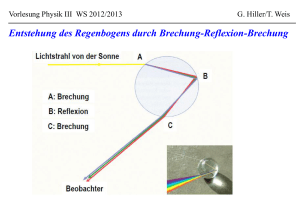
Kein Folientitel - Delta
Werbung

Vorlesung Physik III WS 2012/2013 Kreiselphysik Kreisel sind starre Körper mit hoher Symmetrie, die bei Rotation um diese Symmetrieachsen sehr stabil laufen können. Lagert man den Kreisel so, dass keine Drehmomente M auf ihn wirken, so bleibt wegen G. Hiller/T. Weis L, dL M 0 dt der Drehimpuls L räumlich konstant. Bei Rotation um die Hauptträgheitsache sind dann Figurenachse, Drehachse und Richtung von L parallel, sowie räumlich und zeitlich konstant. Kreisel nach Magnus (mit kardanischer Aufhängung): freie Bewegung in 3D und drehmomentfrei ! Vorlesung Physik III WS 2012/2013 G. Hiller/T. Weis Experiment Kurskreisel: Ein solcher kräftefreier Kreisel behält seine einmal vorgegebene Orientierung (roter Pfeil) auch dann bei, wenn man ihn mit dem Aufbau als Ganzes beliebig durch den Raum trägt. Ein Kreisel kann so im Prinzip als Kurskreisel zur Richtungsbestimmung in der Navigation eingesetzt werden. In der Praxis geschieht dies kaum, da geringste Reibungseffekte und Drehmomente die Orientierung langsam ändern. Stattdessen nutzt man Kreiselkompasse, die allerdings der Corioliskraft aufgrund der Erddrehung bedürfen! (siehe unten) L, Magnus-Kreisel als Kurskreisel Vorlesung Physik III WS 2012/2013 G. Hiller/T. Weis Stabilität von Kreiseln: Drehung um die Zylinderachse = Symmetrieachse. Die Rotation ist stabil, die Kraft auf die Achse ist zeitlich konstant. Drehung um eine Achse, die nicht Symmetrieachse ist. Bei Rotation wirken zeitlich veränderliche Kräfte auf die Achse (Schleudermomente, „Unwucht“). Vorlesung Physik III WS 2012/2013 G. Hiller/T. Weis Stabilität von Kreiseln: Experiment: „Backstein-Rotation“ Rotationen sind nur um bestimmte Achsen stabil. Diese Achsen heißen Hauptträgheitsachsen und fallen bei symmetrischen Körpern mit den Symmetrieachsen zusammen. Aber auch Körper ohne jede Symmetrie haben 3 Hauptträgheitsachsen. Bei Rotation um eine Trägheitsachse ist aber nur die Rotation um die Achsen mit dem kleinsten und größten Trägheitsmoment stabil. Geringste Abweichungen der Anfangsbedingungen von der Rotation um die Hauptachse mit mittleren Trägheitsmoment führt zum exponentiellen Anwachsen der Störung. Dies ist eine direkte Folge der Lösung der EulerGleichungen. Vorlesung Physik III WS 2012/2013 G. Hiller/T. Weis Nutation von Kreiseln: Rotiert der kräftefreie Kreisel nicht um eine Symmetrieachse, so bleibt nur die Richtung des Drehimpulses konstant. Allgemeiner Zusammenhang zwischen Drehimpuls und Winkelgeschwindigkeit: (t ) L const. S. Achse(t ) ˆ L J Vektor L zeigt nicht mehr in Richtung von . Das Trägheitsmoment I (bisher ein Skalar) wird dann zum Tensor! Nutation des kräftefreien Magnuskreisels Drehachse und Symmetrieachse des Kreisels ändern mit der Zeit ihre Richtung und bewegen sich auf „Kegelmänteln“ um die Richtung des ortsfesten Drehimpulses Vorlesung Physik III WS 2012/2013 möglicher Kreisel Ia Ib c symmetrischer Kreisel Kreiseltypen und Hauptachsen G. Hiller/T. Weis Ia Ic Ia Ic bei Rotation um Hauptachse zeigt immer in Richtung von L Ia Ic Trägheitsellipsoid c Vorlesung Physik III WS 2012/2013 G. Hiller/T. Weis Ia Ib Nutation des kräftefreien Kreisels bei Rotation um nicht Hauptträgheitsachse zeigt nicht in Richtung von L Es gilt die Erhaltung des Drehimpulses L . Der Vektor und die Figurenachse laufen auf Kegelmänteln um L . Zu sehen ist allerdings nur die Bewegung der Figurenachse. Ia Ic Ia Ic Ia Ic Vorlesung Physik III WS 2012/2013 G. Hiller/T. Weis Nutation der Erde: c<a Die Erde ist ein leicht abgeplattetes Rotationsellipsoid und damit kein idealer Kugelkreisel: a = b = 6378 km (Äquator) c = 6357 km (zum Pol) a 1 1 1 mErde b 2 c 2 , I b mErde a 2 c 2 , I c mErde a 2 b 2 5 5 5 Es ist a b c aber a c, so dass a c 2a und a c a Ia Ia Ic a2 c2 (a c)(a c) c 2 2 c c Ia b c a2 c2 2a a a 21 km 2 2 c c 2a 2 a 6378 km 1 Tag 304 Tage Nutationsperiode : T 304 Tage Chandler - Periode (gemessen) : T 433 Tage Die Erdachse bewegt sich innerhalb eines Kreises von 10 m Durchmesser. Vorlesung Physik III WS 2012/2013 Kreiselkompass G. Hiller/T. Weis kräftefreie Kurskreisel (Drehimpulserhaltung) zur Navigation nicht geeignet, da Antrieb notwendig und somit immer Drehmomente, wenn auch nur kleine, zur Abweichung führen ! Kreiselkompass mit permanentem Antrieb; Corioliskraft führt zur Ausrichtung parallel zur Drehachse des Koordinatensystems Vorlesung Physik III WS 2012/2013 G. Hiller/T. Weis Erde,Stuhl FCoriolis 2m Erde v Kreisel F v Fc v Kräftepaar entspricht Drehmoment, das die Drehachse des Kreisels in die Richtung der Drehachse der Erde zwingt. Dort verschwindet das Drehmoment. Kreisel ist in der dazu senkrechten Bewegungsrichtung gefesselt (Federn) Vorlesung Physik III WS 2012/2013 G. Hiller/T. Weis Eulersche Kreiselgleichungen: I aa I c I b bc M a I bb I a I c ca M b I cc I b I a ab M c Drehung des asymmetrischen Kreisels um eine Achse, die nicht Hauptträgheitsachse ist, führt zu unübersichtlichem, nichtlinearem Verhalten. Deterministisches Chaos Dynamik hängt äußerst empfindlich von den Anfangsbedingungen ab. Euler 1765 nichtlineares und gekoppeltes System von Differentialgleichungen in den Komponenten von einfache Lösungen nur für ganz wenige Spezialfälle !