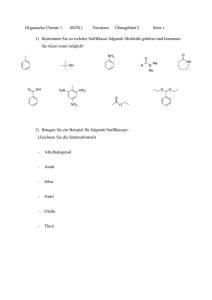
2 Die kinetische Gastheorie: Lernziele 2. Die kinetische Gastheorie

2 Die kinetische Gastheorie: Lernziele
2.
o
Einführung in das zugrundeliegende Modell des perfekten Gases
o
Der Druck eines perfekten Gases nach den kinetischen Gastheorie
o
Die Mittelwerte diskreter und kontinuierlicher Verteilungen
o
g der
Die Maxwell-Boltzmannsche und Maxwellsche Verteilung
Molekülgeschwindigkeiten
o
Berechnung der mittleren Geschwindigkeit, der quadratisch gemittelten
Geschwindigkeit und der wahrscheinlichsten Geschwindigkeit der Teilchen eines
Geschwindigkeit,
Gases
o
Stossquerschnitt, Stosszahl und mittlere freie Weglänge der Teilchen eines Gases
P. Atkins,
P
Atkins J.
J de Paula,
Paula “Physikalische
Physikalische Chemie
Chemie”, Wiley
WileyVCH Verlag GmbH& Co, 2010, 21.1
Die kinetische Gastheorie: Einleitung
o Die Energie eines Gases = kinetische Energie seiner Moleküle.
o Die
Gastheorie
=
mikroskopisches
Modell
zur
Berechnung
makroskopischer Eigenschaften
o Die
Di Gastheorie
G th i beruht
b ht auff drei
d i Annahmen:
A
h
1. Das Gas besteht aus Molekülen in kontinuierlicher, zufälliger Bewegung
2. Die Grösse der Moleküle : Strecke zwischen 2 Zusammenstössen
3. Es gibt keine Wechselwirkungen zwischen den Molekülen ausser
gelegentlichen kurzen, elastischen Stössen.
Kinetische Energie und Temperatur
o Die kinetische
Gasteilchens ist:
Energie
(für
Translationsbewegung)
1
2
ε trans = m v 2
oDer Druck des Gases ist:
pVm =
2
pVm = N Aε trans
3
1
N Am v 2
3
o Gasgesetz (ideale Gase): pVm = RT
N Aε trans =
eines
3
RT
2
3
2
ε trans = kT
Di Wä
Die
Wärme iistt eine
i A
Artt von B
Bewegung !
Wärme und mechanische Energie sind verwandt
Die quadratisch gemittelte Geschwindigkeit
o Die quadratisch gemittelte Geschwindigkeit der Gasmoleküle ist
proportional zur Wurzel aus der Temperatur und umgekehrt proportional
zur Wurzel aus der Molmasse:
v
2
3RT
=
M
c=
v
2
⎛ 3RT ⎞
=⎜
⎝ M ⎠
1
2
M = molare Masse
der Moleküle
An Tafel...
o Die einzelnen Geschwindigkeitswerte
g
sind über einen weiten Bereich
verteilt
o Die einzelnen Geschwindigkeitswerte werden zusätzlich durch ständige
Stossereignisse umverteilt:
ƒ vor einer Stoss kann sich ein Teilchen schnell bewegen
ƒ durch Stosseinwirkung kann das Teilchen auf seht hohe Geschwindigkeit
beschleunigt sein.
ƒ durch den nächsten Stoss kann das Teilchen wieder abgebremst werden.
M
Maxwell‘schen
ll‘ h Geschwindigkeitsverteilung
G
h i di k it
t il
o Wir brauchen die Verteilung der Komponenten der TeilchenGeschwindigkeiten zur Berechnung von Reaktionsgeschwindigkeiten
und zur Beschreibung der Eigenschaften von Molekularstrahlen.
o Der Anteil der Moleküle mit einer Geschwindigkeit zwischen v und v +
d ist
dv
i t zur Grösse
Gö
d betrachteten
des
b t ht t
B i h proportional
Bereiches
ti
l und
d wird
i d mit
it
F(v)dv bezeichnet.
o Wenn das gegebene Geschwindigkeits- Intervall so breit ist (v1 v2),
dann:
N = ∫ F (v )dv
v2
v1
o F(v) ist die Geschwindigkeitsverteilung, die für die Moleküle eines
Gases
bei
der
Temperatur
T
ist
die
Maxwell‘schen
Geschwindigkeitsverteilung:
3
2
M 2
⎛ M ⎞
2 − Mv
2 RT
F (v ) = 4 π ⎜
⎟ v e
⎝ 2 π RT ⎠
Maxwell‘schen Geschwindigkeitsverteilung
g
g
o Der Anteil der Moleküle mit einer Geschwindigkeit zwischen v1 und v2
ist das Fläche unter der Kurve zwischen v1 und v2.
N = ∫ F (v )dv
d
v2
v1
o Die Fläche unter der
Graphen von F(v) muss
numerisch
ausgerechnet
werden.
Re
elative Anza
ahl der Mole
eküle
Mittlere Geschwindigkeit
Moleküle
Moleküle
Moleküle
Geschwindigkeit
v1
v2
Maxwell‘schen
Maxwell
schen Geschwindigkeitsverteilung
Herleitung:
o Um die Wahrscheinlichkeit dass ein Molekül eine Geschwindigkeit im
Bereich von v bis v+dv besitzt, zu ermitteln, berechnen wir die
Wahrscheinlichkeit dafür, dass der Geschwindigkeitsvektor irgendwo auf
eine Kugel Fläche mit dem Radius v zeigt.
2
2
2
2
o Die Wahrscheinlichkeit dass
ein Molekül eine Geschwindigkeit
mit Komponenten
p
zwischen vx
und vx+dvx; vx und vy+dvy; vz und
vz+dvz hat, ist:
v = vx + v y + vz
Oberfläche
4πv2
Dicke
dv
v
F (v x , v y , v z )dv x dv y dv z
o Die Geschwindigkeitsverteilung
ist raumsymmetrisch:
vz
vx
F (v x , v y , v z )dv x dv y dv z = f (v x ) f (v y ) f (v y )dv x dv y dv z
vy
Maxwell‘schen Geschwindigkeitsverteilung
Herleitung:
o Boltzmann Verteilung = Der Anteil der Moleküle
Geschwindigkeitskomponenten vx, vy, vz, ist proportional
Exponentialfunktion ihrer kinetischen Energie E.
E=
1
1
1
mv x2 + mv y2 + mv z2
2
2
2
F (v x , v y , v z ) = Ae
F (vx , v y , vz ) = Ae
A
−E
kT
− mvx2
2 kT
mit den
zu einer
− mv2y
e 2kT e
− mvz2
2 kT
o Der Anteil der Moleküle mit den Geschwindigkeitskomponenten im
Geschwindigkeitsbereich vx und vx+dvx; vy und vy+dvy; vz und vz+dvz, ist:
−mvx2
−mv2y
−mvz2
F(vx , vy , vz )dv
d xdv
d y dv
d z = Ae
A 2kT e 2kT e 2kT dv
d xdv
d y dv
dz
F (v x , v y , v z )dv x dv y dv z = f (v x ) f (v y ) f (v y )dv x dv y dv z
f (v x ) = A 3 e
1
− mv x2
2 kT
− mv 2y
f (v y ) = A 3 e 2 kT
1
f (v z ) = A 3 e
1
− mv z2
2 kT
Maxwell‘schen Geschwindigkeitsverteilung
g
g
Herleitung:
o Zur Bestimmung von A überlegen wir, dass die Geschwindigkeit jedes
− ∞ < vx < + ∞
Moleküls irgendwo im Bereich
liegen
muss:
∞
∞
∫ f (v )dv
x
x
−∞
=1
⎛ m ⎞
A=⎜
⎟
2
π
kT
⎠
⎝
3
2
⎛ M ⎞
=⎜
⎟
2
π
RT
⎠
⎝
3
als
2
∫e
−∞
− ax
2
⎛π ⎞
dx = ⎜ ⎟
⎝a⎠
1
1
2
⎛ M ⎞
f (vx ) = ⎜
⎟ e
⎝ 2πRT ⎠
An Tafel...
2
−mvx2
2 kT
o Die Wahrscheinlichkeit dass ein Molekül eine Geschwindigkeit mit
Komponenten zwischen vx und vx+dvx; vx und vy+dvy; vz und vz+dvz hat,
ist:
2
3
− Mv
⎛ M ⎞ 2 2 RT
F (v x , v y , v z )dv x dv y dv z = ⎜
dv x dv y dv z
⎟ e
⎝ 2πRT ⎠
mit
v 2 = v x2 + v y2 + v z2
Maxwell‘schen
Maxwell
schen Geschwindigkeitsverteilung
Herleitung:
o Das Volumen der betreffenden Kugelschale=
g
die Summe aller
Volumenelemente:
dvx dv y dvz = 4πv 2 dv
Oberfläche
4πv2
vz
o Die Wahrscheinlichkeit, dass die
Geschwindigkeit unabhängig von
ihrer Richtung zwischen v und v+dv
+d
liegt:
3
⎛ M ⎞ 2 −Mv
F (v )dv = 4π ⎜
⎟ ve
⎝ 2πRT ⎠
2
Dicke dv
v
vx
2
2RT
dv
3
⎛ M ⎞ 2 2 − Mv 2 2 RT
F (v ) = 4π ⎜
v e
⎝ 2πRT ⎠
Maxwell‘schen Geschwindigkeitsverteilung
vy
Eigenschaften der Verteilung
o Der Anteil der Moleküle mit sehr hoher
Geschwindigkeit wird sehr gering sein.
o Schwerere
Moleküle
bewegen
wahrscheinlich nicht seht schnell.
100K
300K
sich
800K
o Bei höheren T bewegt
be egt sich ein grosser Teil der
Moleküle schneller als bei niedrigen T.
o Der Anteil von Molekülen mit sehr
geringer Geschwindigkeit ist klein
Mittlere Geschwindigkeit
Relative Anzahll der Moleküle
o Die Verteilung
g wird breiter bei höheren T
Moleküle
Moleküle
Geschwindigkeit
Moleküle
Geschwindigkeiten
g
der Moleküle
o Die mittlere Geschwindigkeit, v kann man aus der Maxwell-Verteilung
berechnen:
∞
v = v = ∫ vF (v )dv
−∞
⎛ 8 RT ⎞
v = v = ⎜
⎟
π
M
⎝
⎠
1
2
⎛ 8 kT ⎞
= ⎜
⎟
π
m
⎝
⎠
1
2
o Die wahrscheinlichste Geschwindigkeit,
g
, v* ergibt
g sich aus der Lage
g des
Maximus der Verteilung:
dF (v )
=0
dv
⎛ 2 RT ⎞
v∗ = ⎜
⎟
⎝ M ⎠
1
2
⎛ 2 kT ⎞
=⎜
⎟
⎝ m ⎠
1
2
o Die mittlere Relativgeschwindigkeit, vrel ist die mittlere Geschwindigkeit,
mit der ein Molekül sich einem anderen nähert:
vrel = 2v
Geschwindigkeiten der Moleküle
o Zusammenfassung der Schlussfolgerungen,
die sich aus der Maxwell-Verteilung für
Moleküle mit der Molmasse m und der
Temperatur T ergeben:
• die wahrscheinlichste Geschwindigkeit,
v∗ = c ∗
• die mittlere Geschwindigkeit,
v = v = c
• die quadratisch gemittelte Geschwindigkeit,
c=
v2
o Die mittlere Relativgeschwindigkeit zweier
verschiedener Moleküle:
mm
µ= 1 2
m1 + m2
vrel
⎛ 8kT ⎞
= ⎜⎜
⎟
⎝ πµ ⎠
Die Stosshäufigkeit
o Wir betrachten die Moleküle als harte
K
Kugeln
l (Durchmesser
(D h
d)
d).
o Die Moleküle „treffen“ sich, wenn der
Abstand der Mittelpunkte beider Teilchen ≤
St
Stossdurchmesser
d h
d
d.
o Die Positionen aller Moleküle, mit Ausnahme
von einem, sollen eingefroren sein.
o Um ein Teilchen (dies fliegt eine Zeit ∆t lang mit vrel) herum einsteht ein
Stosszylinder mit:
o Treffzahl der Moleküle = die Anzahl
ƒQuerschnitt σ = πd 2
ortsfester Moleküle deren Mittelpunkte sich
L = vrel ∆t
ƒLänge
innerhalb des Stosszylinder befinden:
V = σvrel ∆t
ƒVolumen
N
N ∗ = σ v rel ∆ t
V
Teilchendichte
Di Stosshäufigkeit
Die
St
hä fi k it
o Die Stosshäufigkeit Z = der Anzahl der Stösse eines Moleküls pro
Z it i h it mit
Zeiteinheit
it N Molekülen
M l kül in
i Volumen
V l
V
V,:
Z =
N
σ v rel
V
o Bei konstanten Volumen, Z nimmt mit der Temperatur zu.
o Bei konstanter Temperatur, Z ist proportional zum Druck t.
o Für ideale Gase:
Z = σ v rel
p
kT
o z. B. N2 Moleküle, p = 105 Pa, T = 25 °C > Z = 5x109 s-1
σ (nm2 )
0.88
0.21
0.43
Moleküle
Benzol
Helium
Stickstoff
Die mittlere freie Weglänge
o Die mittlere Weglänge, λ = die mittlere Wegstrecke, die ein Molekül
zwischen zwei Stössen zurücklegt.
o Ein Molekül verbringt zwischen Stössen eine freie Flugzeit 1/Z
bewegt sich um eine Strecke, l :
l =λ
und
v
λ=
Z
o Die mittlere freie Weglänge:
kT
λ=
2σ p
ƒQuerschnitt
σ = πd 2
o z.B. Stickstoff, p = 105 Pa (das bedeutet 103 Moleküldurchmessern) >
λ = 70nm.
o In einem geschlossenem Behälter, T/p = konst. >
λ ≠ f (T )
2 Die kinetische Gastheorie: Lernziele
2.
9 Einführung in das zugrundeliegende Modell des perfekten Gases
9 Der Druck eines perfekten Gases nach den kinetischen Gastheorie
9 Die Mittelwerte diskreter und kontinuierlicher Verteilungen
9 Die
Di Maxwellsche
M
ll h Verteilung
V t il
d Molekülgeschwindigkeiten
der
M l kül
h i di k it
9 Berechnung der mittleren Geschwindigkeit, der quadratisch gemittelten
Geschwindigkeit, und der wahrscheinlichsten Geschwindigkeit der Teilchen eines
Gases
9 Stossquerschnitt, Stosszahl und mittlere freie Weglänge der Teilchen eines Gases
P. Atkins,
P
Atkins J.
J de Paula,
Paula “Physikalische
Physikalische Chemie
Chemie”, Wiley
WileyVCH Verlag GmbH& Co, 2010, 21.1
Thermodynamik (TD)
Fundamentale Theorie der makroskopischen Eigenschaften der
Materie:
- Spontane Prozesse
- Konzept der “Temperatur”
-Phasenübergänge
-Energetik
Energetik makroskopischer Phasen und chemischer Reaktionen
P. Atkins,
P
Atkins J.
J de Paula,
Paula “Physikalische
Physikalische Chemie
Chemie”, Wiley
WileyVCH Verlag GmbH& Co, 2010.
Der erste Hauptsatz der TD- Lernziele
o Einleitung
o Zustandgrössen und –funktionen
o Wärme, Arbeit und Energie
o Innere Energie
o Der erste Hauptsatz der Thermodynamik
o Volumenarbeit
o Wärmeübergänge
o Die Enthalpie
o Adiabatiche Anderung
o Anderungen der Inneren Energie
o Der Joule-Thomson-Effeckt
ff
oThermochemie
P. Atkins,
P
Atkins J.
J de Paula,
Paula “Physikalische
Physikalische Chemie
Chemie”, Wiley
WileyVCH Verlag GmbH& Co, 2010, 2.
Einleitung
o Die Thermodynamik ist die Lehre von den
Umwandlungen der Energie.
Energie
o Beispiele für Anwendungsgebiete:
- Verbrennungsenergie wird in mechanische Arbeit
umgewandelt (Motoren)
- Elektrische Arbeit wird durch den chemischen
Transfer von Elektronen erzeugt (Batterien)
- Energetische Analyse chemischer Prozesse
(kann eine bestimmte Reaktion überhaupt
ablaufen ?)
- Bereitstellung von Energie zur Synthese
komplexer Biomoleküle
ü in Organismen
O
Bevor wir uns der Theorie hinter diesen Fragen widmen, benötigen wir
jedoch einige mathematische Hilfsmittel, die im Folgenden diskutiert
werden.
Zustandgrössen und - funktionen
o Zustandsvariabeln (Zustandsgrössen) sind physikalische Grössen,
mit denen man den Zustand eines makroskopischen Systems
beschreibt, z.B.
-Temperatur T
- Druck p
- Volumen V
- Stoffmenge n
- innere Energie U
und andere mehr (s. später)
1. Intensive Zustandsvariablen (Zustandsgrössen) sind Eigenschaften,
die von der Masse des Systems unabhängig sind.
z.B. Druck p, Temperatur T, Molvolumen Vm=V/n, Viskosität.
2.
Extensive Zustandsvariablen (Zustandsgrössen) sind Eigenschaften,
die von der Masse von System abhängig sind.
sind
z. B. Volumen V, Stoffmenge n, innere Energie U
Zustandgrössen und - funktionen
o Spezifische Grösse = Dividiert man eine extensive Grösse durch die Masse
m:
v=
V
m
o Molare Grösse = Dividiert man eine extensive Grösse durch die
Stoffmenge n:
Stoffmenge,
V
- molares Volumen
n
H
- molare Enthalpie
n
o Der Erfahrung nach werden für eine reine Substanz zwei intensive und
eine extensive Zustandsvariable benötigt, um ein System zu beschreiben.
Alle anderen Zustandsgrössen sind dann Zustandsfunktionen, die von den
gewählten Zustandsvariablen abhängen.
abhängen
Vm =
Hm =
o Extensive Grössen werden in intensive Grössen überführt.
o Prinzipiell hat keine der intensiven Grössen einen Vorrang vor der anderen.
o Oft verwendet man die Temperatur und den Druck als unabhängige
Variable
das molare Volumen ist eine Funktion von p und T !
Z t d ö
Zustandgrössen
und
d - funktionen
f kti
o Der Wert einer Zustandsvariable ist eine Funktion der anderen
Z t d
Zustandsvariablen,
i bl
eine
i Zustandsfunktion.
Z t d f kti
z. B. die innere Energie U kann als eine Funktion der unabhängigen
Zustandsgrössen
usta dsg össe p, T u
und
d n ausged
ausgedrückt
üc t werden:
e de U = f(T,p,n)
( ,p, )
o Zustandsgleichung = die Gleichung, die eine Beziehung zwischen den
Zustandsgrössen herstellt.
o Zustandfunktionen = Grössen eines Systems,
gegenwärtigem Zustand des Systems abhängen
die
nur
von
o Wegfunktionen = Grössen eines Systems, die weganhängig sind.
o Eine Zustandfunktion ist unabhängig davon, wie dieser Zustand erreicht
wurde
Partielle Ableitungen
Partielle Ableitung = Steigung der Funktion entlang einer Koordinate, wobei
alle anderen Koordinaten konstant gehalten werden.
werden
Beispiel: f = Funktion zweier unabhängiger Variabeln x, y
f(x,y)
- partielle Ableitung nach x bei konstantem y:
Schnitte parallel zur
(x,f)
Ebene
=
Funktionen von x und
y können abgeleitet
werden.
Partielle Ableitungen/ Totales Differential
f
- partielle Ableitung nach y bei konstantem x:
x= 0
⎛ δf ⎞
⎜⎜ ⎟⎟
⎝ δy ⎠ x
⎛ δf ⎞
⎜⎜ ⎟⎟
⎝ δy ⎠ x
x= l
x
y Schnitte parallel zur (y,f) Ebene
y
y
= Funktionen von x und y
können abgeleitet werden.
Das totale Differential df gibt die totale, infinitesimale Änderung einer Funktion
f(x,y) bei einer infinitesimalen Variation dx und dy der unabhängigen Variablen
x und y an. Totales Differential von f(x,y):
⎛ ∂f ⎞
⎛ ∂f ⎞
df = ⎜ ⎟ dx + ⎜⎜ ⎟⎟ dy
⎝ ∂x ⎠ y
⎝ ∂y ⎠ x
Gesamte Änderung des Funktionswerts >
Integral über df ist unabhängig vom Weg :
x1 , y1
∫ df
x2 , y 2
= f ( x1 , y1 ) − f ( x0 , y0 )
Grundbegriffe
o Das System = derjenige Teil der Welt, dem unser spezielles Interesse
gilt. Eine Region im Raum, die von der Umgebung durch die
S t
Systemgrenzen
abgegrenzt
b
t wird.
i d Die
Di Systemgrenzen
S t
sind
i d frei
f i wählbar,
ählb
aber nach der Wahl für die weitere Diskussion fixiert.
o Die Umgebung
g
g = Rest des Universums ((kann aber häufig
g auf einen
kleineren Teil des Labors beschränkt werden!)
o Das Weltall = System + Umgebung
o Systeme:
Offene
Systeme
Systeme,
Geschlossene
Abgeschlossene (Isolierte) Systeme:
Umgebung
System
Offen Sy.
Stoffe
Energie
Umgebung
System
Stoffe
Energie
Geschlossen Sy.
Systeme
Umgebung
System
und
Stoffe
Energie
Abgeschlossen Sy.
Arbeit Wärme,
Arbeit,
Wärme Energie
o Arbeit wird geleistet, wenn man einen Prozess dazu verwendend kann,
irgendwo in der Umgebung die Höhe eines Gewichtes zu verändern.
o Die Arbeit
> wird von dem System geleistet, wenn
das Gewicht angehoben wird
> wird an dem System geleistet, wenn
das Gewicht abgesenkt wird.
o Energie ist die Fähigkeit, Arbeit zu leisten
• wenn die Arbeit an dem System geleistet wird , nimmt seine Energie zu
• wenn das System Arbeit leistet > nimmt die Energie ab
o Wärmefluss = erfolgt die Änderung der Energie eines Systems aufgrund
einer
i
T
Temperaturdifferenz
t diff
o Behälter:
Wärme
diathermisch
Wärme
adiabatisch
Arbeit, Wärme, Energie
Vorgänge:
Wärme
1
1.
exoterme
2.
endotherme
exotherm
Wärme
endotherm
Molekularer Bild:
o Wärme: Energieübertragung durch eine ungeordnete Bewegung von
Molekülen (thermische Bewegung)
o Arbeit: Energieübertragung
ü
durch eine ordnete Bewegung von
Molekülen (mechanische Bewegung)
Energie
Wärme
Energie
Arbeit
Der erste Hauptsatz der TD
o Thermodynamik basiert auf vier grundlegenden Gesetzen (die Hauptsätze),
aus denen sich die gesamte Theorie entwickeln lässt.
o D
Der erste
t Hauptsatz
H
t t der
d TD = Wärme
Wä
und
d Arbeit
A b it sind
i d equivalent,
i l t wenn es
darum geht die Energie eines Systems zu ändern.
o Was für eine Energie
g eines Systems?
y
o Innere Energie (U) = die Gesamtenergie eines Systems (die Summe der
kinetischen und potentiellen Energie seiner Moleküle).
o Z. B. Die Innere Energie einatomiger Gase, die nur kinetische Energie
haben, ist:
Um = Um (0) + 3/2 RT
Wobei Um (0) ist die molare
Innere Energie bei T = 0K.
o Die Aenderung der Inneren Energie , wenn ein System von Anfangszustand
A (UA) in einen Endzustand E (UE) überführt wird,
wird ist:
∆ U = UE - UA
Der erste Hauptsatz der TD
o
Eigenschaften der Inneren Energie:
- U ist eine Zustandsfunktion
- Jede Änderung einer der Zustandgrössen (z.B. Druck) bewirkt eine
Änderung der Inneren Energie.
- U ist eine extensive Eigenschaft (hängt von der Stoffmenge ab).
o 1. Hauptsatz der TD (andere Formulierung) = In einem
abgeschlossenen
b
hl
S t
System
k
kann
k i
keine
Aenderung
A
d
d IInneren E
der
Energie
i
auftreten (U ist konstant)
Es ist noch nie gelungen
g
g
ein Perpetuum Mobile zu bauen !
Einheit für Innere Energie, Arbeit und Wärme: Joule (J) 1J = 1kg m2 s-2
Der erste Hauptsatz der TD
o 1. Hauptsatz der TD = Verändert sich ein System von einem Zustand
A in einen anderen Zustand E auf einem beliebigen, adiabatichen Weg, so
ist die geleistete Arbeit immer die gleiche.
wad = Arbeitsmenge, die geleistet wird in einem adiabatischen Prozess
(das System kann nicht Wärme austauschen)
wad = ∆U = U E − U A
∆U hat die gleiche Änderung auf nicht-adiabatischen Weg, aber die
geleistete Arbeit, w muss nicht dieselbe wie zuvor sein.
o Die aufgenommene Wärme, Q = den Unterschied zwischen der
geleisteten Arbeit und die Änderung der Inneren Energie:
Q = ∆U − w
w = Arbeitsmenge,
A b it
di geleistet
die
l i t t wird
i d in
i einem
i
nicht-adiabatischen
i ht di b ti h Prozess
P
(das System kann Wärme austauschen)
Der erste Hauptsatz der TD
o Wärme und Arbeit sind die Möglichkeiten die Energie eines Systems zu
beeinflussen.
o Mathematische Formulierung des erstes Hauptsatz der TD:
∆U = Q + w
Q = Wärme die dem System zugeführte
Energie
w = Arbeit die an einem System verrichtet ist
o Für infinitesimale Änderung des Systems:
dU
U = dQ
Q + dw
oMakroskopisch messbare Änderungen thermodynamischer Grössen
werden durch Integration über alle infinitesimalen Änderungsschritte
erhalten.
o Ein griechisches “ ∆” bezeichnet eine messbare makroskopische Änderung
der relevanten thermodynamischen Grösse, die nach der Integration über
alle infinitesimal kleinen Änderungen erhalten wird; wir lassen das “ ∆
∆” für Q
und w weg, weil der Transfer von Wärme und Arbeit immer bereits eine
Veränderung impliziert.
Wegfunktionen
ow > 0, Q > 0 wenn dem Systems Energie zugeführt wird.
o w < 0, Q < 0 wenn dem Systems Energie entnommen wird.
o w und Q sind Wegfunktionen (sind nicht totale Differentiale).
o Weggrössen (auch Transfergrössen) sind thermodynamische Grössen
deren Wert vom Weg abhängt, in dem das System in den gegenwärtigen
Zustand gelangt ist.
ist
o Möglichkeiten, einen thermodynamischen Prozess zu führen (“Wege”):
• isotherm: die Temperatur bleibt konstant
• isobar: der Druck bleibt konstant
• isochor: das Volumen bleibt konstant
• adiabatisch: kein Wärmefluss δq=0
Volumenarbeit
o Volumenarbeit = der Form von Arbeit, die mit einer Volumenänderung
verbunden ist.
o Die allgemeine Formulierung der Volumenarbeit = die Arbeit, die
erforderlich ist, um ein Objekt um eine Strecke dz gegen den Widerstand
einer
i
G
Gegenkraft
k ft F zu bewegen.
b
dw = − Fdz
o Das System hat eine Wand, die bildet
ein masseloser, reibungsfrei, starrer,
perfekt eingepasster
p
g p
Kolben der Fläche
A.
o Die
entgegen
der
Ausdehnung
wirkende Kraft ist:
F = pex A
pex
A
dz
A
pex
V l
Volumenarbeit
b it
o Wenn das System um die Strecke dz expandiert (gegen den äusseren
D k pex),
Druck
) ist
i t die
di Arbeit:
A b it
dw = − pex Adz
d = Adz
dV
Ad
dw = − pex dV
o Die Arbeit die insgesamt
g
bei der
Volumenänderung von VA auf VE verrichtet ist:
VE
w = − ∫ p ex dV
VA
o Für andere Formen der Arbeit, die wir nicht mechanische oder
zusätzliche Arbeit nennen wollen, gelten analoge Beziehungen, jeder
Arbeit, w ist:
w = (eine intensive Grösse) x (eine extensive Grösse)
A d
Andere
F
Formen d
der A
Arbeit
b it
o Oberflächenarbeit (bei Emulsionen):
γ dA
o Längenausdehnung (Spannung eines
Gummis):
fdl
γ = die Oberflächenspannung
dA = die Oberflächenänderung
f = die Spannung
dl = die Längeänderung
o Elektrische Arbeit:
φdφ
φ= das elektrische Potenzial
dφ = die Ladungsänderung