ε ε ε ε ε ε ε κ
Werbung

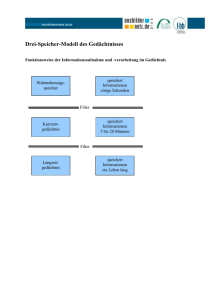
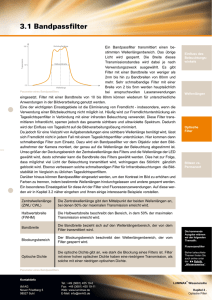
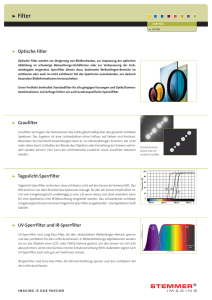
Instrumentelle Analytik Optische Materialien und Filter Seite N04_Materialien_a_BAneu.doc - 1/12 2.3 Optische Instrumentierung Der optische Spektralbereich erstreckt sich vom fernen IR-Gebiet bis zum Vakuum-UV Gebiet (1000 µm - 10 nm). Der für die Routineanalytik bedeutsame Spektralbereich umfasst aus physikalischen und messtechnischen Gründen aber nur den Wellenlängenbereich von ca. 25 µm (400 cm-1) bis ca. 170 nm (Mid-IR bis Quarz-UV). Im optischen Spektralbereich wird mit folgenden Analysemethoden gearbeitet: Atomemissions-Spektrometrie (AES) Atomabsorptions-Spektrometrie (AAS) Photolumineszenz-Spektrometrie UV/VIS-Absorptions-Spektrometrie (Spektralphotometrie) IR-Spektrometrie (MIR-Spektrometrie 4000 – 400 cm-1; NIR-Spektrometrie 12000 – 4000 cm-1) Raman-Spektrometrie 2.3.1 Eigenschaften optischer Materialien Mitentscheidend für die Leistungsfähigkeit eines Spektrometers ist die richtige Wahl der optischen Materialien, wie z.B.: Küvetten Filter Linsen, Spiegel Umlenkprismen (Strahlführungselemente, abbildende Elemente) Prismen, Gitter, Interferometer (dispersive Elemente) Wichtige Materialeigenschaften sind dabei: Brechzahl n Dispersion dn/d spektrale Transmission T() spektrales Reflexionsvermögen R() mechanische und chem. Stabilität (Härte, Korrosionsbeständigkeit, Temperaturverhalten etc.) 2.3.1.1 Brechungsindex (Brechzahl) Frequenzabhängigkeit der Brechzahl von Dielektrika1 Prinzipiell ist der Verlauf der Brechzahl n für alle Nichtleiter gleich. Die Brechzahl hat ihre physikalische Ursache in der Polarisation, die ein äußeres Wechselfeld erzeugt. D 0 r E 0 E P r 1 P 0E r n2 1 P 0E (nach der Maxwellrelation gilt r = n2) Wegen der Phasenverschiebung zwischen elektrischem Feld E und Materialpolarisation P ist die Dielektrizitätszahl r und damit die Brechzahl n( ) r komplex. n n' j 1 Im Anhang ist eine physikalische Begründung (klass. Dispersionstheorie) für das Frequenzverhalten von () gegeben. Instrumentelle Analytik Optische Materialien und Filter Seite N04_Materialien_a_BAneu.doc - 2/12 Setzt man die komplexe Brechzahl in die Wellenfunktion E(x,t) für eine Welle im Medium ein, erkennt man die Bedeutung von Real- und Imaginärteil. E E 0 sin(t kx ) mit k k0n k0 (n' j ) komplex: E Im[ E 0 exp j (t k 0n' x jk0x )] E Im[ E 0 exp( k 0x ) exp j (t k0n' x ) E Eˆ 0 exp( k0x) sin(t k0 n' x) Welle im Medium mit frequenzabhängiger Phasengeschwindigkeit c = /k = c0/n' Dispersion Abnahme der Amplitude beim Durchgang durch das Medium Absorption Bedeutung der komplexen Brechzahl: Der Realteil n' der Brechzahl bewirkt die Dispersion der Welle. Der Imaginärteil der Brechzahl bewirkt die Absorption der Welle. Typischer Verlauf der Brechzahl in Dielektrika Der Verlauf der Brechzahl hat in Isolatoren (Festkörper, Flüssigkeiten und Gase) einen typischen Verlauf, der wesentlich von den verschiedenen Resonanzen der Wechselwirkung der Strahlung mit der Materie beeinflusst ist. Außerhalb der Resonanzbereiche ist dn’/d immer positiv und << 1. Dies wird normale Dispersion genannt und ist für transparente Medien typisch. In der Nähe der Resonanzfrequenzen 0j ist dn/d < 0. Dies bezeichnet man als anomale Dispersion. n'( ) Realteil 1 01 02 ( ) Imaginärteil IR sichtbar UV Röntgen Instrumentelle Analytik Optische Materialien und Filter Seite N04_Materialien_a_BAneu.doc - 3/12 Rotationen Schwingungen elektronische Übergänge Abb.: Prinzipieller Verlauf von Real- und Imaginärteil der komplexen Dielekrizitätskonstante r als Funktion von der Frequenz. Minimum der Dispersion dn/d Materialien für das IR_ gebiet sind sehr oft: - hygroskopisch - zerbrechlich - giftig ! Abb.: Brechzahl einiger gebräuchlicher optischer Materialien für IR und UV/VIS Instrumentelle Analytik Optische Materialien und Filter Seite N04_Materialien_a_BAneu.doc - 4/12 2.3.1.2 Dispersion Die Wellenlängenabhängigkeit der Brechzahl n eines Materials wird in der Spektrometrie zur spektralen Zerlegung der Strahlung mit optischen Prismen ausgenutzt. Als Dispersion oder Brechungsdispersion bezeichnet man die Änderung der Brechzahl mit der Wellenlänge dn/d. Sie ist für die Größe der Aufspaltung von Spektrallinien in einem Prismenspektrometer entscheidend. Abb. rechts: Brechungsdispersion dn/d für verschiedene Prismenmaterialien Frage: Welches Glas eignet besonders gut für Prismenspektralapparate im VIS? Welche opt. Bauteile sollen möglichst geringe Dispersion besitzen ? 2.3.1.3 Transmission Die spektrale Durchlässigkeit (Transmission T) ist für Prismen, Fenster, Küvetten etc. ein wichtiges Kriterium. Für die verschiedenen Spektralbereiche verwendet man hauptsächlich folgende Materialien. VIS NIR MIR, FIR UV Vakuum-UV Optische Gläser (Kronglas, Flintglas; Quarzglas Optische Gläser (Kronglas, Flintglas; IR-Quarzglas - Infrasil) Halogene NaCl, LiF, KCl (Nachteil: geringe mech. Festigkeit, hygroskopisch) UV-Quarzglas - Suprasil, Saphir CaF2 (bis 130 nm) LiF (bis 110 nm) Die folgende Abb. zeigt die spektrale Durchlässigkeit T() für einige wichtige optische Materialien. Instrumentelle Analytik Optische Materialien und Filter Seite N04_Materialien_a_BAneu.doc - 5/12 Transmission einiger wichtiger optischer Materialien Abb.: Spektrale Durchlässigkeit T() einiger wichtiger optischer Materialien. Reflexionsverluste sind nicht berücksichtigt (Reintransmission). Instrumentelle Analytik Optische Materialien und Filter Seite N04_Materialien_a_BAneu.doc - 6/12 2.3.1.4 Reflexion Je nach Anwendung soll das Reflexionsvermögen besonders hoch sein (Spiegel) oder besonders niedrig sein (Linsen, Fenster, Küvetten). Bei durchsichtigen Stoffen und Metallen hängt die Reflexion von der Brechzahl n ab. Mit der komplexen Brechzahl n = n’ - j gilt für den Reflexionsgrad R bei senkrechtem Einfall. 2 R r 1 (n' j ) 2 1 (n' j ) 2 (n'1) 2 2 (n'1) 2 2 ; R T 1 Für Kronglas (n’ = 1,5, 0) beträgt R dann 4%, d.h. 4% der einfallenden Intensität werden reflektiert. Das Reflexionsvermögen ist für zunehmende Einfallswinkel von der Polarisation abhängig und erreicht bei streifendem Einfall 100%. Die Restreflexion von Glasoberflächen kann durch Aufdampfen einer dünnen Schicht mit der Brechzahl ng ns und der Dicke /4 in einem engen Wellenlängenbereich deutlich vermindert werden. Abb.: /4-Antireflexschicht Für das Metall Gold gilt bei = 589 nm: n’ = 0,37; = 4,9. Das ergibt ein Reflexionsvermögen von R = 94% und eine Eindringtiefe (x = 1/(2k0) der Welle von 10 nm. Zur Herstellung von Neutralfiltern (Absorptionsfilter zum Abschwächen von Strahlung) werden dünne Metallschichten (ca. 10 nm) auf ein Substrat aufgedampft. Abb.: Das spektrale Reflexionsvermögen einiger Metalle, die in der Optik für Spiegel verwendet werden. Instrumentelle Analytik Optische Materialien und Filter Seite N04_Materialien_a_BAneu.doc - 7/12 Die wichtigsten Eigenschaften der gebräuchlichsten optischen Materialien Instrumentelle Analytik Optische Materialien und Filter Seite N04_Materialien_a_BAneu.doc - 8/12 Filter und Spiegel Filter (Spiegel) dienen in der optischen Gerätetechnik zur Kontrolle, der von der gewünschten Wellenlänge abhängigen Transmission (Reflexion). Entsprechend den physikalischen Prinzipien unterscheidet man zwischen Absorptionsfiltern, Reflexionsfiltern (Spiegel) und dielektrischen Filtern und Spiegeln. Absorptionsfilter Bei Absorptionsfiltern (Neutralglasfilter und Farbfilter) wird die Absorption von chromophoren Gruppen, die in Trägermaterialien wie Glas oder Folien eingelagert sind, genutzt. Dielektrische Filter In der optischen Gerätetechnik werden überwiegend dielektrische Filter verwendet. Damit lassen sich Transmissions- und Reflexionskurven erreichen, die mit konventionellen Farbfiltern nicht realisierbar sind. Dielektrische Filter und Spiegel funktionieren nach dem Prinzip der Interferenz. Auf einem Glassubstrat sind dünne, /4 oder /2 dicke dielektrische Schichten aus LiF, MgF2, CaF2, oder Na3AlF6 (Kryolith) aufgedampft. Durch Variation von Dicke und Anzahl der Schichten können die Durchlassbereiche oder Reflexionsbereiche des Filters genau gewählt werden. Filterfunktionen, Filtertypen Kurzpass-Filter kurzwelliger Teil des Spektrums wird transmittiert, Rest wird absorbiert Langpass-Filter langwelliger Teil des Spektrums wird transmittiert, Rest wird absorbiert Kantenfilter Absorptionstyp Bandpassfilter Transmission eines schmalen Wellenlängenbereichs Antireflexfilter zur Vermeidung von störenden Reflexen dichroitische Filter ein Teil des Spektrums wird reflektiert, der andere Teil transmittiert, z. B.: dichroitische Langpass-, Kurzpass- und Bandpassfilter Wärmeschutzfilter: Transmission im VIS, Reflexion im IR Kaltlichtspiegel: Reflexion im VIS, Transmission im IR Dielektrisch Interferenzfilter Fabry-Perot-Etalon Interferenzfilter (dielektrisch) Glas-Farbfilter (Absorptionstyp) Schema eines dichroitischen Langpassfilters Instrumentelle Analytik Optische Materialien und Filter Seite N04_Materialien_a_BAneu.doc - 9/12 2.3.2 Wellenlängenzerlegung und Filterung in der Spektrometrie Filter und wellenlängendispersive Elemente (Gitter und Prisma) dienen in der Spektrometrie einerseits zur Isolation von bestimmten Spektralbereichen, andererseits zum Ausblenden unerwünschter Strahlung (Streustrahlung oder Spektren höherer Ordnung). Zum Einsatz kommen dabei hauptsächlich Absorptionsfilter (Farbglasfilter, Kantenfilter, Verlaufsfilter) Dichroitische Filter (Langpass, Kurzpass, Bandpass) Interferenzfilter (Fabry-Perot-Etalon) Monochromatoren (Prisma, Gitter) Emission: WZ SpektralFluorimeter Det Probe Absorption: WZ Lichtquelle Det Probe 2.3.2.1 Absorptionsfilter (Kanten- und Verlaufsfilter) Typische Transmissionskurven von a) Langpass-Kantenfilter b) Kurzpass-Kantenfilter Transmissionskurven handelsüblicher Kantenfilter (Schott) a) Langpass-Kantenfilter b) Kurzpass-Kantenfilter SpektralPhotometer Instrumentelle Analytik Optische Materialien und Filter Seite N04_Materialien_a_BAneu.doc - 10/12 rechts: Transmissionskurve eines Bandpassfilters (BP) (Kombination eines Kurzpass- und eines Langpassfilters) Relativ große spektrale Bandbreite (20 nm) und geringe Peak-Transmission Störeffekte: Bei UV-Bestrahlung zeigen einige Glasfilter Eigenfluoreszenz 2.3.2.2 Interferenzfilter (Fabry-Perot-Etalon FP) Mit Interferenzfiltern erreicht man besonders geringe Halbwertsbreiten der durchgelassenen Strahlung (typisch 1-10 nm bei ca. 50 % Transmission im Sichtbaren). Ein Fabry-Perot-Filter besteht aus zwei teildurchlässigen, planparallelen Metallschichten, zwischen denen sich ein dielektrisches Material der Dicke d und der Brechzahl n befindet. Einfallendes Licht einer bestimmten Wellenlänge wird durch Vielfachinterferenz verstärkt oder ausgelöscht. Abb.: Schema eines Interferenzfilters und Strahlengänge durch den Filter Verstärkung (konstruktive Interferenz) in Transmission: m 2d n 2 sin 2 Die Filter werden bei senkrechtem Einfall ( = 0) betrieben: m 2dn Zur Verdeutlichung sind die Strahlen geneigt gegen das Einfallslot gezeichnet.2 = 2dn heißt Gangunterschied und ist gleich dem optischen Wegunterschied zwischen den Teilstrahlen, die sich überlagern. Wenn der Gangunterschied ein ganzzahliges Vielfaches der Wellenlänge ist, verstärken sich die Teilstrahlen. 2 Instrumentelle Analytik Optische Materialien und Filter Seite N04_Materialien_a_BAneu.doc - 11/12 Abb.: Transmission eines Fabry-PerotInterferenzfilters mit einer Cavitydicke von d = 0,20 µm, n = 1,25 m 2dn 1 = 2 = 3 = Auflösung (Halbwertsbreite ) mF (die Größe F 4 R /(1 R) 2 heißt Finesse, R = Reflexion) 2 Kommerzielle Interferenzfilter mit dielektrischen Reflexionsschichten Bei Interferenzfiltern wird auf einem Glassubstrat ein Fabry-Perot als Schichtsystem aus dielektrischen Schichten aufgebaut. Zwei Spiegelschichten mit hoher Reflexion und eine dazwischen liegende Abstandsschicht der Dicke d bilden das Fabry-Perot. Die Spiegelschichten sind häufig dielektrische Spiegel (/4-HL-Stack). Eine Verbesserung der Filtereigenschaften (Bandbreite, Form der Durchlasskurve) erreicht man durch Hintereinanderschaltung von mehreren FP-Schichten mit unterschiedlichen Reflexionsgraden in sog. Multi-Cavity-Filtern. Die Variation von Reflexion und Abstandsschicht erlaubt so maßgeschneiderte Transmissionskurven. Typisch sind Filterbandbreiten von 1 - 10 nm bei einer Transmission von bis zu 80%. Da der Sperrbereich nicht über das ganze Spektrum ausdehnbar ist, werden zum „Blocken“ der unerwünschten Transmissionslinien zusätzliche Farbfiltergläser (sog. Kantenfilter) angekittet. Interferenzfilter sind meist gefasst, da die dielektrischen Schichtsysteme meist sehr feuchtigkeitsempfindlich sind. Die spiegelnde Schicht sollte immer in Richtung Lichtquelle zeigen (warum?). Abb.: Wirkungsweise einer λ/4-Reflexionsschicht Eine einfache λ/4-Schicht wirkt als “Spiegel“ bei der Wellenlänge λ, da sich die reflektierten Teilstrahlen verstärken. Zu beachten ist dabei der Phasensprung der Welle bei der Reflexion am optisch dichteren Medium. (Für n1 > n2 ändern sich bei der Reflexion die Phase um π.) Instrumentelle Analytik Optische Materialien und Filter Seite N04_Materialien_a_BAneu.doc - 12/12 Abb.: Schema eines MultilayerInterferenzfilters mit zwei Cavities. HLHLHL.. /4-Schichten wirken wie ein Spiegel. Alle Reflexe der /4-Schichten verstärken sich (Dielektrischer Spiegel). Abb.: Normalisierte Transmission eines FPInterferenzfilters mit 10 nm Bandbreite. Mit mehreren Cavities in einem Filter lassen sich Transmissionskurven mit flachem Top und steilen Flanken realisieren.3 Abb.: Transmission verschiedener Filter zur Wellenlängenselektion A: Fabry-Perot-Interferenzfilter (Primärbande - n = 1 - bei 700 nm geblockt) B: Multilayer-Interferenzfilter mit "Primärbande" bei 595 nm C: Handelsübliches Langpass-Kantenabsorptionsfilter D: Handelsübliches Bandpass-Filter (Kombination zweier Kantenfilter) E: Farbglasfilter 3 Durch einfaches Hintereinanderschalten von zwei Interferenzfiltern wird die Halbwertsbreite im Verhältnis 1/ 2 kleiner.