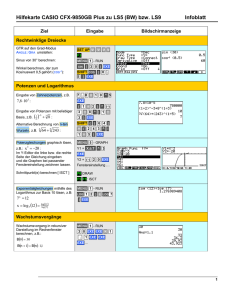
Übungen virtuelle Vorlesung KI - FB2

Übungen zur Virtuellen Vorlesung "Künstliche Intelligenz (KI)"
Prof. Dr. Peter Zöller-Greer
Übungen zum Kapitel "Aussagelogik"
1.
Man beweise oder gebe ein Gegenbeispiel:
a)
b)
c)
2.
Falls F -> G gültig ist und F gültig ist, so ist auch G gültig.
Falls F -> G gültig ist und F erfüllbar, so ist G erfüllbar.
|= ( [ |= (F∧G) ] -> [ |= (F -> G) ] )
An einem Belüftungssystem einer Industrieanlage soll eine Warnleuchte angebracht
werden, die aufleuchtet, wenn die Räume mangelhaft belüftet sind. Zur Belüftung stehen
vier unabhängige, jedoch in der Kapazität verschiedene Gebläse zur Verfügung, die im
Verbundsystem arbeiten (d.h. jedes System ist mit einem Raum verbunden). Über die
Kapazität der Größen ist folgendes bekannt:
a)
b)
Es müssen mindestens zwei Gebläse arbeiten
Sobald Gebläse A ausfällt, muß Gebläse B arbeiten, ansonsten reicht die
Belüftung nicht aus.
Konstruieren Sie eine möglichst einfache Schaltung, die die Warnleuchte einschaltet,
wenn der verbotene Zustand eintritt.
3.
Zur Bergung des Wracks "Charles the Lion" werden drei Hebewerke eingesetzt, ein
viertes und fünftes dient dazu, extreme Belastungen auszugleichen. Hierbei soll
folgendermaßen vorgegangen werden:
- Überschreitet die Belastung einen gewissen Wert (Sollwert) an mindestens einem
Hebewerk, so wird das vierte Hebewerk hinzugeschaltet.
- Wird der Sollwert an genau zwei Hebewerken Überschritten, so wird auch noch das
fünfte Hebewerk hinzugeschaltet.
- Sind alle drei Ausgangshebewerke überlastet, so ist die Bergung abzubrechen.
Entwickeln Sie für das vierte und fünfte Hebewerk eine geeignete Schaltung.
4.
Von zwei Krankheiten C und D und zwei Krankheitssymptomen S und T ist folgendes
bekannt:
a) Wenn der Patient an Krankheit C leidet und nicht an D, so muß er Symptom T
aufweisen.
b) Wenn mindestens eines der beiden Symptome auftritt, so leidet der Patient an
mindestens einer der beiden Krankheiten.
c) Tritt Symptom S nicht auf, so kann die Krankheit D nicht vorliegen.
d) Leidet der Patient an Krankheit D, aber nicht an C, so kann das Symptom T nicht
auftreten.
Welche Diagnose kann aufgrund dieser medizinischen Kenntnisse gegeben werden,
wenn der Patient (i) beide Symptome, (ii) nur Symptom S, (iii) nur Symptom T, (iv)
keines der beiden Symptome aufweist?
1
Übungen zur Virtuellen Vorlesung "Künstliche Intelligenz (KI)"
Prof. Dr. Peter Zöller-Greer
5.
Zeigen Sie formal, warum folgende Aussagen logische Probleme machen und worin
diese Probleme bestehen:
a)
Alles ist relativ
b)
Es gibt keine Wahrheit
c)
Weil es keinen absoluten Maßstab für Gut und Böse gibt, ist die Welt schlecht.
d)
Wenn Gott die Logik transzendiert, dann braucht sie für Gott nicht zu gelten.
Wenn also die Logik nicht gilt, dann muß auch nicht alles wahr sein was er uns
offenbart.
e)
Man kann über Gott keine Aussagen machen.
6
Nachfolgend ist jeweils eine Prämisse gegeben. Welche der darauffolgenden
Behauptungen sind relativ zu der Prämisse wahr?
a)
Prämisse: "Ein P ist nicht Q" sei falsch. Stimmt es dann, daß:
a1)
Ganz P ist Q
a2)
Kein P ist Q
a3)
Ein P ist Q
b)
6.
Prämisse: "Keine Religion ist völlig falsch" sei wahr. Stimmt es dann, daß:
b1)
Einige Religionen sind völlig falsch
b2)
Keine völlig falschen Dingen sind Religionen
b3)
Alle Religionen sind völlig falsch.
In der Philosophie wird seit Jahrtausenden über das sog. Theodizee-Problem
nachgedacht. Hierbei geht es um die logische Vereinbarkeit folgender zweier Aussagen:
a)
Es gibt einen allmächtigen und allgütigen Gott
b)
Es gibt (moralisch) Böses in der Welt
Die Frage, die sich also stellt, ist die, ob sich diese beiden Aussagen einander
widersprechen. Hätte ein allmächtiger, allgütiger Gott nicht eine bessere Welt als die
unsere schaffen können und sogar müssen? Oder anders ausgedrückt, ist eine bessere
Welt (in der z.B. alle freiwillig moralisch das Richtige tun) denkbar, die Gott hätte von
vorn herein schaffen können? Der große analytische Religionsphilosoph Alvin
Plantinga zeigt in seinem berühmten Buch "The Nature of Necessity", daß dies selbst
für einen allmächtigen, allgütigen Gott logisch unmöglich ist.
Für eine reine "Verteidigung" der Behauptung, daß sich a) und b) nicht widersprechen,
ist es aber bereits ausreichend, zu zeigen, daß es eine "logisch mögliche Welt" gibt in
der a) und b) gleichzeitig wahr sein können (in der wir dann offenbar leben). So etwas
nennt man "Logische Harmonisierung". Ein Beispiel so einer logischen Harmonisierung
ist die Frage, wie man die beiden nachfolgenden, zunächst widersprüchlich
erscheinenden Aussagen harmonisieren könnte:
c)
Es gibt keine Strafen
d)
Es kommen keine Diebstähle vor
Daß dies kein Widerspruch zu sein braucht läßt sich zeigen, in dem man eine mögliche
Welt annimmt, in der folgendes gilt:
e)
Alle haben genug und sind anständige Menschen
Damit stellt e) eine logische Harmonisierung von c) und d) dar (es handelt sich dabei
leider nicht um unsere derzeitige Welt...).
Wie könnte eine mögliche Harmonisierung von a) und b) aussehen?
2
Übungen zur Virtuellen Vorlesung "Künstliche Intelligenz (KI)"
Prof. Dr. Peter Zöller-Greer
Übungen zum Kapitel "Prädikatenlogik"
1.
Bilden Sie für nachfolgende Formeln jeweils (i) die bereinigte Pränexform und (ii) die
Skolemform und (iii) eine universell quantifizierte unvollständige minimale konjunktive
Normalform:
2.
Es sei folgendes Axiomensystem (=Wissenbasis) gegeben, wobei das Universum aus der
Menge aller PROGRAMMNAMEN besteht (Einträge in der FAT):
(1)"LAN.EXE" ist ein Programm
(2)"LAN.EXE" ist eine Software
(3)Jede Software ist virusinfiziert
(4)"WORD.EXE" ist ein Anwendungsprogramm
(5)Alle virusinfizierten Programme ließen "WORD.EXE" in Ruhe oder greifen es an
(6)Es gibt Programmnamen, die von allen anderen in ruhe gelassen werden
(7)Wenn Programme versuchen, Anwenderprogramme zu löschen, dann heißt das, das
diese Programme die Anwenderprogramme nicht in Ruhe lassen
(8)"LAN.EXE" versucht, "WORD.EXE" zu löschen
Zeigen Sie mit Hilfe des Resolutionstheorems unter Bildung von Resolventen die
Behauptung:
(9)"LAN.EXE" greift "WORD.EXE" an.
3.
Es sei folgendes Axiomensystem gegeben:
1.
2.
3.
4.
5.
6.
Hugo ist ein bekannter Schauspieler.
Karl ist ein Mensch und er ist auch schön.
Leider sind alle schönen Menschen auch eitel.
Wenn ein Mensch eitel ist, so will er nicht so sein wie Hugo oder er will ihm alles
nachmachen.
Menschen wollen so sein wie Schauspieler, falls sie diese mögen.
Karl mag Hugo.
Beweisen Sie mit Hilfe des Resolutionstheorems unter Bildung geeigneter Resolventen
die Aussage:
7.
Karl macht Hugo alles nach.
Hinweis: Es empfiehlt sich grundsätzlich, Axiome, die in konjunktiver Form sind, in
einzelne "Teilaxiome" zu zerlegen.
3
Übungen zur Virtuellen Vorlesung "Künstliche Intelligenz (KI)"
Prof. Dr. Peter Zöller-Greer
Übungen zum Kapitel "PROLOG"
1.
Tippen Sie die Beispiele aus der Vorlesung in einen Prologinterpreter ein und machen Sie
einige sinnvolle Testbeispiele damit.
2.
Schreiben Sie ein PROLOG-Programm zur (rekursiven) Bestimmung von n!.
3.
Schreiben Sie ein PROLOG-Programm zur rekursiven Bestimmung von sin(x) und cos(x)
ohne daß zu deren Berechnung spezielle Funktionen benutzt werden müssen (ANSATZ:
Eulers´sche Formeln im Komplexen und trigonometrische Additionstheoreme
ausnutzen).
4.
Stellen Sie sich vor, Sie wären Kellner in einem guten Restaurant. Eine Gruppe von
Gästen bestellt folgendermaßen:
Hans ist Antialkoholiker. Inge ißt weder Fisch noch Fleisch. Peter bestellt in Restaurants
grundsätzlich nur Pizza, während Sabine ein Schwäche für Scholle und Pizza hat. Sabine
hat keinen Durtst.
Trotz dieser unverschämten Art von Bestellung besitzen die Leute ein Minimum an
Tischsitten und würden daher niemlas Fisch ohne Wein oder gar alkoholische Getränke
zur Salatplatte bestellen.
Sie werfen Ihren PC an und schreiben hurtig ein PROLOG-Programm, welches Ihnen
ausgiebt, wer was essen und trinken will. Wie sieht diese PROLOG-Programm aus?
5.
Schreiben Sie ein PROLOG-Programm, welches mittels Listen-Operationen alle
Permutationen von 4 Elementen einer Liste ausgibt (jede Permutation wieder in einer
Liste).
6.
Schrieben Sie ein PROLOG-Programm, welches eine Liste "bereinigt": Wenn ein
Element einer Liste mehrfach auftaucht, so soll eine neue Liste erzeugt werden, welche
jedes Element nur noch einmal enthält.
7.
Schreiben Sie ein PROLOG-Programm zur Aufgabe 3 der Übungen zur Prädikatenlogik
(Seite 3).
4
Übungen zur Virtuellen Vorlesung "Künstliche Intelligenz (KI)"
Prof. Dr. Peter Zöller-Greer
Übungen zu den Kapiteln "Neuronale Netze, Genetische
Algorithmen und Fuzzy-Logik"
1.
Beschreiben Sie den Aufbau von Nervenzellen im Gehirn und deren Entsprechung bei
einem Neuronalen Netz. Welche Lernregeln kennen Sie?
(20 Punkte)
2.
Erläutern Sie den Begriff "Lineare Separabilität" und seine Bedeutung anhand des
XOR-Problems.
(20 Punkte)
3.
Es sei ein einfaches neuronales Netz (Perzeptron-Aufbau) der Form vorgegeben, daß es
2 Eingänge und 2 Ausgänge besitzt. Es sollen folgende 2 Muster trainiert werden:
E1
E2
A1
A2
0
1
1
1
1
0
0
0
Benutzen Sie ein einfaches lineares Gleichungssystem zur Berechnung der
Gewichtsmatrix und geben Sie diese an!
4.
Erläutern Sie das Roulette-Verfahren bei Genetischen Algorithmen. Wozu werden
genetische Algorithmen vorzugsweise eingesetzt?
5.
Was ist unter den Begriffen Zugehörigkeitsfunktion, linguistische Variable,
Konklusionsfunktion, Fuzzifizierung und Defuzzifizierung zu verstehen?
6.
Wozu werden Fuzzy-Systeme vorwiegend eingesetzt?
5