PDF, 87 KB

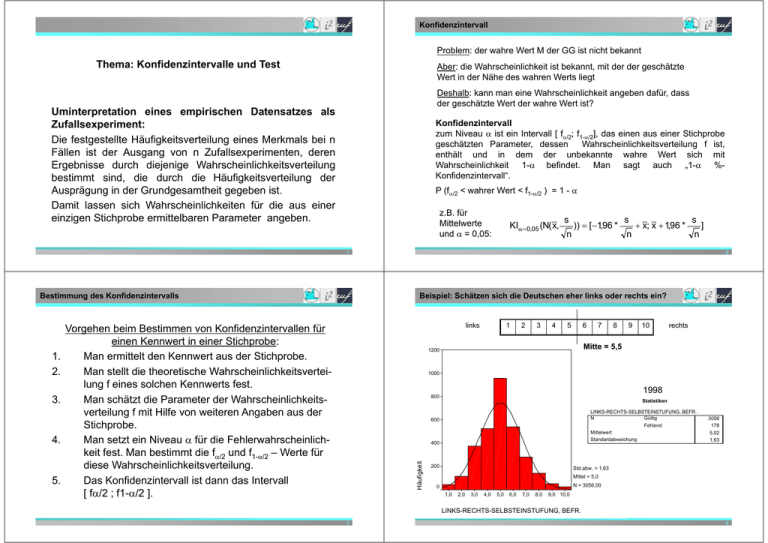
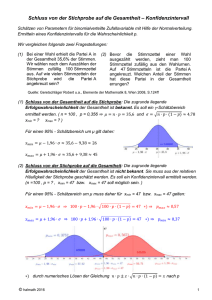
Konfidenzintervall
Problem: der wahre Wert M der GG ist nicht bekannt
Thema: Konfidenzintervalle und Test
Aber: die Wahrscheinlichkeit ist bekannt, mit der der geschätzte
Wert in der Nähe des wahren Werts liegt
Deshalb: kann man eine Wahrscheinlichkeit angeben dafür, dass
der geschätzte Wert der wahre Wert ist?
Uminterpretation eines empirischen Datensatzes als
Zufallsexperiment:
Die festgestellte Häufigkeitsverteilung eines Merkmals bei n
Fällen ist der Ausgang von n Zufallsexperimenten, deren
Ergebnisse durch diejenige Wahrscheinlichkeitsverteilung
bestimmt sind, die durch die Häufigkeitsverteilung der
Ausprägung in der Grundgesamtheit gegeben ist.
Damit lassen sich Wahrscheinlichkeiten für die aus einer
einzigen Stichprobe ermittelbaren Parameter angeben.
Müller-Benedict: Statistik I/8
Konfidenzintervall
zum Niveau  ist ein Intervall [ f/2; f1-/2], das einen aus einer Stichprobe
geschätzten Parameter, dessen
Wahrscheinlichkeitsverteilung f ist,
enthält und in dem der unbekannte wahre Wert sich mit
Wahrscheinlichkeit 1- befindet. Man sagt auch „1- %Konfidenzintervall“.
P (f/2 < wahrer Wert < f1-/2 ) = 1 - 
z.B. für
Mittelwerte
und  = 0,05:
1
4.
5.
n
))  [ 1,96 *
s
n
 x; x  1,96 *
s
n
]
Müller-Benedict: Statistik I/8
2
links
Vorgehen beim Bestimmen von Konfidenzintervallen für
einen Kennwert in einer Stichprobe:
Man ermittelt den Kennwert aus der Stichprobe.
Man stellt die theoretische Wahrscheinlichkeitsverteilung f eines solchen Kennwerts fest.
Man schätzt die Parameter der Wahrscheinlichkeitsverteilung f mit Hilfe von weiteren Angaben aus der
Stichprobe.
Man setzt ein Niveau  für die Fehlerwahrscheinlichkeit fest. Man bestimmt die f/2 und f1-/2 – Werte für
diese Wahrscheinlichkeitsverteilung.
Das Konfidenzintervall ist dann das Intervall
[ f/2 ; f1-/2 ].
1
2
3
4
5
6
7
8
9
10
rechts
Mitte = 5,5
1200
1000
1998
800
Statistiken
LINKS-RECHTS-SELBSTEINSTUFUNG, BEFR.
N
Gültig
Fehlend
Mittelwert
Standardabweichung
600
400
Häufigkeit
3.
s
Beispiel: Schätzen sich die Deutschen eher links oder rechts ein?
Bestimmung des Konfidenzintervalls
1.
2.
KI 0,05 (N( x,
200
3056
178
5,02
1,63
Std.abw. = 1,63
Mittel = 5,0
N = 3056,00
0
1,0
2,0
3,0
4,0
5,0
6,0
7,0
8,0
9,0 10,0
LINKS-RECHTS-SELBSTEINSTUFUNG, BEFR.
Müller-Benedict: Statistik I/8
3
Müller-Benedict: Statistik I/8
4
Beispiel: Lesekompetenz steigt mit Anzahl Büchern zu Hause
Einfacher Test
PISA 2000: Gymnasium
Unbekannte Varianz bei Mittelwertschätzungen
Ist die Varianz 2 der GG unbekannt, wird zur Schätzung von 2 die
Stichproben-Varianz s2 genommen. Bei großen Stichproben (n > 30) wird
das Konfidenzintervall des Mittelwerts mit der Normalverteilung
berechnet, sonst die t-Verteilung genommen.
How many
books at home
None
1-10
11-50
51100
101250
250500
> 500
535
520
547
561
574
586
595
None
1-10
11-50
51100
101250
250500
> 500
Lesekompetenz-Score
427
442
473
487
500
506,6
503,2
n (Anzahl)
84
649
2691
3033
2784
1504
921
69,4
67,2
67,9
65,4
68,7
69,7
71,7
Lesekompetenz-Score
PISA 2000: Realschule
How many
books at home
Test zum Niveau 
Ob sich ein aus einer Stichprobe geschätzter Kennwert einer GG von
einem vorgegebenen Wert unterscheidet, wird getestet, indem ermittelt
wird, ob sich der vorgegebene Wert innerhalb des Konfidenzintervalls
des geschätzten Werts zum Niveau alfa befindet oder nicht.
Liegt er innerhalb, so lautet das Test-Ergebnis: Kein Unterschied; liegt er
außerhalb, so lautet es: es besteht ein Unterschied (zum Niveau ). Man
sagt dann auch, der Unterschied ist signifikant (zum Niveau ).
Müller-Benedict: Statistik I/8
s (Standardabweichung)
Frage: Über 250 Bücher signifikante Unterschiede?
5
Beispiel: Kein Unterschied über 250 Bücher, Realschule
Müller-Benedict: Statistik I/8
6
Beispiel: Signifikanter Unterschied über 250 Bücher, Gymnasium
Univariate Statistiken
Univariate Statistiken
Internat. Lesen PV 1
How many books
at home - Q37
251-500
Mittelwert
95% Konfidenzintervall
des Mittelwerts
More than 500
Mittelwert
95% Konfidenzintervall
des Mittelwerts
Untergrenze
Obergrenze
Untergrenze
Obergrenze
Statistik
506,6510
503,1277
Standardf
ehler
1,79615
Internat. Lesen PV 1
510,1742
503,1859
498,5474
More than 500
2,36353
507,8244
510
Untergrenze
Obergrenze
Mittelwert
95% Konfidenzintervall
des Mittelwerts
Untergrenze
Obergrenze
Statistik
586,3326
583,9510
Standardf
ehler
1,21455
588,7142
594,7997
592,1865
1,33256
597,4129
595,0
95% CI Internat. Lesen PV 1
95% CI Internat. Lesen PV 1
Mittelwert
95% Konfidenzintervall
des Mittelwerts
597,5
512
508
506
504
502
592,5
590,0
587,5
585,0
500
582,5
498
251-500
251-500
More than 500
More than 500
How many books at home - Q37
How many books at home - Q37
Müller-Benedict: Statistik I/8
How many books
at home - Q37
251-500
7
Müller-Benedict: Statistik I/8
8
Konfidenzintervall für Anteile in kleinen Stichproben
Konfidenzintervall für Anteile in großen Stichproben
In Ihrer Klasse erreichen 6 von 23 Schülern = 26% Niveau 3.
Von 316 repräsentativ getesteten Schülern aus Vergleichsklassen
erreichen 98 = 31% das Niveau 3.
In Ihrer Klasse erreichen 6 von 23 Schülern = ein Anteil von 26% Niveau 3.
Die Klasse stelle eine repräsentative Stichprobe aller Ihrer Schüler dar.
Der Anteil von 26% kann dann als ein möglicher Indikator Ihrer
durchschnittlichen Lehrleistung angenommen werden.
In welchen Grenzen liegt mit 95% W. der „wahre“ Wert Ihrer Lehrleistung?
Niveau
Im Konfidenzintervall zum Niveau  für Anteile: KI = [ B(n,p)/2; B(n,p)1-/2].
Hier B(n, p) = B(23; 0,26);  = 5% = 0,05.
Klasse
Häufigkeit
Klasse
Anteil
Kleiner als 3
218
0,69
17
0,74
3
98
0,31
6
0,26
Summe
316
1
23
1
Haben in Ihrer Klasse weniger Schüler das Niveau 3 erreicht als im
Durchschnitt aller Vergleichsklassen?
Mit Tabelle: B(23; 0,26)0,025 ≈ 1, B(23; 0,26)0,975 ≈ 9 ,
KI = [ 1 ; 9 ] ,
mit 95% W. liegt der „wahre“ Wert Ihrer Lehrleistung zwischen 1 und 9
Schülern mit Niveau 3.
Müller-Benedict: Statistik I/8
Stichprobe Stichprobe
Häufigkeit Anteil
Der wahre Wert Ihrer Klasse ist 0,26 (Vollerhebung).
Der „wahre“ Wert aller Vergleichsklassen liegt im KI um 0,31.
KI für Anteile B(n; p); hier: n = 316, p = 0,31; Niveau  = 0,05
KI = [ B( 316; 0,31)0,025; B( 316; 0,31)0,975]
9
Müller-Benedict: Statistik I/8
10
Konfidenzintervall für Anteile, mit Laplace-Approximation
Satz von Laplace
In Ihrer Klasse erreichen 6 von 23 Schülern = 26% Niveau 3.
„Satz von Laplace/DeMoivre“
Sei B( n, ) eine Binomialverteilung und sowohl n >= 5 als auch n(1-)
>= 5 und n >= 10. Dann kann B(n, ) durch eine Normalverteilung
Der „wahre“ Wert aller Vergleichsklassen liegt mit 95 % W. in
KI = [ B( 316; 0,31)0,025; B( 316; 0,31)0,975]
approximiert werden.
  (1  )
)
n
für Anteile p:
B(n, )  N( ;
für absolute
Zahlen k:
B(n, )  N(n; n(1  )
Müller-Benedict: Statistik I/8
 [N( 0,31;
0,31 (1  0,31)
0,31 (1  0,31)
)0,025 ; N( 0,31;
)0,975 ]
316
316
= [ N( 0,31; 0,026)0,025; N( 0,31; 0,026)0,975 ]
= [ -1,96 · 0,026 + 0,31; 0,31 + 1,96 · 0,026 ]
= [ -0,051 + 0,31; 0,31 + 0,051]
= [ 0,259; 0,361] = [ 25,9%; 36,1%]
Test: Der Wert Ihrer Klasse (26%) liegt innerhalb des KI, also:
kein signifikanter Unterschied zu den Vergleichsklassen (bei
Sicherheitsniveau 95%)!
11
Müller-Benedict: Statistik I/8
12
Beispiel: Anteil Rechtsextremer
Bestimmung der Stichprobengröße
Wie groß muss eine Stichprobe für eine Anteilsbestimmung sein?
Folgende Angaben sind notwendig:
LINKS-RECHTS-SELBSTEINSTUFUNG, BEFR.
Gültig
Fehlend
Gesamt
LINKS
RECHTS
Gesamt
KA
Häufigkeit
45
114
375
525
956
539
283
143
53
23
3056
178
3234
Prozent
1,4
3,5
11,6
16,2
29,6
16,7
8,8
4,4
1,6
,7
94,5
5,5
100,0
Gültige
Prozente
1,5
3,7
12,3
17,2
31,3
17,6
9,3
4,7
1,7
,8
100,0
Kumulierte
Prozente
1,5
5,2
17,5
34,7
65,9
83,6
92,8
97,5
99,2
100,0
Wie genau soll der Anteil angebbar sein? (Länge des
Konfidenzintervalls, auf  x (rel. Anteil) genau)
Anteil „rechts“:
53+23 von 3056 =
2,5%
Wie sicher soll diese Genauigkeit sein? (-Niveau des
Konfidenzintervalls)
In welchem Bereich liegt der Anteil p ungefähr?
Dann sollte n mindestens sein:
p(1  p)
p(1  p)
]
 p; p  1,96 *
n
n
0,025(1  0,025 )
0,025(1  0,025 )
 [ 1,96 *
 0,025; 0,025  1,96 *
]
3056
3056
KI 0,05 ( Anteil p)  [ 1,96 *
z 
n  p  (1  p )  / 2 
 x 
2
Beispiel: erwarteter Anteil ca. 5%, Genauigkeit soll +/- 1% sein, Sicherheit 95%:
2
 1,96 
n  0,05  (1  0,05)  
  0,0475  38416  1824
 0,01 
= [ 0,0195; 0,0305] = [ 1,95%; 3,05%]
Müller-Benedict: Statistik I/8
13
Hausaufgabe:
Zum Nacharbeiten der Vorlesung vor den Hausaufgaben: Müller-Benedict, Kap. 9.1 – 9.4
1. In einer Population ziehen Sie eine Stichprobe der Größe 144. In dieser Stichprobe erreicht die Meinung über das "Vertrauen in die Schule" auf einer Skala
zwischen 1 = „überhaupt kein Vertrauen“ bis 7 = „vollstes Vertrauen“ einen Mittelwert m von 5,2 bei einer Standardabweichung von s = 1,2. Berechnen Sie ein
Konfidenzintervall, in dem der wahre Wert des Vertrauens der gesamten Population in die Schule mit 90% Wahrscheinlichkeit liegt.
2. Die Zahl von Ladendiebstählen liege in den USA bei durchschnittlich 60 (pro
Jahr und Geschäft) und sei normalverteilt. In Gotham City ermittelt eine repräsentative Untersuchung an 1000 Läden durchschnittlich 70 mit einer Standardabweichung von 40. Ist der Einsatz von Batman berechtigt, d.h. ist die Ladenkriminalität
in Gotham City höher als in den USA insgesamt ?
3. In einer Stichprobe von 100 Personen ergibt sich ein Anteil von 46 Frauen.
Stellt diese Anzahl noch eine „zufällige“ Abweichung von den erwarteten gleich
viel Männern und Frauen in der Population dar oder ist sie ein Hinweis auf
einen tatsächlichen niedrigeren Frauenanteil?
Müller-Benedict: Statistik I/8
15
Müller-Benedict: Statistik I/8
14