Die perfekte Welle ist ein Sinussignal
Werbung
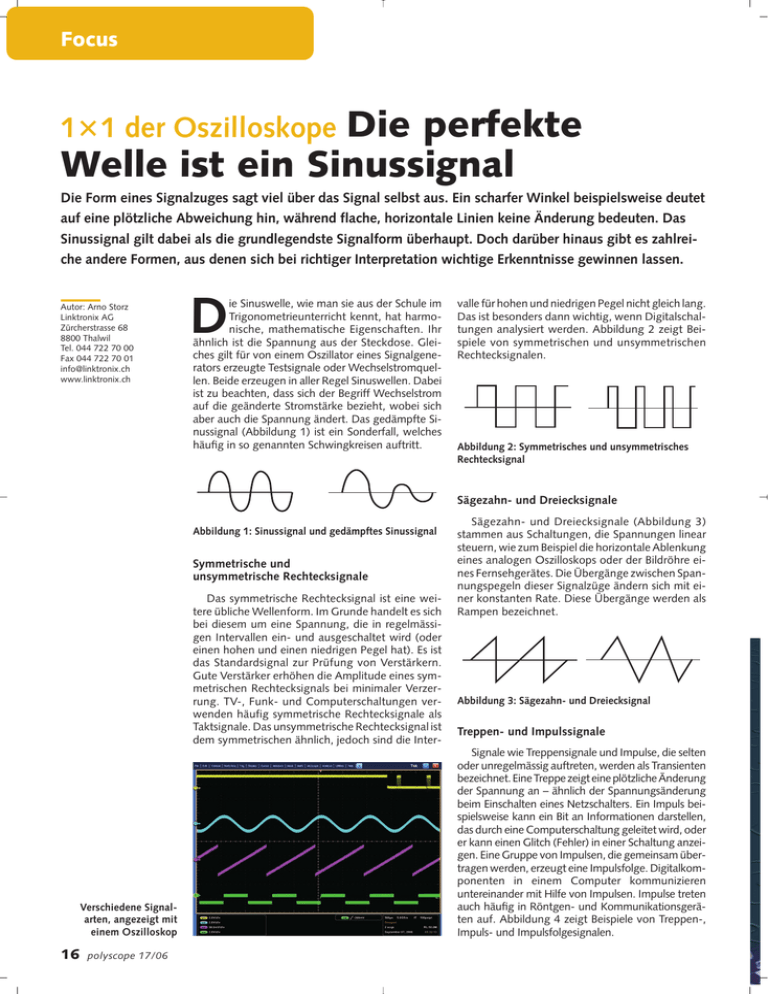
Focus Die perfekte Welle ist ein Sinussignal 1)1 der Oszilloskope Die Form eines Signalzuges sagt viel über das Signal selbst aus. Ein scharfer Winkel beispielsweise deutet auf eine plötzliche Abweichung hin, während flache, horizontale Linien keine Änderung bedeuten. Das Sinussignal gilt dabei als die grundlegendste Signalform überhaupt. Doch darüber hinaus gibt es zahlreiche andere Formen, aus denen sich bei richtiger Interpretation wichtige Erkenntnisse gewinnen lassen. Autor: Arno Storz Linktronix AG Zürcherstrasse 68 8800 Thalwil Tel. 044 722 70 00 Fax 044 722 70 01 [email protected] www.linktronix.ch D ie Sinuswelle, wie man sie aus der Schule im Trigonometrieunterricht kennt, hat harmonische, mathematische Eigenschaften. Ihr ähnlich ist die Spannung aus der Steckdose. Gleiches gilt für von einem Oszillator eines Signalgenerators erzeugte Testsignale oder Wechselstromquellen. Beide erzeugen in aller Regel Sinuswellen. Dabei ist zu beachten, dass sich der Begriff Wechselstrom auf die geänderte Stromstärke bezieht, wobei sich aber auch die Spannung ändert. Das gedämpfte Sinussignal (Abbildung 1) ist ein Sonderfall, welches häufig in so genannten Schwingkreisen auftritt. valle für hohen und niedrigen Pegel nicht gleich lang. Das ist besonders dann wichtig, wenn Digitalschaltungen analysiert werden. Abbildung 2 zeigt Beispiele von symmetrischen und unsymmetrischen Rechtecksignalen. Abbildung 2: Symmetrisches und unsymmetrisches Rechtecksignal Sägezahn- und Dreiecksignale Abbildung 1: Sinussignal und gedämpftes Sinussignal Symmetrische und unsymmetrische Rechtecksignale Das symmetrische Rechtecksignal ist eine weitere übliche Wellenform. Im Grunde handelt es sich bei diesem um eine Spannung, die in regelmässigen Intervallen ein- und ausgeschaltet wird (oder einen hohen und einen niedrigen Pegel hat). Es ist das Standardsignal zur Prüfung von Verstärkern. Gute Verstärker erhöhen die Amplitude eines symmetrischen Rechtecksignals bei minimaler Verzerrung. TV-, Funk- und Computerschaltungen verwenden häufig symmetrische Rechtecksignale als Taktsignale. Das unsymmetrische Rechtecksignal ist dem symmetrischen ähnlich, jedoch sind die Inter- Verschiedene Signalarten, angezeigt mit einem Oszilloskop 16 polyscope 17/06 Sägezahn- und Dreiecksignale (Abbildung 3) stammen aus Schaltungen, die Spannungen linear steuern, wie zum Beispiel die horizontale Ablenkung eines analogen Oszilloskops oder der Bildröhre eines Fernsehgerätes. Die Übergänge zwischen Spannungspegeln dieser Signalzüge ändern sich mit einer konstanten Rate. Diese Übergänge werden als Rampen bezeichnet. Abbildung 3: Sägezahn- und Dreiecksignal Treppen- und Impulssignale Signale wie Treppensignale und Impulse, die selten oder unregelmässig auftreten, werden als Transienten bezeichnet. Eine Treppe zeigt eine plötzliche Änderung der Spannung an – ähnlich der Spannungsänderung beim Einschalten eines Netzschalters. Ein Impuls beispielsweise kann ein Bit an Informationen darstellen, das durch eine Computerschaltung geleitet wird, oder er kann einen Glitch (Fehler) in einer Schaltung anzeigen. Eine Gruppe von Impulsen, die gemeinsam übertragen werden, erzeugt eine Impulsfolge. Digitalkomponenten in einem Computer kommunizieren untereinander mit Hilfe von Impulsen. Impulse treten auch häufig in Röntgen- und Kommunikationsgeräten auf. Abbildung 4 zeigt Beispiele von Treppen-, Impuls- und Impulsfolgesignalen. Focus Periodische und nicht periodische Signale Sich regelmässig wiederholende Signale werden als periodische Signale bezeichnet, während Signale, die sich laufend ändern, nicht periodische Signale genannt werden. Ein stabiles Signal auf einem Oszilloskop entspricht einem periodischen Signal, während ein bewegtes Bild einem nicht periodischen Signal entspricht. Spannungswellen Der allgemeine Begriff für ein Muster, das sich mit der Zeit wiederholt, ist Welle (bzw. Schwingung) – Schallwellen, Gehirnwellen, Meereswellen und Spannungswellen sind alle repetive Muster. Ein Oszilloskop misst Spannungswellen. Ein Zyklus einer Welle ist der Teil der Welle, der sich wiederholt. Ein Signalzug, auch als Kurvenzug oder einfach als Signal bezeichnet, ist die grafische Darstellung einer Welle. Ein Spannungssignalzug stellt die Zeit auf der horizontalen Achse und die Spannung auf der vertikalen Achse dar. Zusammengesetzte Signale Abbildung 4: Treppen-, Impuls- und Impulsfolgesignale Synchrone und asynchrone Signale Wenn zwischen zwei Signalen ein zeitlicher Zusammenhang besteht, werden diese Signale als synchron bezeichnet. Takt-, Daten- und Adressensignale in einem Computer sind Beispiele für synchrone Signale. Asynchron ist ein Begriff, mit dem Signale beschrieben werden, zwischen denen kein zeitlicher Zusammenhang besteht, wie zum Beispiel zwischen einem Tastendruck auf einer Computertastatur und dem Takt des Computers. Abbildung 5: Ein NTSC-Composite-Videosignal ist ein Beispiel eines zusammengesetzten Signals Einige Signale kombinieren die Charakteristiken von Sinussignalen, symmetrischen Rechteck- und Treppensignalen sowie Impulsen und erzeugen dadurch Signalzüge, die für viele Oszilloskope eine Herausforderung darstellen. Die Signalinformationen können in Form von Amplituden-, Phasen- und/oder Frequenzvariationen in die Signalzüge eingebettet sein. Deutlich wird das am Beispiel in Abbildung 5: Obwohl das Signal ein gewöhnliches Composite-Videosignal ist, besteht es aus vielen Zyklen von Signalzügen mit höherer Frequenz, die in eine Hüllkurve mit niedriger Frequenz eingelagert sind. In diesem Beispiel ist es in der Regel am wichtigsten, die relativen Pegel und das Timing der Treppensignale zu verstehen. Zur Darstellung derartiger Signale benötigt man ein Oszilloskop, das die niederfrequente Hüllkurve und die höherfrequenten Signalanteile entsprechend erfasst und überlagert darstellt, um eine adäquate visuelle Interpretation zu gewährleisten. Analoge und Digital- Phosphor-Oszilloskope eignen sich am besten zum Darstellen zusammengesetzter Signale wie z.B. Videosignale. Deren helligkeitsmodulierte Darstellung liefert die notwendigen Informationen über die statistische Häufigkeit einzelner Signalkomponenten, die zum Verständnis der tatsächlichen Signalereignisse erforderlich sind.