Lösungsblatt 10 ausgegeben am 18. 06. 2007

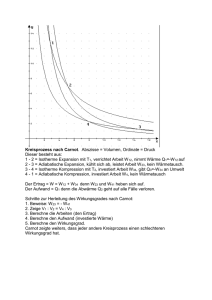
3
Lösungen
Lösung zu 65. (a) Siehe Abbildung 1.
(b) Schritt I: freie adiabatische Expansion, also ist δW = 0, δQ = 0 und damit
T2 = T1 . Folglich ist nach 1. Hauptsatz auch ∆U = 0.
Schritt II: isobare Kompression, also ist δQ = cp ∆T = cp (T1 − T3 ) und ∆W =
−nR(T1 − T3 ). Zur Vervollständigung noch ∆U = δQ + δW = cp (T1 − T3 ) −
nR(T1 − T3 )
Schritt III: isochore Erwärmung, heisst Volumen konstant, also dV = 0 und
damit keine verrichtete ArbeitδW = 0. Dann ist δQ = ∆U = cV (T1 − T3 ).
Die verrichtete Arbeit ergibt sich also nur aus Schritt II.
(c) Bei einem irreversiblen Prozess muss
I
δQ
<0
T
Abbildung 1: Der Mayersche Kreisprozess.
4
gelten. Also jetzt einfach Einsetzen:
I
Z
Z
Z
δQ
δQ
δQ
δQ
=
+
+
T
T
T
T
I
II
ZT3
= 0+
ncp
III
dT
+
T
T1
ZT1
ncV
dT
T
T3
T1
T3
+ ncV ln
T1
T3
T1
= (cV − cp ) · n · ln
<0
T3
= ncp ln
Das Ergebnis ist kleiner Null, da T1 > T3 und cV < cp ist.
Lösung zu 66. Zunächst eine Nebenrechnung zur Bestimmung der Anzahl der Mole
3 · 105 mN2 · 0.5m3
p1 V1
n=
=
= 42.65mol
J
RT
8.314 mol·K
· 423K
kJ
kJ
cp = 1.005 kg·K
und damit Cp = 29.1 kmol·K
.
dQ = nCV dT + pdV
und
∆S = nCV ln T2 T1 + nR ln
V2
V1
Man beachte auch noch
Cp − CV = R
V2
T2 p1
=
V1
T1 p2
Dann folgt
∆S = S2 − S1 = nCV ln
p2
V2
T2
p2
+ nCp ln
= nCp ln
− nR ln
p1
V1
T1
p1
Jetzt die bekannten Größen einsetzen:
∆S = 42.65mol·29.1
kJ
293
J
0.8
J
·ln
−42.65mol·8.314
·ln
= 12.97
kmol · K
423
mol · K
3
K
Das Endvolumen ergibt sich dann zu
V −2=
42.65 · 8.314 · 293 3
nRT2
=
m = 1.299m3
5
p2
0.8 · 10
5
Abbildung 2: Zu Aufgabe 68: Die Fläche unter der Kurve ist die zugeführte Wärme,
was der Entropieänderung entspricht
Lösung zu 67. Die Längenänderung des Bandes beträgt ∆l = l0 · α · ∆T . Sei ε die relative
Längenänderung ε = ∆l
= l0 α∆T
und F = A · E · ε.
l0
l0
F = 2 · 10−4 m2 · 206 · 109
N
1
· 1.2 · 10−5 · 280K = 138.4kN
2
m
K
Lösung zu 68. Gegeben sind m = 100g. Das sind 3.453mol Luft. p = 2bar, T1 = 293K, T2 =
J
J
383K, cp = 29.1 mol·K
und cV = cp − R = 20.79 mol·K
. Die Entropiedifferenz
ist
∆S21 = S2 − S1
V2
= ncp ln
V1
weil isobar (p1 = p2 ) erwärmt wird.
∆S21 = ncp ln
T2
T1
= 34.53 · 29.1J · K −1 ln
383
= 269.2J · K −1
293
∆Q = ncp (T2 − T1 )
383
kJ
cdot ln
= 0.710
K
293
= 90.45kJ
6
Abbildung 3: Zu Aufgabe 68: Die Fläche 1-2-b-d entspricht der gesamten zugeführten
Wärme. Die Fläche a-2-b-c entspricht der Wärme, die zur Erhöhung der inneren Energie ∆U erforderlich ist. Die Fläche d-1-2-a-c entspricht der in Arbeit umgewandeltem
Wärme.
Teilweise wird die Wärme in Volumenarbeit umgewandelt
W12 = nR(T2 − T1 ) = 0.287
kJ
(383 − 293)K = 25.83kJ
K
Die Entropiedifferenz bei konstantem Volumen, also der Anteil der Entropiedifferenz, der sich für die Änderung der inneren Energie ergibt, ist
∆S = S2 − S1 = ncV ln
T −2
383
= 0.719kJ · K −1 · ln
= 0.193kJ · K −1
T1
293
Lösung zu 69. Der Carnot-Prozess wurde schon mehrmals behandelt und daher als bekannt angenommen. Es gilt
T2 − T1
= −m · cV
dW = dQ ·
T2
µ
¶
T2
− 1 dT
T1
Die Temperaturen bestimmen dabei den Wirkungsgrad der Carnot-Maschine.
Die Dichte von Wasser sei hier mit 1kg pro Liter angenommen. Also haben 5
7
Liter die Masse 5kg. Die Arbeit findet man dann durch Integration:
ZT0
W = −mcV
T2
dT + mcV
T
dT
T2
T2
= mcV T2 ln
ZT0
T2
− mcV (T2 − T0 )
T0
= 5kg · 4.18kJ kg −1 K −1 · 298K · ln
298
− 5kg · 4.18kJ kg −1 K −1 · 25K = 23.2kJ
273
der Wirkungsgrad η bestimmt sich aus den angegebenen Temperaturen
η=
T2 − T1
= 0.0839
T2
Nun muss man noch beachten, dass die Kristallisations- bzw. Schmelzwärme
aufgebracht werden muss.
ΛS = 5kg · 333.1
kJ
= 1.67M J
kg
Für die Überführung dieser Wärme ist die Arbeit W = QS · η = 1.67M J ·
0.0839 = 140.8kJ erforderlich.
Die Gesamtarbeit ist also Wges = 175.6kJ.
Lösung zu 70. Zunächst allgemeines zur Entropie. Die Entropie ist eine Zustandsfunktion. Sie
ist für eine reversible infinitesimale Zustandsänderung eines Stoffsystems bei
der Temperatur T durch die Aufnahme der Wärmemenge δQ definiert.
dS =
δQ
T
Die Änderung zwischen zwei Zuständen 1 und 2 ist gegeben durch
Z2
∆S = S2 − S1 =
δQ
T
1
Allgemeines zur Entropie:
1. Bei einem reversiblen Prozess bleibt die Entropie konstant.
2. Für ein ideales Gas ergibt sich für eine reversible Zustandsänderung
dS =
dU + pdV
dV
δQrev
=
+R
T
T
V
8
Für eine Isobare:
∆Sisobar = CV ln
T2
V2
+ R ln
T1
V1
∆Sisochor = Cp ln
T2
p2
− R ln
T1
p1
Für eine Isochore:
Für den Kreisprozess nach Carnot:
(a) isotherme Kompression (1 nach 2)
Z
Z
Z
δQ
pdV
dV
V2
S2 − S1 =
=
= nR
= nR ln
T
T
V
V1
(b) adiabatische Expansion (2 nach 3):
Z
S3 − S2 =
δQ
=0
T
(c) isotherme Expansion (3 nach 4):
Z
Z
Z
δQ
pdV
dV
V4
S4 − S3 =
=
= nR
= nR ln
T
T
V
V3
(d) adiabatische Kompression (4 nach 1):
Z
δQ
S1 − S4 =
=0
T
Als Summe über alle Änderungen der Entropie ergibt sich:
∆S = nR ln
V2
V4
+ 0 + nR ln
+0
V1
V3
Für adiabatische Prozesse gilt
T2 · V1κ−1 = T1 · V2κ−1
und
T1 · V3κ−1 = T2 · V4κ−1
Division der beiden Gleichungen ergibt:
V2
V1
=
V4
V3
umgeformt auch
V2
V3
=
V4
V1
und noch logarithmiert
− ln
V2
V4
= ln
V3
V1
9
Also folgt jetzt
∆S = nR ln
V2
V4
+ 0 + nR ln
+0=0
V1
V3
Lösung zu 71. Es erfolgt keine Wärmeaustausch, also handelt es sich um eine adiabatische Zustandsänderung.
Volumina:
V1 = A · l1 = πr2 · l1 = 0.0157m3
V2 = πr2 · l2 = 0.00942m3
Die Temperatur ist 293K, p1 = 105 mN2 , κ = 1.4. Mit dem 1. Hauptsatz findet
sich
Q12 = mcV (T2 − T1 ) − W12 = 0
Also
W12 = mcV (T2 − T1 )
Für Adiabaten gilt
pV κ = const
µ ¶κ−1
V2
T1
=
T2
V1
µ ¶κ
V2
p1
=
p2
V1
µ ¶ κ−1
T1
p1 κ
=
T2
p2
mit κ =
cp
cV
und cp − cV = R. Dann weiter
W12 = ncV (T2 − T1 ) = n
R
(T2 − T1 )
κ−1
1
(p2 V2 − p1 V1 )
κ − 1 µµ ¶
¶
p1 V1
T2
=
−1
κ−1
T1
õ ¶ κ−1
!
p1 V1
p2 κ
=
−1
κ−1
p1
!
õ ¶
κ−1
p1 V1
V1
− 1 = 890N m
=
κ−1
V2
=
10
Die Endtempertaur nach der Verdichtung ist
T2
=
T1
µ
V1
V2
¶κ−1
= 1.227
Also T2 = 359.5K = 86.5◦ C. Der Endruck beträgt
µ ¶κ
p2
V1
=
= 2.04
p1
V2
Also ist der Enddruck p2 = 2.04bar.
Lösung zu 72. Zunächst nutzen wir den 1. und 2. Hauptsatz und finden:
dS =
δQ
1
p
= dU + dV
T
T
T
Die Zustandsgleichungen umgeformt ergeben
1
mcV
=
T
U
p nR
T V
Das wir oben eingesetzt
µ
R dV
dU
+
dS = m cV
U
mm V
¶
Integration vom Ausgangszustand bis zum aktuellen, also von z0 (U0 , V0 , m) bis
z(U, V, m) ergibt
µ
¶
U
R
V
S(U, V, m) = S0 + m cV ln
+
ln
U0 m m V 0