01a.Das negative Zweierkomplementzahlensystem.Junold

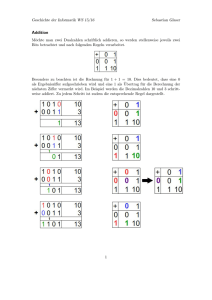
Das negative
Zweierkomplementzahlensystem
Ines Junold
23. Februar 2010
1
Inhaltsverzeichnis
1 Einleitung
3
2 Das
2.1
2.2
2.3
konventionelle Zweierkomplement
Definition . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Addition und Subtraktion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Multiplikation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4
4
4
4
3 Das
3.1
3.2
3.3
negative Zweierkomplementsystem
Definition . . . . . . . . . . . . . . . . .
Addition und Subtraktion . . . . . . . .
Multiplikation . . . . . . . . . . . . . . .
3.3.1 Booth-Verfahren . . . . . . . . .
3.3.2 Baugh-Wooly-Verfahren . . . .
5
5
5
6
6
8
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
4 Zusammenfassung
10
5 Literaturverzeichnis
11
2
1 Einleitung
Das Zweierkomplement wird bei gebrochenen Festkommazahlen zur Implementierung der
digitalen Signalverarbeitung auf VLSI-Chips verwendet. Allerdings wird bei der digitalen
Signalverarbeitung häufig der Wert 1 benötigt. Das Problem hierbei ist jedoch, dass im
konventionellen Zweierkomplement diese Zahl nicht dargestellt werden kann. Dies führt
zu dem Problem, dass −1 × −1 das Resultat +1 ergibt, welches nicht als gebrochene Zweierkomplementzahl dargestellt werden kann. Es bedeutet auch, dass der Absolutwert von
−1 nicht dargestellt werden kann.
Aus diesem Grund entwickelte Swartzlander (vgl. Swartzlander 2007) das sogenannte negative Zweierkomplement (Abb. 1). Seit 1990 unterrichtet er an der Universität von Texas
in Austin als Professor für Elektrotechnik und Computer Engineering. Er besitzt einen
Abschluss in Elektrotechnik an der Purdue Universität, der Universität von Colorado und
der Universität von Kalifornien. Bei seiner Forschung liegt der Schwerpunkt auf einem
anwendungsspezifischen Prozessordesign mit einer Hochgeschwindigkeitscomputerarithmetik.1
Abbildung 1: Earl E. Swartzlander, jr.
1
vgl.http://www.reviews.com/masthead/masthead_editors.cfm?editor=swartz
3
2 Das konventionelle Zweierkomplement
2.1 Definition
Durch das konventionelle Zweierkomplement besteht die Möglichkeit, auch negative Zahlen im Dualsystem darstellen zu können. Der Wertebereich liegt in −(2n−1 ), ..., 0, ..., 2n−1 −1,
wobei n der Anzahl der Bits entspricht. Stehen beispielsweise 8 Bit zur Verfügung, dann
erstreckt sich der Zahlenbereich von −128(10) bis +127(10) .
Darstellung und Umwandlung der Binärzahlen in das konventionelle Zweierkomplement
sind sehr einfach zu implementieren. Zuerst muss ein Vorzeichenbit festgelegt werden.
Handelt es sich bei der umzuwandelnden Zahl x um eine positive, so wird das Vorzeichenbit auf 0 gesetzt. Ist es jedoch negativ, also x < 0, so werden alle Bits invertiert bzw.
gekippt. Danach muss nur noch der Wert der Quantisierungsstufe 2k addiert werden. Die
Quantisierungsstufe wird auch als Least Significant Bit (LSB) bezeichnet.
Am Beispiel der Zahl −2.2510 wird die Umwandlung nun gezeigt.
2.2510
¬[010.01]2
2−2 = 0.2510
101.102 + 000.012
=
=
=
=
010.012
101.102
0.012
101.112
Umwandlung vom Dezimal- ins Binärzahlensystem
Invertierung der einzelnen Bitstellen
Berechnung der Quantisierungsstufe
Addieren der Quantisierungsstufe
2.2 Addition und Subtraktion
Bei Addition und Subtraktion muss keine Fallunterscheidung vorgenommen werden, da
die Subtraktion auf die Addition zurückgeführt werden kann.
S = A − B = A + (−B)
Die Summe S = (sn−1 , sn−2 , ..., s0 ) besteht aus den zwei Summanden A = (an−1 , an−2 , ..., a0 )
und B= (bn−1 , bn−2 , ..., b0 ). Somit ergibt sich die folgende Bildungsvorschrift:
s i = ai ⊕ b i ⊕ c i
Die Variable ci bezeichnet den Übertrag an der Stelle i. Die Bildungsvorschrift hierfür
lautet:
ci+1 = (ai ∧ bi ) ∨ (ai ∧ ci ) ∨ (bi ∧ ci ), wobei c0 = 0
Der entsprechende Schaltkreis, ein Volladdierer, ist in Abbildung 2 dargestellt.
2.3 Multiplikation
Im Gegensatz zur Addition und Subtraktion muss bei der Multiplikation eine Erweiterung des Wertebereichs vorgenommen werden, da das Ergebnis meist nicht im Wertebereich der Faktoren liegt. Die Stellenanzahl wird dabei verdoppelt und der Wert des
Most Significant Bit (MSB) entsprechend oft vor den ersten Faktor gesetzt. Somit ist die
neue Stellenanzahl bei einem Faktor mit n Bit Stellen 2n. Hierfür eignet sich ein Serienoder Parallelmultiplizierer. Die Funktionsweise der verschiedenen Multiplizierer wird im
Kapitel 3.2 Rechenoperationen dargestellt.
4
Abbildung 2: Volladdierer
3 Das negative Zweierkomplementsystem
3.1 Definition
Das negative Zweierkomplement ist im Grunde genommen nur eine Spiegelung des bekannten und in Kapitel 2 beschriebenen konventionellen Zweierkomplements. Aus Abbildung
3 geht hervor, dass die Umwandlung ins negative Zweierkomplement über das Invertieren
aller Bits außer dem Vorzeichenbit möglich ist. Die resultierenden Zahlen sind der Größe
nach geordnet (zum Beispiel die Kleinste ist 0000, die Größte 1111 und die Zwischenwerte
sind intuitiv geordnet). Die Schwierigkeit besteht darin, die n − 1 Bits für jede Zahl zu
kippen. Eine Alternative zum Invertieren ist nur das Vorzeichenbit zu invertieren. Dann
sind die Zahlen invers der Größe nach geordnet. Nach dem Vergleich ist das Ergebnis invertiert (zum Beispiel wenn der Vergleich A > B ergibt, ist das korrekte Ergebnis A < B).
Das negative Zweierkomplement einer Zahl kann durch die nachfolgende Formel berechnet
werden.
n−2
R = rn−1 − ∑ ri 2i−n+1
i=0
Die umzuwandelnde, gebrochene n Bit lange Zahl besitzt das Vorzeichenbit rn−1 , wobei
R die gegebene Zahl im negativen Zweierkomplement beschreibt. Dies soll am folgenden
Beispiel gezeigt werden. Die zu berechnende Zahl sei 85 .
R = 1 − (0 ∗ 20−(4+1) + 1 ∗ 21−(4+1) − 1 ∗ 22−(4+1) )
R = 1 − 1 ∗ 2−2 + 1 ∗ 2−3
R = 1 − 0, 25 + 0, 125
R = 1 − 0, 375
R = 85
3.2 Addition und Subtraktion
Die Rechenoperationen Addition und Subtraktion sind im negativen Zweierkomplement
gleich den Rechenregeln im konventionellen Zweierkomplement. Darum soll ein Beispiel
für die Addition genügen.
5
Abbildung 3: Vergleich vom negativen Zweierkomplement mit dem konventionellen
Zweierkomplement
1
2
+ 83
1.100
+ 1.101
= 1.001
=
7
8
Auch die Subtraktion kann - wie beim konventionellen Zweierkomplement - auf die Addition zurückgeführt werden. Nur muss auch hier der Divisor negiert werden. Dies geschieht
äquivalent zum konventionellen Zweierkomplement am Beispiel von 14 .
0.2510
¬[1.110]2
0.0012 + 0.0012
= 1.1102
= 0.0012
= 0.0102
Umwandlung vom Dezimal- ins Binärzahlensystem
Invertierung der einzelnen Bitstellen
1 am LSB addieren
3.3 Multiplikation
Es gibt zwei Arten von gebräuchlichen Multiplikatoren, die sequenziellen und die parallelen Multiplikatoren. Für beide Versionen kann man die Implementierung im negativen
Zweierkomplement zeigen.
3.3.1 Booth-Verfahren
Die sequenzielle Multiplikation ist im Allgemeinen im Booth-Verfahren (oder im modifizierten Booth-Verfahren) realisiert. Diese werden durch Sequenzen von Additionen,
Subtraktionen und Shift- Operationen verwirklicht. Da bereits äquivalente Operationen
für Addition und Subtraktion gezeigt wurden, ist das negative Zweierkomplement mit
Booth-Verfahren ähnlich dem konventionellen Booth-Verfahren. Der einzige Unterschied
sind die vertauschten Additions- und Subtraktionsoperationen.
6
Multiplikator Bits
00
01
10
11
konventionelle Zweierkomplement Bemerkung
P =P
laufende Folge von Nullen
P =P +B
Ende einer Folge von Einsen
P =P −B
Anfang einer Folge von Einsen
P =P
laufende Folge von Einsen
Operationen des Booth-Verfahrens im konventionellen Zweierkomplement
Multiplikator Bits negative Zweierkomplement Bemerkung
00
P =P
laufende Folge von Nullen
01
P =P −B
Ende einer Folge von Einsen
10
P =P +B
Anfang einer Folge von Einsen
11
P =P
laufende Folge von Einsen
Operationen des Booth-Verfahrens im negativen Zweierkomplement
Dies wird am folgenden Beispiel deutlich. Zunächst werden die Operationen anhand der
Zweiersequenzen bestimmt:
A ∗ B = 34 ∗ 85 = 1.010 ∗ 1.0110
1.0110 → Addieren und Shift
1.0110 → No-OP und Shift
1.0110 → Subtrahieren und Shift
1.0110 → Addieren (und Shift)
Danach müssen die einzelnen Arbeitsschritte des Multiplikators betrachtet werden. Mit
Hilfe der einzelnen Additions-, Subtraktions- und Shift-Operationen wird aus dem Multiplikand und dem Multiplikator das Produkt errechnet:
Initialisierung P = 0 0.000
10: ADD A
1.010
1.010
Shift P
1.1010
11: No-OP
1.1010
Shift P
1.11010
01: SUB A
0.110
0.10010
Shift P
0.010010
10: ADD A
1.010
No-Shift
1.100010
Dies soll als Nachweis der sequentiellen Multiplikation im negativen Zweierkomplements
genügen.
7
3.3.2 Baugh-Wooly-Verfahren
Die parallelen Multiplizierer hingegen werden durch eine die modifizierte Variante des
Baugh-Wooly-Verfahrens. Es werden dabei Regeln zur Vereinfachung des Multiplikationsschemas angewandt2 . Daraus ergibt sich folgendes Bild:
Zweierkomplement Baugh- Wooly- Multiplizierer
×
A5 B5
P10
−A5 B4
−A4 B5
P9
−A5 B3
A4 B4
−A3 B5
P8
−A5 B2
A4 B3
A3 B4
−A2 B5
P7
−A5 B1
A4 B2
A3 B3
A2 B4
−A1 B5
P6
−A5
−B5
−A5 B0
A4 B1
A3 B2
A2 B3
A1 B4
−A0 B5
P5
A4
B4
A4 B0
A3 B1
A2 B2
A1 B3
A0 B4
A3
B3
A3 B0
A2 B1
A1 B2
A0 B3
A2
B2
A2 B0
A1 B1
A0 B2
A1
B1
A1 B0
A0 B1
A0
B0
A0 B0
P4
P3
P2
P1
P0
Änlich wie bei den Seriellen Multiplizierern wird die Umwandlung in das negative Zweierkomplement nur durch eine Vertauschung der Vorzeichen erreicht. Der daraus resultierende Multiplizier sieht dann folgendermaßen aus:
Negatives Zweierkomplement Baugh- Wooly- Multiplizierer
×
−A5 B5
P10
2
A5 B4
A4 B5
P9
A5 B3
−A4 B4
A3 B5
P8
A5 B2
−A4 B3
−A3 B4
A2 B5
P7
A5 B1
−A4 B2
−A3 B3
−A2 B4
A1 B5
P6
−A5
−B5
A5 B0
−A4 B1
−A3 B2
−A2 B3
−A1 B4
A0 B5
P5
A4
B4
−A4 B0
−A3 B1
−A2 B2
−A1 B3
−A0 B4
A3
B3
−A3 B0
−A2 B1
−A1 B2
−A0 B3
A2
B2
−A2 B0
−A1 B1
−A0 B2
A1
B1
−A1 B0
−A0 B1
A0
B0
−A0 B0
P4
P3
P2
P1
P0
vgl.
http://www2.informatik.uni-jena.de/~nez/rechnerarithmetik_5/Folien/
Rechnerarithmetik.2008.16.handout.pdf S. 18ff.
8
Anhand eines 4 Bit Multiplizierers kann man die Funktionalität verdeutlichen:
3
4
5
8
15
32
≡
≡
=
1. 0 1
×
1. 0 1
1. 1 0
1. 1 0 1
0. 1 1 1
0. 0 1 0.
1 1 1
1. 1 0 0 0 1
0
1
1
1
0
4 Zusammenfassung
Im Kapitel »Einleitung« wurde beschrieben, dass besonders in der digitalen Signalverarbeitung der Wert 1 benötigt wird. Swartzlander (vgl. Swartzlander 2007) stellt diese Zahl
durch sein negatives Zweierkomplement zur Verfügung, jedoch ist in diesem Zahlensystem
der Wert −1 nicht verfügbar. Dies würde bedeuten, dass jedes Mal, wenn in einer Rechnung
der Wert 1 oder −1 benötigt wird, die erforderlichen Zahlen in das jeweilige Zahlensystem
umgewandelt werden müssen. Und somit ist das negative Zweierkomplement nur dann
sinnvoll, wenn die 1 häufiger benötigt wird als die −1.
9
5 Literaturverzeichnis
1. Swartzlander, E.: The Negative Two?s Complement Number System. Austin 2007
2. Zehendner, E.: Rechnerarithmetik. Jena 2008
3. http://wapedia.mobi/de/Zweierkomplement
10