energieerhaltungssatz die kinetische energie
Werbung

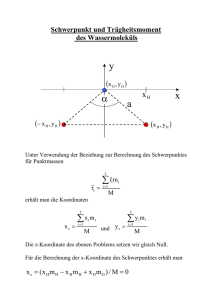
Physik f. Erdwissenschaften E. Kneringer Experimentalphysik 12. Vorlesung 1. Mechanik B. Dynamik 15. November 2005 PfE Übersicht: MECHANIK A. Kinematik: z v v v r (t ), v (t ), a (t ) Wichtiger Spezialfall: Beschleunigung a = const (auch 0) 1-dim. Bewegungen 2-dim. Bewegungen z Unabhängigkeit der Bewegungen in x- und y-Richtung? B. Newton’sche Dynamik: Die 3 Newton‘schen Axiome Kräfte Gravitationskraft z Federkraft z 15.11.2005 Impuls und Impulserhaltung Arbeit, Energie und Energieerhaltung Drehbewegungen 2 PfE Arbeit, Energie E = ∫ F⋅ds Skalarprodukt: ist gleich 0, falls Kraft und Weg senkrecht zueinander sind Potentielle Energie z E = mg(h2 – h1) z Wenn man sich entlang von Äquipotentialflächen bewegt, dann wird (im Idealfall) keine Arbeit geleistet Kinetische Energie z E = ∫ F⋅ds = ∫ ma⋅ds = ∫ m⋅dv/dt⋅ds = ∫ m⋅dv⋅ds/dt = ∫ m⋅v⋅dv = mv2/2 Federenergie z E = ∫ kx⋅dx = kx2/2 15.11.2005 h1 wird meist 0 gesetzt x … die Auslenkung aus der Ruhelage 3 PfE Energieerhaltung Beispiel: Bungee-Jumping 15.11.2005 Potentielle Energie → Kinetische Energie → Federenergie 4 PfE Rotationen Die lineare Geschwindigkeit hängt vom Abstand von der Drehachse ab. v = ωr ω … Winkelgeschwindigkeit (oder Kreisfrequenz) Z.B. doppelter Abstand → doppelte Geschwindigkeit v ω ϕ ω dϕ ω= dt 15.11.2005 5 PfE 15.11.2005 6 PfE 15.11.2005 7 PfE Rotation und kinetische Energie v1 Bekannt aber v4 1 1 2 ∑ mi (ωri ) = ω 2 ∑ mi ri 2 2 i 2 i m3 r1 m1 ω r4 r3 r2 v2 m2 v3 dies schreiben wir als E = I ω2/2 mit dem Trägheitsmoment I = ∑i miri2 15.11.2005 m4 vi = ωri E= 1 E = ∑ mi v i2 i 2 r ist der Normalabstand von der Drehachse 8 PfE Trägheitsmomente Kugel und Zylinder 2 I = MR 2 5 Vollkugel mit Masse M und Radius R, R mit der Drehachse durch den Mittelpukt. I= R 15.11.2005 1 MR 2 2 Vollzylinder (oder Scheibe) mit Masse M und Radius R, Drehachse = Achse des Zylinders. 9 PfE Experiment: rollende Zylinder 15.11.2005 Der hohle Zylinder ist langsamer als der Vollzylinder, weil er das grössere Trägheitsmoment besitzt, nämlich I = MR2 (Annahme: die gesamte Masse befindet sich im Abstand R von der Achse) 10 PfE Nochmals rollende Zylinder Gleiche Zylinder oder Räder verschiedener Grösse sind gleich schnell. 15.11.2005 Beweis: Übungsaufgabe 11 PfE Energieerhaltung Verschiedene Körper rollen eine schiefe Ebene hinunter. Verwende die Energieerhaltung um die Endgeschwindigkeit zu berechnen. Energie vorher: Potentielle Energie z Energie nachher: Kinetische Energie + Rotationsenergie z 15.11.2005 12 PfE Rotierender Stuhl Jemand sitzt auf einem rotierenden Stuhl, die Arme ausgesteckt und ein Gewicht in jeder Hand. Das gesamte Trägheitsmoment sei anfangs Ia , und die Winkelgeschwindigkeit sei ωa . Dann bringt die Person ihre Hände an den Körper und das neue Trägheitsmoment sei Ie . Wie gross ist am Ende die neue Winkelgeschwindigkeit ωe? ωe ωa Ia 15.11.2005 Ie 13 PfE Antwort Da keine externen Kräfte/Drehmomente wirken, gilt die Drehimpulserhaltung. La = I aωa = Le = I eωe Wie steht es mit der Energieerhaltung? Ea ,e = 15.11.2005 ⇒ ωe I a = ωa I e I a ,eωa ,e 2 2 Ee I eωe Ia = = 2 E a I aω a Ie 2 ⇒ Rotationsenergie nimmt zu, falls das Trägheitsmoment kleiner wird. Woher kommt die Energie? vgl. Übungsaufgabe ‘Schaukel’ 14