Page 1 Physik PHB3/4 (Schwingungen, Wellen, Optik

Physik PHB3/4 (Schwingungen, Wellen, Optik)
09_Schwingungen_Einführung_BA_W2000.doc - 1/4
II SCHWINGUNGEN
1 Einführung
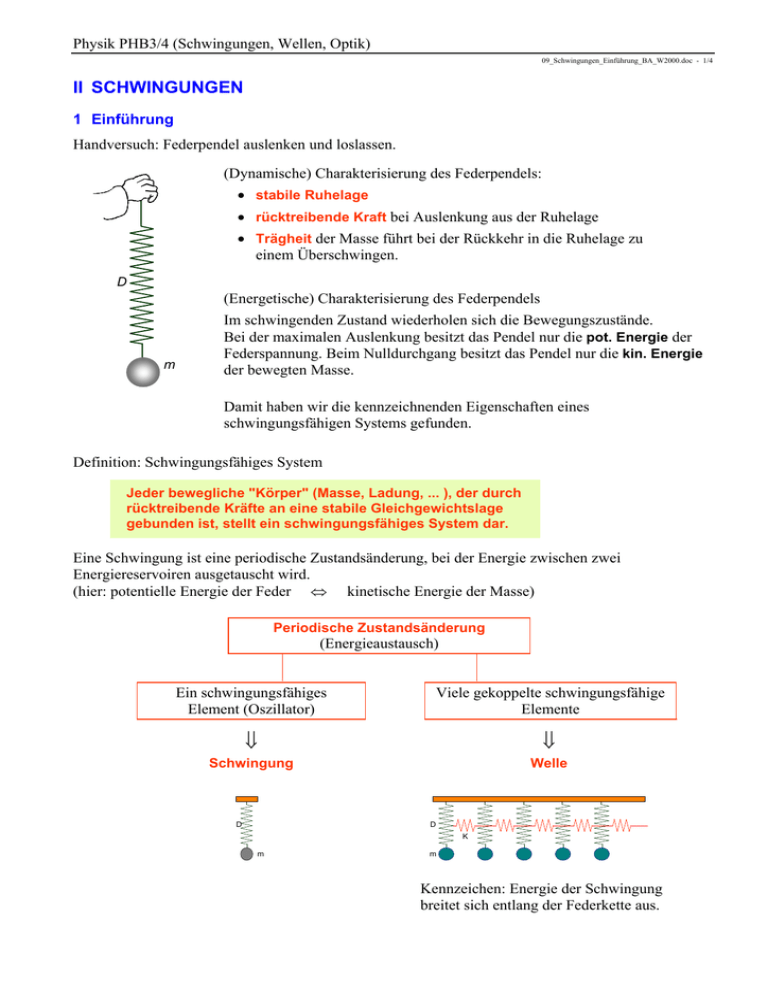
Handversuch: Federpendel auslenken und loslassen.
(Dynamische) Charakterisierung des Federpendels:
 stabile Ruhelage
 rücktreibende Kraft bei Auslenkung aus der Ruhelage
 Trägheit der Masse führt bei der Rückkehr in die Ruhelage zu
einem Überschwingen.
D
(Energetische) Charakterisierung des Federpendels
m
Im schwingenden Zustand wiederholen sich die Bewegungszustände.
Bei der maximalen Auslenkung besitzt das Pendel nur die pot. Energie der
Federspannung. Beim Nulldurchgang besitzt das Pendel nur die kin. Energie
der bewegten Masse.
Damit haben wir die kennzeichnenden Eigenschaften eines
schwingungsfähigen Systems gefunden.
Definition: Schwingungsfähiges System
Jeder bewegliche "Körper" (Masse, Ladung, ... ), der durch
rücktreibende Kräfte an eine stabile Gleichgewichtslage
gebunden ist, stellt ein schwingungsfähiges System dar.
Eine Schwingung ist eine periodische Zustandsänderung, bei der Energie zwischen zwei
Energiereservoiren ausgetauscht wird.
(hier: potentielle Energie der Feder  kinetische Energie der Masse)
Periodische Zustandsänderung
(Energieaustausch)
Ein schwingungsfähiges
Element (Oszillator)
Viele gekoppelte schwingungsfähige
Elemente


Schwingung
Welle
D
D
K
m
m
Kennzeichen: Energie der Schwingung
breitet sich entlang der Federkette aus.
Physik PHB3/4 (Schwingungen, Wellen, Optik)
09_Schwingungen_Einführung_BA_W2000.doc - 2/4
2 Systeme mit 1 Freiheitsgrad
2.1 Definitionen und Begriffe
a) Freiheitsgrad
Zahl der notwendigen Koordinaten zur vollständigen Beschreibung des
Bewegungsablaufs eines Systems.
Beispiel: Massenpunkt 3 Translationsfreiheitsgrade f = 3;
Starrer Körper 3 Translations- plus 3 Rotationsfreiheitsgrade f = 6
b) Periodische Bewegung
Nach einem Zeitintervall T (Periodendauer) wiederholt sich ein bestimmter Bewegungszustand
in gleicher (ungedämpfte Schwingung) oder ähnlicher (gedämpfte Schwingung) Form.
Beispiel für eine periodische Bewegung
(t): physikalische Größe
 (t)
T
(Auslenkung, Ladung, Spannung etc. )
(t )  (t  T )  (t  2T ) ...
t
T:
Periodendauer
Wichtigster Spezialfall einer periodischen Bewegung:
Harmonische Schwingung - der Schwingungsvorgang läßt sich mit einer einfachen Sinus- bzw.
Kosinusfunktion beschreiben. (Wir werden sehen, dass sich eine harmonische Schwingung immer
dann ergibt, wenn die rücktreibende Kraft einem linearen Kraftgesetz gehorcht).
c) Kinematik der harmonischen Schwingung (Wiederholung)
Nach obiger Definition ist eine Kreisbewegung mit der Winkelgeschwindigkeit  = 2/T = const
eine periodische Bewegung mit der Periode T ( zirkulare Schwingung).
Eine lineare Schwingung, d.h. eine Bewegung auf einer geraden Bahn ergibt sich durch Projektion auf
die x- oder y-Achse.
y
y
r
r

0
x
r
x
T/2

Projektion auf y-Achse:
y ( )  r sin 
y (t )  r sin t

Projektion auf x-Achse:
x( )  r cos 
x(t )  r cos t


T

t

Physik PHB3/4 (Schwingungen, Wellen, Optik)
09_Schwingungen_Einführung_BA_W2000.doc - 3/4
Weg- Zeitgesetz der harmonischen Schwingung
s (t )  sˆ sin t
mit:
s = Amplitude
t =  = Phase (entspricht dem Dreh winkel,
bzw. dem Bogen auf dem Einheitskreis)
 = Kreisfrequenz, [] = rad/s
f = Frequenz
t = Zeit
2
Wegen:  
 2f
äquivalente Schreibweise
T
2
s(t )  s sin( t )  s sin(2ft )
T
s(t)
s
t
0
T/2
T
v(t)
Geschwindigkeit
ds
dt
v (t )  s cos t
v (t ) 
mit
vmax  s  v
t
0
T/2
T
a(t)
Beschleunigung
dv d 2 s

dt dt 2
a (t )   s 2 sin t   2 s(t )
a (t ) 
mit
t
amax  s 2  a
T/2
T
s(t)
Allgemeine Form einer harm. Schwingung
s(t )  s sin(t  0 )
0 = Phase für t = 0
(Nullphasenwinkel)
t
Physik PHB3/4 (Schwingungen, Wellen, Optik)
09_Schwingungen_Einführung_BA_W2000.doc - 4/4
d) Darstellung von Schwingungsvorgängen mit komplexen Zahlen
Darstellung mit kreisenden Zeigern oder Phasoren in der komplexen Ebene
Vorteil: Einfache Mathematik, kein umständliches Rechnen mit trigonometrischen
Umformungen, anschauliche Darstellung bei Überlagerung von Schwingungen.
(t ) sei eine beliebige komplexe Zahl1
 exp{ j (t   )}
(t )  
0
Im
ˆ e j 0 exp{ jt}
 (t )  
ˆ e j 0
C
(t)
t
Interpretation:
(t ) geht aus C durch Drehung um den Winkel
C

Re
t hervor. (t ) beschreibt eine Bewegung auf
 und der
dem Kreis mit dem Radius 
Winkelgeschwindigkeit .
Zusammenhang mit reeller Schwingung
 exp{ j (t   )}
(t )  
0
komplexe Darstellung
 Re{exp j (t   )}
(t )  
0
Projektion auf reelle Achse
______________________________________________________
 cos(t   )
(t )  
0
reelle Kosinusschwingung
 exp{ j (t   )}
(t )  
0
komplexe Darstellung
 Im{exp j (t   )}
(t )  
0
Projektion auf imaginäre Achse
______________________________________________________
 sin(t   )
(t )  
0
reelle Sinusschwingung
Projektion von  (t ) auf die reelle Achse
 Kosinusschwingung
Projektion von (t ) auf die imaginäre Achse  Sinusschwingung
e) Darstellung mit Eulerformel
Nach Euler gilt:
e jt  cos t  j sin t
2 cos t  e jt  e  jt
2 j sin t  e jt  e  jt
1
Diese Darstellung (unterstrichen) verwendet man in der Elektrotechnik zur Kennzeichnung einer komplexen Größe.