Übung 6, Aufgaben (zum 20.5.2013)
Werbung
MST
Mathematik 2
Übung 6
Prof.Dr.B.Grabowski
(Anwendung komplexer Zahlen: LFZ von Polynomen und Schwingungen)
I. Darstellung von Schwingungen als komplexe Zeiger
Aufgabe 1
Skizzieren Sie den Verlauf folgender Funktionen im kartesischen Koordinatensystem:
a) 3 cos 2 x
b) 2 sin 3 x
3
4
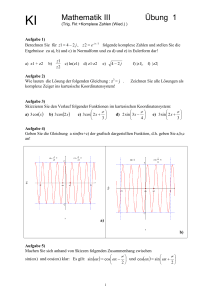
Aufgabe 2
Geben Sie die Gleichung a sin(bx+c) der grafisch dargestellten Funktion, d.h. geben Sie a,b,c
an!
a)
b)
Aufgabe 3
Machen Sie sich anhand von Skizzen folgenden Zusammenhang zwischen
sin(x) und cos(x) klar: Es gilt: sin x cos x und cosx sin x
2
2
Aufgabe 4
Eine harmonische (sinus-)Schwingung Asin t an der Stelle t kann als Imaginärteil der
komplexen Zahl z(t) = Ae j (t ) aufgefasst werden.
D.h., jeder Schwingung Asin t kann man eindeutig die komplexe Zahl
z (t) = Ae j (t ) Ae j e jt zuordnen. z(0)= Ae j wird als komplexer Scheitelwert der
Schwingung bezeichnet.
Eine harmonische (sinus-)Schwingung Asin x wird in der Technik üblicherweise als
komplexer Zeiger z(0)= Ae j dargestellt. charakterisiert, mit welcher Frequenz dieser
Zeiger im Koordinatensystem entgegengesetzt dem Urzeigersinn herumsaust. (siehe Skizze).
1
Mathematik 2
MST
Übung 6
Prof.Dr.B.Grabowski
(Anwendung komplexer Zahlen: LFZ von Polynomen und Schwingungen)
Darstellung der Schwingung
Asin t
als komplexer Zeiger
a) Stellen Sie folgende Schwingungen als komplexe Zeiger dar ( =314 s-1)!
a1) u1(t) = 100V sin(t),
a2) u2(t) = 150Vcos(t - /4)
(Hinweis: cosinus erst in den sinus umwandeln!)
b) Stellen Sie folgende komplexen Zeiger als Schwingungen dar!
b1) 2e
j
4
, =3
b2) 3e
j
3
, =2
Aufgabe 5
Bestimmen Sie die durch additive Überlagerung (Superposition) aus den beiden
gleichfrequenten Wechselspannungen y1(t) und y2(t) entstehende resultierende
Wechselspannung y(t) = y1(t) + y2(t) über die Methode der Komplexifizierung ( =314 s-1)!
y1(t) = 100V sin(t),
y2(t) = 150Vcos(t - /4)
Zeichnen Sie y1(t), y2(t) und y(t) als komplexe Zeiger und verdeutlichen Sie sich damit
grafisch die Bedeutung der Rechenmethode !
Aufgabe 6
Ermitteln Sie ausschließlich grafisch (Darstellung und Addition der komplexen Zeiger) und
nicht rechnerisch die Überlagerungen y(t) = A sin(2t + ) mit
y(t) = 3sin(2t - /2) + 4 cos(2t - /2)
d.h. bestimmen Sie A und .
2
MST
Mathematik 2
Übung 6
Prof.Dr.B.Grabowski
(Anwendung komplexer Zahlen: LFZ von Polynomen und Schwingungen)
II. Funktionen – allgemeine Eigenschaften
Aufgabe 7
Welche der folgenden Abbildungsvorschriften sind Funktionen, welche nicht?
(D = Definitionsbereich, B = Bildbereich)
1.
y 2 x, x D, y B , D B ℝ
2.
3.
4.
5.
y 2 x, x D, y B, D x x R x 0, B ℝ
y 2 x, x D, y B, D x x R x 0, B y y ℝ y 0}
y x 2 , x D, y B , D B ℝ
y x 2 , x D, y B, D {x x ℝ x 0}, B=ℝ
Aufgabe 8
Für welche der folgenden Funktionen sind injektiv, surjektiv und/oder bijektiv?
a) y 5 x 5 , D B ℝ
b) y 9 x 4 , D 3 , 3 , B [0,3]
6
c) y x 1, D ℝ, B [1, )
2
d) y 5 3 x 2 , D [ , ), B [0, )
3
5
e) y = 5x , D=[0,), B=ℝ
f) y = 5x5, D=B=[0,)
Aufgabe 9 Zeichnen Sie das Bild der Abbildung r 2(1 cos( )) für 0 180 im
Polarkoordinatennetz!
Aufgabe 10
a) Wie lautet die parametrische Gestalt x=x(t), y=y(t) der Funktion y=3x-7 ?
b) Geben Sie die in parametrischer Form gegebene Funktion x(t) = 3t+1, y(t)=4t2+5
in der expliziten analytischen Form y=f(x) an!
c) Wie lautet die parametrische Gestalt x=x(t), y=y(t) der Kreisgleichung x2 + y2 = 4?
Aufgabe 11
Folgende Skizze zeigt das Prinzip einer einfachen Sortiervorrichtung.
Eine Kugel verlässt im Punkt A ihre (waagerechte) Bahn mit der Horizontalgeschwindigkeit
v0 = 1 m/s und soll den im Punkt B positionierten
Behälter erreichen. An welcher Stelle x0 muss dieser Behälter stehen, wenn die
Höhendifferenz y0 = 1m beträgt?
Hinweis: Die Kugel beschreibt eine sog. Wurfparabel, die in Parameterdarstellung
folgende Gestalt besitzt: x=v0 t,
y= 0,5gt2
3
MST
Mathematik 2
Übung 6
Prof.Dr.B.Grabowski
(Anwendung komplexer Zahlen: LFZ von Polynomen und Schwingungen)
4