Übungsblatt 3

Mathematik 3
KI
Übung 3
Prof.Dr.B.Grabowski
(Schwingungen als komplexe Zeiger)
I. Darstellung von Schwingungen als komplexe Zeiger und ihre Überlagerung
Aufgabe 1
Eine harmonische (sinus-)Schwingung Asin (ωt + ϕ ) an der Stelle t kann als Imaginärteil der
komplexen Zahl z(t) = Ae j (ωt +ϕ ) aufgefasst werden.
D.h., jeder Schwingung Asin (ωt + ϕ ) kann man eindeutig die komplexe Zahl
z (t) = Ae j (ωt +ϕ ) = Ae jϕ ⋅ e jωt zuordnen. z(0)= Ae jϕ wird als komplexer Scheitelwert der
Schwingung bezeichnet.
Eine harmonische (sinus-)Schwingung Asin (ωx + ϕ ) wird in der Technik üblicherweise als
komplexer Zeiger z(0)= Ae jϕ dargestellt. ω charakterisiert, mit welcher Frequenz dieser
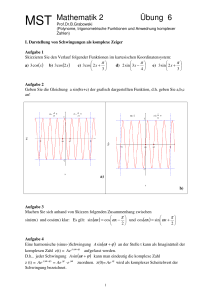
Zeiger im Koordinatensystem entgegengesetzt dem Urzeigersinn herumsaust. (siehe Skizze).
Darstellung der Schwingung
Asin (ωt + ϕ )
als komplexer Zeiger
a) Stellen Sie folgende Schwingungen als komplexe Zeiger dar ( ω=314 s-1)!
a1) u1(t) = 100V sin(ωt),
a2) u2(t) = 150Vcos(ωt - π/4)
(Hinweis: cosinus erst in den sinus umwandeln!)
b) Stellen Sie folgende komplexen Zeiger als Schwingungen dar!
b1) 2e
−j
π
4
,
ω=3
b2) 3e
j
π
3
, ω=2
Aufgabe 2
Bestimmen Sie die durch additive Überlagerung (Superposition) aus den beiden
gleichfrequenten Wechselspannungen y1(t) und y2(t) entstehende resultierende
Wechselspannung y(t) = y1(t) + y2(t) über die Methode der Komplexifizierung
(Sinustransformation) für ω=314 s-1!
y1(t) = 100V sin(ωt),
y2(t) = 150Vcos(ωt - π/4)
Zeichnen Sie y1(t), y2(t) und y(t) als komplexe Zeiger und verdeutlichen Sie sich damit
grafisch die Bedeutung der Rechenmethode !
1
Mathematik 3
KI
Übung 3
Prof.Dr.B.Grabowski
(Schwingungen als komplexe Zeiger)
Aufgabe 3
Zeigen Sie, dass gilt: a) cos(ϕ)=
II.
e jϕ + e − jϕ
2
b) sin(ϕ ) =
e jϕ − e − jϕ
2j
Wiederholung Integration
Aufgabe 4
Berechnen Sie alle Stammfunktionen von f(x)=x⋅sin(x) mittels Partieller Integration!
Aufgabe 5
Berechnen Sie mittels Partieller Integration und/oder geeigneter Substitution die folgenden 5
2π
und m und n beliebige Zahlen aus N0 = {0,1,2,3,...} sind:
Integrale, wobei ω =
T
T
T
a) ∫ sin(mwt ) sin(nwt )dt
b) ∫ cos(mwt ) cos(nwt )dt
0
o
T
d)
T
∫ cos(mwt )dt
0
c) ∫ cos(mwt ) sin(nwt )dt
0
T
e) ∫ sin(nwt )dt
0
2