Mathematik II Übung 2

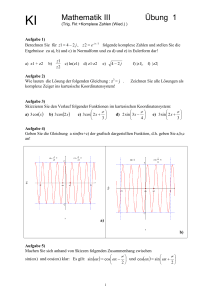
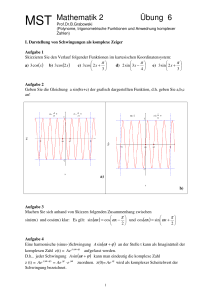
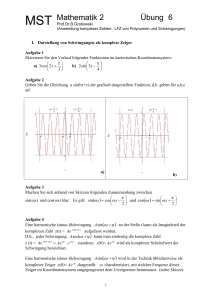
ASW
Mathematik II
Übung 2
(Komplexe Zahlen)
Aufgabe 1)
Wie lauten die Lösungen der folgenden Gleichungen ?
a)
z3 = j
b) z4 = 16 e j 160°
Zeichnen Sie alle Lösungen als komplexe Zeiger ins kartesische Koordinatensystem!
Aufgabe 2)
Berechnen Sie die folgenden Wurzeln:
a)
4−2j
b)
3
81e − j190°
Zeichnen Sie alle Lösungen als komplexe Zeiger ins kartesische Koordinatensystem!
Aufgabe 3)
Berechnen Sie die folgenden Logarithmen als komplexe Zahlen:
a) ln(1)
b) ln(-1+j)
Zeichnen Sie die Lösungen als komplexe Zeiger ins kartesische Koordinatensystem!
Aufgabe 4)
Bestimmen Sie sämtliche reellen und komplexen Lösungen der folgenden Gleichung :
x3 − x2 + 4x − 4 = 0
Aufgabe 5)
Zerlegen Sie das Polynom:
a) P(x) = 2 x 4 + 6 x 2 + 4
b) P(x) = 3 x 3 − 3 x 2 + 6 x − 6
in Linearfaktoren!
Aufgabe 6)
Skizzieren Sie den Verlauf folgender Funktionen im kartesischen Koordinatensystem:
π
π
π



a) 3 cos( x ) b) 3 cos(2 x )
c) 3 cos 2 x + 
d) 2 sin  3 x − 
e) 3 sin  2 x + 
3
4
3



Hinweis: Zeichnen von Acos(ωx + ϕ ) (Für Asin (ωx + ϕ ) bitte analog selbst überlegen)
• A ist die Amplitude, der Bereich ± A, in dem die Funktion schwankt, wird zunächst
ins Koordinatensystem eingetragen
• Nun wird für eine Schwingung der Funktion der Startpunkt xs bestimmt:
Dieser ist durch ϕ festgelegt und wird wie folgt für den cosinus bestimmt:
1
ASW
Mathematik II
Übung 2
(Komplexe Zahlen)
Es ist cos(u)= 1 ⇔ u = 0
d.h. cos(ωx + ϕ ) = 1 ⇔ ωx + ϕ = 0 ⇔ x s =
−ϕ
ω
2π
•
Durch die Kreisfrequenz ω ist die Periode T der Funktion festgelegt, es ist T =
•
Man trägt nun den Endpunkt xe = xs + T der einen Schwingung ein und zeichnet nun
die Schwingung. Am Anfang und am Ende ist der Wert der Schwingung = A, in der
Mitte = -A und dazwischen 0 (siehe Skizze, schwarz).
Nun kann die Schwingung periodisch fortgesetzt werden (pink)
ω
Aufgabe 7)
Machen Sie sich anhand von Skizzen folgenden Zusammenhang zwischen
π
π


sin(ωx) und cos(ωx) klar: Es gilt: sin (ωx ) = cos ωx −  und cos(ωx ) = sin  ωx + 
2
2


Aufgabe 8)
Eine harmonische (sinus-)Schwingung Asin (ωt + ϕ ) an der Stelle t kann als Imaginärteil der
komplexen Zahl z(t) = Ae j (ωt +ϕ ) aufgefasst werden.
D.h., jeder Schwingung Asin (ωt + ϕ ) kann man eindeutig die komplexe Zahl
z (t) = Ae j (ωt +ϕ ) = Ae jϕ ⋅ e jωt zuordnen. z(0)= Ae jϕ wird als komplexer Scheitelwert der
Schwingung bezeichnet.
Eine harmonische (sinus-)Schwingung Asin (ωx + ϕ ) wird in der Technik üblicherweise als
komplexer Zeiger z(0)= Ae jϕ dargestellt. ω charakterisiert, mit welcher Frequenz dieser
Zeiger im Koordinatensystem entgegengesetzt dem Urzeigersinn herumsaust. (siehe Skizze).
2
Mathematik II
ASW
Übung 2
(Komplexe Zahlen)
Darstellung der Schwingung
Asin (ωt + ϕ )
als komplexer Zeiger
a) Stellen Sie folgende Schwingungen als komplexe Zeiger dar ( ω=314 s-1)!
a1) u1(t) = 100V sin(ωt),
a2) u2(t) = 150Vcos(ωt - π/4)
(Hinweis: cosinus erst in den sinus umwandeln!)
b) Stellen Sie folgende komplexen Zeiger als Schwingungen dar!
b1) 2e
−j
π
4
, ω=3
b2) 3e
j
π
3
3
, ω=2