I. Natur des Lichts - BFH

Physik 1
Geometrische Optik 1
I. Natur des Lichts
Das Licht (und überhaupt alle elektromagnetische Strahlung, wovon das sichtbare Licht nur einen
kleinen Wellenlängenbereich abdeckt) gehört zu den wichtigsten und faszinierendsten Objekten
unserer Umwelt. Es wurde schon zu Newtons Zeiten intensiv untersucht, und schon aus dieser Zeit
stammt die Frage, ob es sich beim Licht um Teilchen handelt (dies war Newtons Meinung) oder um
Wellen (wie sein Zeitgenosse, der Holländer Huygens meinte).
Obwohl die beiden Meinungen sich nach der klassischen Physik gegenseitig ausschliessen, weiss
man aufgrund der Quantentheorie heute, dass alle elementaren Objekte gleichzeitig Teilchen- und
Welleneigenschaften haben. Dies gilt auch für das Licht.
Licht ist eine Form elektromagnetischer Strahlung (ebenso wie Radiowellen, Kurzwellen, Mikrowellen,
Infrarotstrahlung, UV-Strahlung, Röntgenstrahlen und die Gamma-Strahlen des radioaktiven Zerfalls).
Elektromagnetische Strahlen sind masselos (aufgrund der modernen Eichtheorien gibt es gute
Gründe dafür, dass die Masse streng = 0 sein muss) und transportieren keine elektrische Ladung. Im
Vakuum breiten sie sich mit der höchsten prinzipiell messbaren Geschwindigkeit aus, der
(Vakuum-)Lichtgeschwindigkeit
8
c0 = 299 792 458 m/s = 3⋅
⋅10 m/s
Licht als Welle:
Als Welle bezeichnet man die Ausbreitung einer ''Erregung''. Bei einer typischen Welle wird nicht
Materie transportiert, sondern Schwingungsenergie.
Licht zeigt die charakteristischen Eigenschaften
von Wellen: sie können sich "um die Ecke" ausbreiten
(''Beugung'') und bei Überlagerung von Wellen entsteht
"Interferenz ", d.h. Wellen verschiedener Phase können
sich ganz oder teilweise auslöschen.
Wellen sind charakterisiert durch die Frequenz
der Schwingung f und die Wellenlänge λ.
Beide Grössen hängen über die
Ausbreitungsgeschwindigkeit c zusammen:
c=fλ
(bei einer Schwingung wird eine Strecke λ
zurückgelegt; die benötigte Zeit für eine
Schwingung ist die Periode T = 1/ f, also ist
die Geschwindigkeit c = λ / T = λ f ).
Damit lässt sich bei bekanntem c für jede
Frequenz sofort die zugehörige Wellenlänge
ausrechnen.
Sichtbares
Licht
liegt
im
Wellenlängenbereich zwischen 380 nm
(violett) und 780 nm (rot).
Licht einer definierten Wellenlänge heisst
"monochromatisch" (einfarbig).
Oberhalb von 780 nm schliesst sich der
Infrarot (IR)-Bereich an, unterhalb von 380
nm der Ultraviolett (UV)-Bereich.
Das
Spektrum
(=Verteilung
verschiedene
Wellenlängen)
elektromagnetischen Wellen ist in
nebenstehenden Tabelle angegeben.
Stefan Stankowski
auf
der
der
BFH / HES BE HTI
Physik 1
Geometrische Optik 2
Licht als Teilchen ("Korpuskel", "Photon"):
Licht kann auch Teilcheneigenschaften zeigen, v.a. beim Stoss gegen andere Teilchen. Dies
geschieht z.B. beim Herausschlagen von Elektronen aus Metall beim "lichtelektrischen Effekt" in der
Fotozelle (ähnlich beim Photomultiplier; in der Photodiode werden die Ladungsträger in einen
beweglichen Zustand versetzt).
Ein Licht-Teilchen (Lichtquant, Photon) mit der Frequenz f besitzt nach der Quantentheorie die
Energie
E = hf = h ω
wo h die Plancksche Konstante ist: h = 6.625 10-34 Js. ( h = h / (2π) ).
Licht der Frequenz f kann Energie nur in Portionen (Quanten) der Grösse hf
transportieren.
Wellen- und Teilcheneigenschaften lassen sich
zum Teil unter einen Hut bringen mit der Vorstellung
von einem "Wellenpaket" endlicher Ausdehnung.
Geometrische Optik:
Falls man die Ausbreitung des Lichts unter Bedingungen betrachtet, wo alle interessierenden
geometrischen Abmessungen gross gegen die Wellenlänge sind, kann man davon ausgehen, dass
sich das Licht geradlinig in "Lichtstrahlen" ausbreitet (Beweis: Schatten). Für sichtbares Licht ist die
Bedingung der geometrischen Optik in den meisten Alltagsanwendungen gut erfüllt.
Vorsicht: im mikroskopischen Bereich sind Wellen-Effekte zu berücksichtigen!
Die im folgenden gezeigten Zusammenhänge gelten unter denselben Voraussetzungen im Prinzip
auch für andere Strahlung (andere elektromagnetische Wellen, Schall, radioaktive Strahlung usw.)
II. Ausbreitung des Lichts
Unter den Voraussetzungen der geometrischen Optik breitet sich das Licht im homogenen (überall
gleichartigen) Medium geradlinig mit konstanter Geschwindigkeit c aus.
8
Im Vakuum (in guter Näherung auch in Luft) beträgt die Lichtgeschwindigkeit ca. 3 ⋅ 10 m/s.
Sie ist unabhängig von der Wellenlänge (oder der Frequenz) und gilt ebenso auch für alle anderen
elektromagnetischen Strahlen.
Stefan Stankowski
BFH / HES BE HTI
Physik 1
Geometrische Optik 3
II.1 Eigenschaften des Ausbreitungsmediums
Brechungsindex
In anderen Medien als Vakuum (z.B. in Wasser, Glas ...) ist c verändert. (Dabei bleibt die Frequenz
gleich, die Wellenlänge ändert sich). Meist wird das Material nicht durch die Angabe von c
charakterisiert, sondern durch den
Brechungsindex n = c0 / c
(Vakuum-Lichtgeschw. / Lichtgeschw. im Medium)
Dispersion:
In diesen Materialien findet man ausserdem "Dispersion", das heisst, c hängt von der Wellenlänge
ab. Meistens liegt "normale Dispersion" vor, dann nimmt c umso mehr ab, je kleiner λ wird. Genau
genommen ist der oben definierte Brechungsindex also für alle Wellenlängen verschieden. Gibt man
den Brechungsindex für weisses Licht an, so ist ein mittlerer Wert gemeint.
II.2 Streuung
Enthält das Ausbreitungsmedium kleine Teilchen (Staub, Wassertröpfchen, Moleküle) so kann
Streuung auftreten: Das auf die Teilchen fallende Licht ändert seine Ausbreitungsrichtung.
(Eine genaue Analyse des Lichtanteils, der in verschiedene Raumrichtungen gestreut wird, kann
häufig Aufschluss über Grösse und Struktur der streuenden Teilchen geben. Dies ist ein wertvolles
Hilfsmittel der molekularen, atomaren und subatomaren Physik).
Die Wahrscheinlichkeit, dass das Licht überhaupt gestreut wird, nimmt stark mit der Frequenz des
Lichts zu; für gewöhnliche Streuung an kleinen Teilchen gilt:
Streu-Wahrscheinlichkeit ∼ f
4
(oder λ
-4
)
Dies ist der Grund für das Blau des Himmels
und den roten Sonnenuntergang!
II.3 Reflexion und Brechung
Beim Übertritt des Lichts von einem Medium zu einem anderem
Ausbreitungsgeschwindigkeit c treten in der Regel gleichzeitig zwei Effekte auf:
ein Teil des Lichts wird reflektiert (in das Ausgangsmedium zurückgestrahlt),
ein anderer Teil wird gebrochen (in das neue Medium hineingestrahlt).
Beide Vorgänge werden im folgenden näher untersucht, vor allem im
Hinblick auf ihre Eignung für optische Abbildungen.
Stefan Stankowski
mit
veränderter
BFH / HES BE HTI
Physik 1
Geometrische Optik 4
III. REFLEXION
Strahlrichtungen bezüglich einer Fläche werden durch den Winkel zum Einfalls-Lot angegeben.
III.1 Reflexionsgesetz:
Einfallender und reflektierter Strahl haben den gleichen Winkel zum Einfallslot.
III.2 Ebener Spiegel:
--> Das Spiegelbild liegt hinter dem Spiegel,
im gleichen Abstand wie das Objekt.
Virtuelles Bild:
Die Strahlen verlaufen so, als kämen sie aus
einem Bildpunkt, ohne dass sie tatsächlich dort
gewesen sind. Der extrapolierte Bildpunkt wird als
“virtuelles Bild“ bezeichnet.
Da unser Auge einfallende Strahlen so interpretiert,
als wären sie völlig geradlinig verlaufen, sieht es
einen scheinbaren Bildpunkt hinter dem Spiegel;
es wäre aber unmöglich, mit einer Mattscheibe
den Bildpunkt hinter dem Spiegel sichtbar zu machen.
Winkelspiegel:
Unabhängig vom Einfallswinkel wird ein (zweifach gespiegelter) Lichtstrahl um den Winkel δ = 2 γ ( abgelenkt.
Anwendungen bei der Vermessung und als Tripelspiegel
in Reflektoren.
Wichtige Anwendungen ebener Spiegel:
• Winkelmessung mit Drehspiegel
(Achtung: der Strahl wird um den
doppelten Winkel 2 α abgelenkt, wenn
sich der Spiegel um α dreht!)
• drehbarer Polygonspiegel zum Scannen
Gekrümmte Spiegel werden weiter unten im Zusammenhang
mit optischen Abbildungen behandelt.
Stefan Stankowski
BFH / HES BE HTI
Physik 1
Geometrische Optik 5
IV. Brechung
IV.1 Brechungsgesetz (Snellius)
sin α 1
= n 2 = c1
sin α 2
n1
c2
Dabei wird jedes Medium durch seinen
"Brechungsindex" n charakterisiert.
Je grösser n ist, desto grösser ist die
"optische Dichte" des Mediums.
Typische Werte von n (Mittelwert,
leichte Abweichungen je nach Wellenlänge!):
Vakuum:
Wasser:
Glas:
GaP (Halbleiter):
n=1
(Luft: n = 1.0003 , temperaturabhängig)
n = 1.33
n = 1.4 - 1.7 je nach Sorte, typisch: n= 1.5
n = 3.3
Der Brechungsindex ist umgekehrt proportional zur Ausbreitungsgeschwindigkeit im betreffenden
Medium i:
ni = c0 / ci
(c0 = Vakuum-Lichtgeschwindigkeit)
Das Brechungsgesetz lässt sich leicht erklären, wenn man
das Auftreffen eines Lichtbündels (ebene Wellenfront) an
einer Grenzfläche betrachtet, wo eine Seite des Bündels
die Fläche eher berührt und daher zuerst verlangsamt wird.
Prinzip von Fermat:
Das Licht wählt sich seinen Weg so, dass es dafür die
kürzest mögliche Zeit braucht.
Auch mit dieser Hypothese lässt sich das Brechungsgesetz
herleiten (wie auch das Reflexionsgesetz).
Optischer Weg:
Dies ist eine nützliche Grösse beim Studium der Lichtausbreitung.
Optischer Weg
= n mal tatsächlicher Weg
= äquivalenter Weg im Vakuum bei gleicher Laufzeit.
Brechungsindizes können auch
kontinuierlich ändern, z.B. in
Luftschichten mit Temperaturschichtung (Fata Morgana etc.)
Stefan Stankowski
BFH / HES BE HTI
Physik 1
Geometrische Optik 6
• Merkregel:
Beim Übergang zum dichteren Medium: Winkel zum Lot wird verkleinert
Beim Übergang zum dünneren Medium: Winkel zum Lot wird vergrössert.
IV.2 Totalreflexion
Beim Übergang des Lichts von einem dichteren zu einem dünneren Medium vergrössert sich der
o
Winkel zum Lot. Wenn der Austrittswinkel 90 erreicht, kann kein Licht mehr aus dem dichteren
Medium austreten. Es tritt dann Totalreflexion auf.
Der Grenzwinkel der Totalreflexion ergibt sich aus dem Brechungsgesetz mit der Bedingung sin α1 = 1
:
sin α lim = n1 / n2
Grenzwinkel der Totalreflexion
Bei Totalreflexion wird keine Lichtenergie durch das dünnere Medium fortgepflanzt.
Aufgrund der Wellennatur des Lichts ist allerdings trotzdem Licht in einer schmalen Grenzschicht
(Dicke von etwa einer Wellenlänge) des dünneren Mediums vorhanden (die sogenannte „evanescent
wave“). Dieser Grenzschicht-Effekt lässt sich für die Untersuchung mikroskopisch dünner Schichten
nutzen, z.B. wird der total reflektierte Strahl geschwächt, wenn an der Grenzschicht absorbierendes
Material angelagert wird: "Attenuated Total Reflection ATR").
IV.3 Lichtleiter
Die Totalreflexion wird technisch ausgenutzt, um Licht in optischen Fasern über grössere Strecken zu
leiten. Wegen der hohen Frequenz des Lichts ergeben sich hohe Uebertragungskapazitäten in der
Telekommunikation. Ausserdem sind Lichtleiter praktisch, um in schlecht zugängliche Hohlräume zu
schauen (technisch und medizinisch: Endoskopie).
Optische Fasern bestehen aus sehr reinem Siliciumoxid; Reste von Metall- und OH-Ionen sind neben
Streu-Effekten für die Lichtverluste verantwortlich.
Mit Beimischungen von Germaniumoxid erzielt man die nötigen Änderungen des Brechungsindexes.
Die wichtigsten Typen von Lichtleitern sind:
a) Stufenindex-Faser (Multimode)
Kern (typischer Durchmesser 0.1 mm) mit Brechungsindex n2, umgeben von Mantel mit
Brechungsindex n1 (geringfügig, z.B. 1%, kleiner als n2).
Der mögliche Einkoppelwinkel, bei dem noch Totalreflexion auftritt, wird als "numerische Apertur" NA
bezeichnet (in Analogie zum Einkoppelwinkel für Linsensysteme). Er liegt typischerweise in der
Grössenordnung von etwas über 10°.
_________
NA = n0 sin β ’ = √ n12 – n22
(β’ = max. Einstrahlwinkel, n1: Kern, n2: Mantel,
n0 = Brechungsindex Aussenmedium, meist =1, Luft)
Stefan Stankowski
BFH / HES BE HTI
Physik 1
Geometrische Optik 7
Strahlen mit verschiedenem Einfallswinkel innerhalb dieses Bereichs haben verschieden lange
Laufzeiten (sogenannte "Modendispersion"). Dies führt zur "Impulsverbreiterung" eines Signals.
Ein typischer Wert ist 50 ns pro km Faserlänge. Dadurch ist die erreichbare Bitrate für Impulsfolgen
limitiert.
b) Gradienten-Index-Faser (Multimode)
Hier variiert der Brechungsindex im Kern kontinuierlich zwischen einem Maximalwert in der Mitte und
einem Minimalwert am Rand. Der Verlauf der Lichtstrahlen ist nicht "eckig", sondern gebogen. Vorteil:
Weiter aussen verlaufende Strahlen mit grösserem Einkoppelwinkel haben zwar einen längeren Weg,
da auf ihrem Weg der Brechungsindex niedriger ist, sind sie aber auch schneller. Das heisst, der
optische Weg ist für die verschiedenen Laufwege sehr ähnlich und damit die Impulsverbreiterung
durch Modendispersion gering.
Wichtig wird in diesem Fall ein anderer Verbreiterungseffekt, die "Materialdispersion": Licht
verschiedener Wellenlänge hat leicht verschiedene Laufzeiten aufgrund des leicht veränderten
Brechungsindexes. Bei Einstrahlung mit einer LED erhält man eine Impulsverbreiterung von der
Ordnung 4 ns pro km, mit Lasereinstrahlung und sehr sauberem Brechzahlprofil bis zu 20 mal besser.
c) Monomode-Stufenindex
wie unter a), aber mit so kleinem Kern (Grössenordnung 5 µm), dass nur ein "Mode" (d.h. praktisch
nur der parallel zur Faser eingekoppelte Strahl) ausgebreitet werden kann.
Entscheidend für die Impulsverbreiterung ist auch hier die Materialdispersion. Bei Monomode-Fasern
kann sie unter günstigen Bedingungen durch einen weiteren Wellen-Effekt ("Wellenleiterdispersion")
kompensiert werden, die übertragbaren Bitraten werden dann sehr gross.
Nachteil der Monomodefasern: Verluste bei stärkerer Krümmung der Faser.
Lichtwellenleiter werden in Bündeln verlegt,
die aussen durch eine Hülle gegen mechanische
Belastung geschützt werden.
Stefan Stankowski
BFH / HES BE HTI
Physik 1
Geometrische Optik 8
V. Prisma
Ein Prisma ist ein (Glas-)Dreieck, das vor allem zu zwei grundverschiedenen Zwecken benutzt wird:
a) Strahlablenkung, z.B. im Prismenfernrohr, Kamerasucher etc.
(meist unter Ausnutzung der Totalreflexion)
b) Aufspaltung des Lichts in Komponenten verschiedener Wellenlänge (Farben) unter Ausnutzung der
Dispersion (Wellenlängen-Abhängigkeit des Brechungsindex).
Glasprismen zeigen "normale Dispersion", das heisst kurzwelliges Licht (blau) wird stärker gebrochen
als langwelliges Licht (rot).
Der Strahlablenkwinkel δ wird wesentlich durch den "brechenden Winkel " γ bestimmt:
γ = α = ε1 + ε2
δ + γ = ε1' + ε2'
sin εi'
------- = n
sin εi
(Aussenmedium Luft, n’ = 1)
Der Ablenkwinkel δ wird minimal bei symmetrischem Strahlendurchgang!
2ε’ = γ + δ
ε=γ/2
sin ½ (γ+δ) / sin ½ γ = n
Das Prisma war von grosser Bedeutung bei der Entwicklung der Spektroskopie
(= Untersuchung des Lichts auf seine Wellenlängen-Zusammensetzung).
Heute ist es in spektroskopischen Geräten durch Beugungsgitter ersetzt
(Licht-Aufspaltung durch Beugung: siehe Wellenoptik).
Stefan Stankowski
BFH / HES BE HTI
Physik 1
Geometrische Optik 9
VI. OPTISCHE ABBILDUNGEN
Lichtstrahlen haben immer die Tendenz auseinander zu laufen. Zu den wichtigsten Anwendungen
optischer Elemente gehört daher das Bündeln von Lichtstrahlen.
Werden Lichtstrahlen, die von einem leuchtenden Punkt ausgehen, wieder zu einem Punkt
zusammengeführt, so spricht man von einer Abbildung des Gegenstandspunkts in einen Bildpunkt.
Die wichtigsten optischen Elemente für optische Abbildungen sind gekrümmte Spiegel (Hohlspiegel,
Wölbspiegel) und gekrümmte Gläser (Linsen). Eine wichtige Rolle spielen zudem Blenden, mit denen
störende Randstrahlen ausgeblendet werden.
Im Prinzip kann man mit einer Blende allein bereits eine (allerdings sehr lichtschwache) Abbildung
erreichen (Lochkamera).
VI.1 Hohlspiegel (Konkavspiegel):
In der Praxis werden Hohlspiegel in der Regel als innen verspiegelte sphärische Kugelkalotte
hergestellt.
Radial durch den Mittelpunkt des Spiegels läuft die Hauptachse (optische Achse). Sie trifft den
Spiegel im "Scheitel" S.
Strahlen, die nahe der Hauptachse und unter kleinem Winkel zu dieser Achse verlaufen, heissen
"achsennah" oder "paraxial". Sie sind für die geometrische Optik von besonderer Bedeutung.
BRENNPUNKT:
Achsennahe Strahlen parallel zur Hauptachse werden so reflektiert, dass sie alle durch den
Brennpunkt F (Focus) verlaufen.
Ist R der Krümmungsradius des Spiegels,
so gilt für den Abstand f zwischen Brennpunkt F und Scheitelpunkt S:
Brennweite
f=½R
Abbildung am Hohlspiegel:
Ein Gegenstandspunkt G auf der Hauptachse, im "Gegenstandsabstand" g vom Scheitel, sende einen
Strahl unter kleinem Winkel αG zur Achse aus. Die Position B, wo der reflektierte Strahl die
Hauptachse schneidet, lässt sich leicht geometrisch aus dem Reflexionsgesetz konstruieren. Ihr
Abstand b vom Scheitel gehorcht der
Abbildungsgleichung (Descartes):
1
1
1
= +
f
g
b
Da diese Gleichung (für achsennahe Strahlen!) unabhängig vom Winkel αG ist, gilt sie für alle
(achsennahen) Strahlen aus dem Gegenstandspunkt. Dieser Punkt wird also in den Punkt B
abgebildet. Es handelt sich im Beispiel um ein reelles Bild, da die Strahlen dort tatsächlich hinkommen
(es kann mit einer Mattscheibe nachgewiesen werden).
Ebenso lässt sich geometrisch zeigen:
Stefan Stankowski
BFH / HES BE HTI
Physik 1
Geometrische Optik 10
Liegt der Gegenstandspunkt G ausserhalb der optischen Achse, so wird er in einen Bildpunkt B
abgebildet, der ebenfalls ausserhalb der optischen Achse liegt.
Die Abbildungsgleichung gilt genauso, wenn g und b weiterhin als auf die optische Achse projizierte
Abstände betrachtet werden.
Konstruktion des Bildpunkts:
Der Bildpunkt lässt sich leicht geometrisch konstruieren: es genügt, den Schnittpunkt von zwei der
folgenden Strahlen aus G zu bestimmen:
- Strahl durch Krümmungsmittelpunkt C: in sich selbst reflektiert
- Strahl durch F: parallel zur Hauptachse reflektiert
- Strahl parallel zur Hauptachse: durch F reflektiert
- Strahl zum Scheitel S: unter gleichem Winkel reflektiert
(Der Spiegel wird zweckmässig durch eine Ebene approximiert, um die achsennahen Strahlen zu
simulieren; die Konstruktion bleibt dann auch bei Benutzung grösserer Winkel korrekt)
Aus dieser Konstruktion folgt auch das Vergrösserungsverhältnis β für ausgedehnte Objekte.
Es wird so definiert, dass
β > 0: Bild aufrecht
β < 0: Bild invertiert (auf dem Kopf):
Abbildungsverhältnis:
Ausserdem ergibt sich sofort:
g > f : relles, invertiertes Bild
g = f : Bild im Unendlichen
g < f : virtuelles, aufrechtes
Spiegel
β = - b /g
Bild
hinter
dem
Merke: Virtuelle Abstände sind negativ!
Newton-Formel:
Statt auf den Scheitelpunkt kann man die Abstände auch auf den Brennpunkt beziehen:
z =g-f
z' = b - f
Dann schreibt sich die Abbildungsgleichung:
Stefan Stankowski
2
f = z z'
BFH / HES BE HTI
Physik 1
Geometrische Optik 11
VI.2 Parabolspiegel/ elliptischer Spiegel/ Zylinderspiegel:
Bei grosser Oeffnung des sphärischen Spiegels sind die Strahlen nicht mehr alle achsennah. Weiter
aussen liegende Strahlen werden dann nicht mehr im Brennpunkt gebündelt, sondern näher am
Scheitel ("Katakaustik").
Formt man den Hohlspiegel dagegen als Paraboloid, so treffen alle achsenparallelen Strahlen streng
in einem Punkt auf der Hauptachse zusammen, dem Brennpunkt der Parabel.
(Anwendung in der Astronomie, Satellitenkommunikation und für Reflektoren).
Beim elliptischen Spiegel wird ein Brennpunkt in den anderen abgebildet (Laser-Pumplampen).
Beim Zylinderspiegel wird ein Punkt auf eine Linie abgebildet.
VI.3 Wölbspiegel (Konvexspiegel):
Der sphärische Konvexspiegel besteht auf einer an der Aussenseite verspiegelten Kugelkalotte.
Die Abbildungsgesetze gelten genau gleich wie für den Hohlspiegel, wenn man verabredet,
dass Krümmungsradius und Brennweite, ebenso wie andere Distanzen hinter dem Spiegel als
negativ zu rechnen sind:
f<0
Das Bild ist, wie die geometrische Konstruktion zeigt, immer virtuell, aufrecht und verkleinert.
VI.4 Dünne Linse in Luft
Die Abbildungsgleichung für dünne Linsen in Luft
lässt sich z.B. herleiten, indem man die Linse als
eine Folge von Prismen mit zunehmendem (aber immer
kleinem) brechendem Winkel auffasst (siehe alternative.
Herleitung weiter unten, Matrixoptik).
In der symmetrischen Vorzeichenkonvention lautet die
Abbildungsgleichung für die dünne Linse in Luft:
1
1
1
= +
f
g
b
wobei die Brennweite f gegeben ist durch die
und den Brechungsindex des Linsenmaterials:
Krümmungsradien der Linsenseiten
1
1 1
= (n-1) ( - )
f
r1 r2
Stefan Stankowski
BFH / HES BE HTI
Physik 1
Geometrische Optik 12
Aus der Bildkonstruktion (siehe unten) folgt, ebenfalls analog zum Hohlspiegel:
β =-
b
g
Beachte: Die Linse hat zwei Brennpunkte, die beide gleich weit von der Linsenmitte entfernt sind, auch
wenn die zwei Linsenseiten nicht gleich sind!
Bildkonstruktion
Für die Bildkonstruktion wird die Linse durch ihre "Hauptebene" repräsentiert.
Es bieten sich zwei der folgenden Strahlen an:
- Strahl durch Brennpunkt: geht parallel zur Hauptachse weiter
- Strahl parallel zur Hauptachse: verläuft durch Brennpunkt
- Strahl durch Linsenmitte: verläuft geradlinig weiter
Unter Ausnutzung der Abbildungsgleichung ergibt sich die folgende nützliche Konstruktion des
gebrochenen Strahls bei beliebigem Einfallswinkel:
parallelen Strahl durch Linsenmitte zeichnen;
der gebrochene Strahl schneidet diesen in der
Brenn-Ebene.
Optiker benutzen gern die Brechkraft (englisch: power) einer
Linse:
Brechkraft B = 1/f gemessen in Dioptrien = 1/m
Die wichtigsten Linsentypen:
Konvexe Krümmung erzeugt einen Sammeleffekt (konvergente Linse);
konkave Krümmung erzeugt einen Zerstreuungseffekt (divergente Linse).
Konvex-konkave Linsen sind sammelnd, wenn die konvexe Seite stärker gekrümmt ist, zerstreuend,
wenn die konkave Seite stärker gekrümmt ist.
Konkave Krümmung: der entsprechende Krümmungsradius ist negativ zu nehmen!
Demnach wird bei der Zerstreuungslinse die Brennweite negativ!
Sonst können alle Gleichungen für die Zerstreuungslinse beibehalten werden.
Stefan Stankowski
BFH / HES BE HTI
Physik 1
Geometrische Optik 13
Aus der geometrischen Konstruktion ergibt sich für die Sammel-Linse:
g > 2f
Bild reell, invertiert, verkleinert
g = 2f
Bild reell, invertiert, 1:1
2f > g >f
Bild reell, invertiert, vergrössert
g=f
Bild im Unendlichen
g<f
Bild virtuell, aufrecht, vergrössert
Bildkonstruktion für die Zerstreuungslinse:
beachte, dass die Brennpunkte ihre Rolle vertauschen.
Das Bild ist immer virtuell, aufrecht und verkleinert.
Vorzeichenkonvention:
Die hier verwendeten Vorzeichen sind positiv für alle Distanzen zu reellen Punkten, negativ bei
virtuellen Punkten.
Krümmungsradien sind positiv, wenn die Linsenseite zur Einfallsseite des Strahls hin gewölbt ist,
negativ, wenn sie vom Strahl weg gekrümmt ist.
Brennweiten sind positiv für sammelnde, negativ für zerstreuende Linsen.
VI.5 Dünne Linse mit verschiedenen Medien auf beiden Seiten
Die Brennweiten in den beiden Medien sind nun
nicht mehr gleich. Die Abbildungsgleichungen
lauten:
n- n1 n- n 2
= n1 + n 2
g b
r1
r2
b
β = - n1
n2 g
wo g und b >0 sind für reelle und <0 für virtuelle
Punkte (symmetrische Vorzeichenkonvention).
n = Brechungsindex des Linsenmaterials.
VI.6 Sphärisch gekrümmte Begrenzung zwischen zwei Medien
Gegeben sei eine sphärisch gekrümmte Begrenzung,
links davon Medium 1, rechts davon Medium 2. Für
achsennahe Strahlen gilt dann
die Abbildungsbedingung
n 2 − n1 = n1 + n 2
r
g b
b
β = − n1
n2 g
immer mit der gleichen Vorzeichenkonvention:
r ist positiv zu rechnen, wenn die Grenzfläche
zum Medium 1 hin konvex gekrümmt ist.
Stefan Stankowski
BFH / HES BE HTI
Physik 1
Geometrische Optik 14
VII. Linsensysteme
VII.1 Linsen in engem Kontakt
Sind zwei Linsen in Berührung miteinander, sodass ihr gegenseitiger Abstand klein gegen die übrigen
Distanzen (Brennweite, Gegenstandsweite etc.) ist, und kann die kombinierte Linse immer noch als dünn
aufgefasst werden, so ist die Brechkraft additiv:
1
1
1
+
=
f
f1 f 2
Wie bei der einzelnen dünnen Linse liegt die "Hauptebene" (= Bezugsebene für die Konstruktion der
Abbildungsstrahlen) am Ort der kombinierten Linse.
VII.2 Beliebige Linsensysteme
Sie lassen sich konstruktiv und rechnerisch mit den bereits behandelten Methoden bewältigen.
Regel: auf eine Linse auffallender divergenter (auseinanderlaufender) Strahl:
reeller Gegenstand (g>0);
auf eine Linse auffallender konvergenter (zusammenlaufender) Strahl:
virtueller Gegenstand (g<0).
Rechnerische schrittweise Lösung:
Gegeben seien die Brennweiten f1, f2 der Linsen, ihr Abstand d und die Gegenstandsweite g1 vor der
ersten Linse. Dann berechnet sich das Zwischenbild aus der Abbildungsgleichung:
1
1 1
=
b1 f 1 g1
Das Zwischenbild wird Gegenstand für die Abbildung an der zweiten Linse:
g2 = d - b1
Schliesslich ergibt sich die Bildweite hinter der zweiten Linse, b2, aus:
1
1
1
=
b2
f 2 g2
Der Abbildungsmasstab ist:
β = β 1 β 2 = (- b1 )(- b2 )
g1
g2
Konstruktiv lässt sich zuerst das Zwischenbild ermitteln und von dort ausgehend das Bild. Im Fall, wo g2
< 0 wird, ist dieses Verfahren aber mühsam und verursacht leicht Fehler. Zu empfehlen ist daher, direkt
den Strahlengang von Linse zu Linse zu verfolgen, wobei die Brechung beliebiger Strahlen auf einer
Linse mittels parallelem Hilfsstrahl durch die Linsenmitte zu konstruieren ist (der den zu findenden Strahl
in der Brennebene trifft).
Konstruktionsbeispiel mit
Sammel- und
Zerstreuungslinse:
Stefan Stankowski
BFH / HES BE HTI
Physik 1
Geometrische Optik 15
Eine andere, sehr elegante Methode benutzt zur Darstellung des Strahls Matrizen; diese Matrix-Optik
wird im Anhang dargestellt. Damit wird auch die Berechnung dicker Linsen möglich.
Nur erwähnt wird im folgenden die Darstellung eines Zwei-Linsen-Systems mittels Hauptebenen:
Hauptebenen:
Linsensysteme lassen sich durch die Angabe von zwei Hauptebenen charakterisieren, eine
gegenstandsseitige Hauptebene H und eine bildseitige Hauptebene H'.
Der Brennpunkt F' ist das Bild eines unendlich fernen Gegenstands und gehört zur Hauptebene H';
der Brennpunkt F ist Gegenstandspunkt für ein unendlich fernes Bild und gehört zur Hauptebene H.
F'H' = FH = System-Brennweite f.
Die Konstruktion ist im folgenden Schema ersichtlich (beachte die parallele Versetzung des Strahls
zur Linsenmitte):
Position der Hauptebenen für ein System aus zwei dünnen Linsen L1, L2 im Abstand d:
L1 H =
df
df
1
1
1
d
; L2 H ′ =
;
=
+
−
f
f1
f2
f1 f2 f1f2
dabei ist LH positiv, wenn es zur Mitte zwischen
den zwei Linsen zeigt, sonst negativ.
VIII. Dicke Linse
Auch hier ergeben sich zwei Hauptebenen. Mit der Linsendicke (Scheitel-Scheitel-Abstand) d:
SH = f
2
n −1 d
n −1 d
1
1 1
(n − 1) d
; S ′H ′ = f
;
= (n − 1)( − ) +
n r2
n r1 f
n r1 r 2
r1 r 2
Wieder ist SH positiv, wenn es zum Linsenzentrum zeigt, negativ, wenn es nach aussen zeigt.
Beachte: Die zwei Hauptebenen können "gekreuzt" stehen, sodass H näher am Scheitel S' und H'
näher am Scheitel S steht. Die Hauptebenen können auch ausserhalb der Linse liegen.
Stefan Stankowski
BFH / HES BE HTI
Physik 1
Geometrische Optik 16
IX. Linsenfehler:
- Sphärische Aberration:
Randstrahlen-Effekt.
Korrektur: Randstrahlen ausblenden, Kombination von Linsen mit
verschiedenem Brechungsindex.
- Astigmatismus:
Mangelnde Achsennähe sehr schief auftreffender Strahlen.
Korrektur: Linsenkombinationen.
- Chromatische Aberration:
Farbabhängigkeit der Brechkraft.
Korrektur:
Linsenkombinationen
mit
verschiedenen
Brechungsindizes.
X. Optische Systeme, Auflösungsvermögen
Je nach verfügbarer Zeit werden im Kurs einige optische Systeme vorgestellt (Lupe, Fernrohr,
Mikroskop etc.). Beachten Sie in jedem Fall, dass es nicht nur auf die erreichbare Vergrösserung
ankommt, sondern auch auf das
Auflösungsvermögen = Fähigkeit, zwei nahe Punkte noch getrennt wiederzugeben.
Aus der Wellenoptik (Beugung) folgt, dass zwei Punkte, die unter dem Winkel α erscheinen, noch als
getrennte Punkte wiedergegeben werden, wenn
α > 1.22 λ / d
(d = Blendendurchmesser)
Je kleiner die Wellenlänge, desto besser wird also die Auflösung.
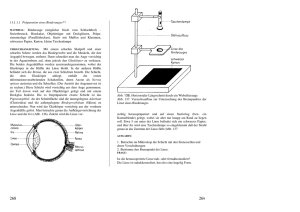
Erheblich kleinere Wellenlängen als mit sichtbarem
Licht erreicht man z.B. mit hoch beschleunigten Elektronen
(die nach der Quantentheorie auch als Welle aufgefasst
werden können): Elektronenmikroskop.
Der Elektronenstrahl wird durch Magnetlinsen gebündelt
und durchstrahlt die Probe (Transmissions-EM) oder
tastet sie in der Reflexion ab (Raster-EM).
Die Probe muss im Vakuum eingeführt werden.
Stefan Stankowski
BFH / HES BE HTI