geometrische optik

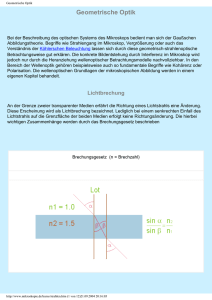
Kapitel 16
GEOMETRISCHE OPTIK
Die geometrische Optik ist die
erste Näherung zur Wahrheit.
Lichtrahlen werden definiert
, -& + %. / 0
als dünne Bündel von Licht,
1 # 2 $ & %*3 4 5 &
die sich in isotropen Medien
6 & --& $ / ) %*+
geradlinig ausbreiten, normal
zur Phasenfläche. Anschaulich,
2 & / 1 & %. *3 4 5 &
aber auf Grund von Beugungs( ) %*+
effekten nicht richtig für den
Rand der Lichtbündel.
Die G.O. ist eine gute Näherung, solange das Strahlbündel groß ist gegen λ.
Man ordnet dem Lichtstrahl bestimmte Welleneigenschaften zu (Wellenlänge,
Phasengeschwindigkeit, Intensität, Polarisation, . . . ) und verwendet die
! " # $ %& $ '( ) %*+
Postulate der geometrischen Optik:
• Lichtstrahlen verlaufen in einem homogenen Medium als Gerade.
• Das Medium ist durch den reellen Brechungsindex n ≥ 1 charakterisiert. Die Laufzeit für die Strecke d ist d n/c.
Das Produkt d n bezeichnet man als die optische Weglänge.
!B
• in einem inhomogenen Medium ist die optische Weglänge A n("r)ds.
• Das Prinzip von Fermat gilt für Strahlen die von Punkt A nach Punkt B
laufen: Die Laufzeit ist ein Minimum d.h. die Variation der optischen
Weglänge ist Null
δ
"
B
n("r) ds = 0
(16.1)
A
• Daraus folgt, dass an Grenzflächen die Strahlen dem Brechungsgesetz von
Snellius folgen bzw. dass Einfallswinkel und Ausfallswinkel gleich sind.
Überkreuzende Strahlenbündel beeinflussen sich nicht1 .
1 Interferenz
ist Teil der Wellenoptik.
141
142
KAPITEL 16. GEOMETRISCHE OPTIK
Ausbreitung in homogenen Medien:
im homogenen durchsichtigen Medium
läuft Licht entlang von geraden Linien.
! "# $% &&' ( ) ( # (
Reflexion an Spiegeloberflächen:
”reflektierter Strahl liegt in der
Einfallsebene,
Reflexionswinkel = Einfallswinkel
* + , - % &(
!
!
. / "( 0 ( &1
+ ) ( , $&2 3 4 (
! " # $ % &'
Reflexion und Brechung:
gebrochener Strahl in der Einfallsebene
Snellius gilt: n sin ϕ =const.
!
!
16.1
Optische Abbildung mit Reflexion
mit Spiegel
mit Lochkamera
! "
d! =
a+b
d
a
$
#
!
"
# %
143
16.1. OPTISCHE ABBILDUNG MIT REFLEXION
ebener Spiegel
elliptischer Spiegel
!
! "
! "
!
sphärischer Spiegel
parabolischer Spiegel
x2 + y 2 = R2
y 2 = 2px
!
!
"
#
Paraxialstrahlen (achsennahe) im sphärischen Hohlspiegel
Für kleine Winkel ϕ gilt ϕ1 + ϕ2 = 2 ϕ0 , wobei ϕ0 ≈ tan ϕ0 = y/R
!
!
'
!
#
!
*
%
In dieser Näherung ist die
Brennweite des Spiegels
"
"
"
)
#
$
"
(
%
1
1
2
+
≈
z1
z2
R
&
'
f=
R
2
'
Abbildung mit konkavem sphärischen Spiegel (Paraxialnäherung)
144
KAPITEL 16. GEOMETRISCHE OPTIK
#
!
$
%& $ '( $ )
"
!
"
*
#
+
%& + '( + )
Reelle bzw. virtuelle Bilder.
!
Abbildungsmaßstab:
"
y2 /y1 = −z2 /z1
16.2
#
!
Ebene Grenzflächen
n1
<
n2
n1
> n2
ϕ1
> ϕ2
ϕ1
< ϕ2
#
!
"
!
!
"
!
#
"
!
Für Paraxialstrahlen gilt die Näherung n1 ϕ1 ≈ n2 ϕ2 . Für n2 < n1 tritt Totalreflexion auf, wenn ϕ2 → 90o . Der Grenzwinkel für Totalreflexion ist sin ϕg =
n2 /n1 .
Prisma
Blaues Licht wird stärker gebrochen als rotes, wenn normale Dispersion vorliegt
(dn/dλ < 0) und das Prisma ein Medium mit höherem Index ist als die Umgebung ist (z.B. konventionelles Glasprisma in Luft).
Die kleinste Ablenkung erfolgt bei symmetrischem Strahlengang α1 = α2 .
145
16.3. SPHÄRISCHE GRENZFLÄCHEN
δmin = 2α − γ
δ = α1 + α2 − γ
!
!
# "
#
"
"
"
!
!
$ +, +( $ ' +, +* ."
# $
"
!
% &'
! "
# $
Die Effizienz von Strahlteilern wird
durch den Brechungsindexsprung an
den Grenzflächen, bzw. über optische
Beschichtung mit λ/4 bzw. λ/2 Schichten bestimmt. Die Effizient hängt im
allgemeinen stark von der Wellenlänge
und vom Polarisationszustand (s oder
p ab.
16.3
) $
( $
#
! "
! "
# $ % &'( ))
! "
Sphärische Grenzflächen
werden auf Grund der einfachen Herstellung oft für Spiegel, Linsen verwendet.
Für paraxiale Strahlen ist das Gesetz
von Snellius näherungsweise gleich
!
"
n1 α ≈ n2 β
# $ %!
In dieser Näherung ist die Brennweite
n2
f2 = R
n2 − n1
!
"
&
#
&
$ %)
*"
'
(
' "+ '
(
Für dünne Linsen ist der
Abstand zwischen den Grenzflächen klein gegen die Brennweite. (im Beispiel: bikonvex mit
gleichen
Krümmungsradien).
Die Abbildungsgleichung ist
1 1
1
+ =
g
b
f
Linsentypen
*
'
+
!" # $% # &
(
!" , $% , &
! )*
146
KAPITEL 16. GEOMETRISCHE OPTIK
! "#
$ % & ' ( )
* +, & #
$ % & ' ( )
$ % & ' ( ) #
$ % & $ , '
! "#
$ % & $ , '
* +, & #
$ % & $ , '
, - * . / 0 "- 1 .
Für dicke Linsen führt man Hauptebenen ein. An diesen verhalten sich einfallende Strahlen wie in der Näherung für dünne Linsen.
"
"
#
$
&
#
&
$
!
!
"
!
$
%
$
%
#
16.4
#
$
%
&
Linsenfehler
Die chromatische Abberation (Ort
des Fokus ist wegen der Dispersion
für unterschiedliche Farbe verschieden)
kann durch Achromate verhindert
werden.
Mit sphärischer Abberation bezeichnet man den Umstand, dass der
Ort des Fokus wegen der Kugeloberfläche für achsenferne Strahlen anders
liegt als für achsennahe.
!
!
!
" # $ # % &# '
#& '
" #$ %
!
$# ( )
!
%
(
%
)
* + , #& - . '
Auf Grund des Astigmatismus werden Gegenstandspunkte, die weit von der
Achse liegen, verzerrt abgebildet. Die einfallenden Strahlen sehen sagittal bzw.
147
16.5. LICHTLEITER
meridional andere Krümmungsradien und werden an unterschiedlichen Brennpunkten fokussiert. Der Einfluß ist umso größer, je schiefer das Lichtbündel
einfällt.
"
#
!
$
$
!
"
!
Bildfeldwölbung
"
16.5
Lichtleiter
funktionieren mit Linsen oder Spiegeln, aber mit geringsten Verlusten unter
Verwendung von Glasfasern. Diese nutzen die Totalreflektion aus.
!
"
!
#
Die numerische Apertur einer optischen Faser beschreibt den maximalen
Winkel unter dem ein Lichtstrahl in eine Faser eintreten kann, um der Totalreflexion zu unterliegen:
N A = sin θa =
#
n21 − n22
Typisch für Glasfasern sind Werte n1 = 1.475 und n2 = 1.460. Daraus folgt ein
Wert von N A = 0.2, bzw. θa = 12o .
"
#
"
*
!
!
( ' )"
$ % &&'
In Graded-Index Optiken (GRIN) liegt eine kontinuierliche Variation von
n(r) vor. Damit folgen die Lichtstrahlen gekrümmten Trajektorien.
148
KAPITEL 16. GEOMETRISCHE OPTIK
!
!
% &! "# "! ! '
! "# "! !
%
!
$
!
%
!
!
$
16.6
%
Geometrische Optik der Erdatmosphäre
• Scheinbare Sternposition: Da die atmosphärische Dichte ρ mit der
Höhe abnimmt, und in guter Näherung n − 1 ∝ ρ = ρ0 exp(−r/8.3km)
ist, verhält sich die Atmospäre wie ein GRIN Medium. Der Fehler in der
Position des Sternes nimmt mit dem Winkel vom Zenith zu.
• Erweiterung der Sichtweite: ebenfalls auf Grund der Dichteabnahme
mit der Höhe über dem Erdboden.
• Fata Morgana: Auf Grund starker Temperaturgradienten in Bodennähe
wird der Strahlengang verkrümmt und das gesehene Objekt erscheint an
anderer Stelle. Da Wellenfronten Punkte gleicher Phase verbinden und der
Ausbreitungsvektor senkrecht auf die Wellenfront liegt, kann man folgenden Ansatz für den Krümmungsradius der Lichtbahn machen:
( * !
+,- .
% * !
' ( )
$ % "
$ &
! "# $ %& %' ( $ )
$ %
#
!
"
!
#
&
* "+ ,! - .%,"& %,"/ ,0 1 2 + / / 3 $ + ,4 3 ' 5 + '
$ !
Eine Bahn verläuft in einem Bereich mit Brechungsindex n über eine
Wegstrecke r dϕ. Ein benachbarter Bereich hat den Brechungsindex n +
dn
dr dr. Diese Bahn durchquert zwischen zwei Phasenflächen die geometrische Strecke (r + dr) dϕ. Da zwischen benachbarten Phasenflächen die
optischen Wegstrecken gleich sind, muss gelten:
n r dϕ = (n +
dn
dr) · (r + dr) dϕ
dr
In der Näherung, dass der Term mit dr2 vernachlässigbar ist, ergibt sich
für den Krümmungsradius
r=
n
dn/dr
(16.2)
149
16.6. GEOMETRISCHE OPTIK DER ERDATMOSPHÄRE
im homogenen Fall wird also der Radius ∞.
• Regenbogen: Beim Durchgang eines Lichtstrahls durch ein Wassertröpfchen in der Nähe des geometrischen Zentrums kommt es zu einer
geringen Stahlablenkung. In diesem Bereich wird Licht im wesentlichen in
Vorwärtsrichtung gestreut. Mit steigendem Abstand vom Zentrum erhöht
sich die Ablenkung und gleichzeitig steigt der beim Austritt ins Tröpchen
zurückreflektierte Anteil der Strahlung. Strahlen, die nach einmaliger Reflexion aus dem Tröpchen austreten, konzentrieren sich im wesentlichen
um Ablenkwinkel von 180o − 42o , nach zweimaliger Reflexion (und auf
Grund des zusätzlichen Reflexionsverlustes schwächer) um Ablenkwinkel
von 180o − 51o . Der exakte Winkel hängt auf Grund der Dispersion des
Wassers von der Farbe ab. Unter diesen Winkeln sehen wir (vorausgesetzt
die Sonne steht hinter uns) zwei Regenbögen. Die Dispersion erscheint in
den beiden Bögen entgegengesetzt, innen rot. Eine genauere Behandlung
(Airy 1838) zeigt, dass in die Erscheinung des Regenbogens auf Grund
von Beugung die Größe des Tröpchens eingeht und die Interferenz der
austretenden Strahlen berücksichtigt werden muss.
#
!
( ) * * + * , -./ 0 1
2
"
( ) * * + * , -./ 0 1
"
!
#
$ % &
$ % &
$ ' &
$ ' &
Caustics
Caustic
42o
Im Bild links ist die Intensität jedes einzelnen
gebrochenen Strahles als
gleich angenommen. In
Wirklichkeit betonen die
Fresnelschen Bedingungen
(siehe Seite 131) die Konzentration von intensiven
Strahlen in den Ablenkbereich von 40-420 noch
stärker, als es bereits
durch die Kaustik geschieht.