Ausgewählte Kapitel der Physik

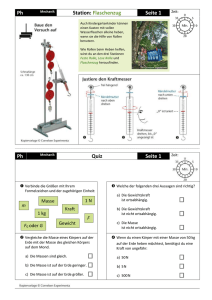
Ausgewählte Kapitel der Physik
Mechanik
Lehre von den Kräften = Dynamik
13.04.2015
Mechanik
• Dynamik: Kraft und Masse
• Newtonsche Axiome
Eine Kraft beeinflusst einen Körper
insofern sie seinen Bewegungszustand ändert,
und / oder ihn deformiert.
Nur durch diese Wirkung wird Kraft erkennbar.
Fundamentale Kräfte sind die Gravitationskraft, die
elektrische- und die magnetische Kraft.
Unter „Masse“ verstehen wir zwei verschiedene
Erscheinungsformen desselben Körpers, und zwar:
Die Schwere = Graviation = Massenanziehung
Die Trägheit = Widerstand gegen Änderungen des
Bewegungszustands.
[Träge Masse] = [schwere Masse] = 1kg (Paris)
13.04.2015
Die Newtonschen Axiome verknüpfen die
Bewegungen mit den sie verursachenden
Kräften.
Mechanik
• Erstes Axiom von Sir Isaak Newton
Das Trägheitsprinzip besagt:
Ein Körper verharrt im Zustand der
Ruhe oder der gleichförmigen
geradlinigen Bewegung, solange
keine äußeren Kräfte auf ihn
wirken.
13.04.2015
Die Ursache jeder
Bewegungszustands-Änderung
ist das Wirken von Kräften.
Mechanik
• Zweites Axiom von Sir Isaak Newton
Die wirkende Kraft und die erzielte Beschleunigung
sind zueinander proportional
1N ist die Kraft, die der Masse
1 kg die Beschleunigung 1 m/s² erteilt.
F=~ a
Die Proportionalitäts-konstante ist die Masse
F=m*a
[F] =1kg*1m/s² =1Newton
13.04.2015
Wenn eine Bewegungsänderung
beobachtet wird,
dann steckt eine Kraft dahinter!
Mechanik
• Zweites Axiom von Sir Isaak Newton
Auf jeden Körper wirkt die Schwerkraft der Erde bzw.
anderer (Himmels-) Körper. Die Masse ist schwer, lat.:
„gravis“ . Die Gravitation des einen Körpers wirkt auf eine
andere schwere Masse anziehend. Und umgekehrt. (Ob es
eine abstoßende Gravitation gibt, wir derzeit untersucht)
Unter der Gewichtskraft versteht man die Kraft, die auf ihn
im Schwerefeld einer großen Masse wirkt.
Diese Kraft bewirkt ebenfalls eine beschleunigte
Bewegung (wenn man die Probe nicht zurückhält)
Die Gewichtskraft (=Gewicht) ergibt sich zu:
G = m*g
m= Masse in kg
G = m * 9,81 m/s²
Erdbescheunigung auf Meeresniveau
Äquator:
g=9,780 m/s²
45° n. Breite
g=9,806 m/s²
Pol:
g=9,832 m/s²
13.04.2015
1N ist die Kraft, die der Masse
1 kg die Beschleunigung 1 m/s² erteilt.
Wenn eine Bewegungsänderung
beobachtet wird,
dann steckt eine Kraft dahinter!
Mechanik
• Drittes Axiom von Sir Isaak Newton
Das Reaktions- oder Wechselwirkungsprinzip:
Jede Kraft besitzt eine Gegenkraft von gleichem Betrag aber entgegengesetzter Richtung.
Die Angriffspunkte der Kräfte liegen in zwei verschiedenen Körpern.
Beispiele: Gravitationskraft, Kräfte zwischen zwei Magneten, elektrische Kräfte zw. Geladenen Körpern,
Kernkräfte, Kräfte bei elastischen Verformungen, Kräfte zwischen Molekülen,…
Wenn zwei Kräfte an einem Körper angreifen, sind dies nicht Reaktionskräfte im Sinne des 3. Axioms.
Diese können sich kompensieren oder auch ein Drehmoment erzeugen.
13.04.2015
Mechanik
• Dynamik der Drehbewegung
Wenn sich eine Punktmasse (oder ein
Massepunkt eines starren Körpers) auf einer
Kreisbahn bewegt, so ist ständig eine zum
Mittelpunkt gerichtete (= zentrale) Beschleunigung
wirksam. Die Kreisbewegung verlangt daher eine
zum Rotationszentrum gerichtete Kraft, die
Zentripetalkraft. Es gilt wie bei der Translation:
F = m*ar
Die Zentralbeschleunigung ar hängt mit der
Bahngeschwindigkeit der Umdrehung zusammen:
ar = v²/r = w² * r
Fr = m*ar = m*v²/r =m*w² *r
Die nach Außen wirkende Gegenkraft Fz ist gleich
groß!
Fr = -Fz
13.04.2015
Die Corioliskraft ist eine Kraft die auftritt, wenn
man sich auf der rotierenden Scheibe mit v
nach Außen oder Innen bewegt.
Mechanik
• Dynamik der Drehbewegung
Die Formel:
Fr = m*ar (= -Fz )
beschreibt die Zentralkraft bei der Rotation. Mit dieser Kraft wird
ein Masseteilchen auf der Kreisbahn zurückgehalten. (Sonst würde
es tangential wegfliegen).
Eine Tangetialkraft ist notwendig, wenn man die Scheibe in
Rotation versetzen möchte, bzw. wenn die Winkelgeschwindigkeit
geändert werden soll:
Ft ~ a
Für den Antrieb ist auch entscheidend, in welchem Abstand von
der Drehachse die Kraft angreift, wie groß also das
Drehmoment M = Ft * r (Kraft mal Hebelarm) ist:
M~a
Die Trägheit gegenüber der Bewegungsänderung hängt nicht bloß
von der Masse ab, sondern auch von deren Verteilung J im
Hinblick auf die Drehachse:
M=J*a
Der Proportionalitätsfaktor J heißt Massenträgheitsmoment
13.04.2015
Das Massenträgheitsmoment berechnet
man aus Radius ri² mal Masse Dmi
aufsummiert über alle Punkte des Körpers.
J   r 2 dm
Diese Integrale sind für zahlreiche
Geometrien schon berechnet und tabelliert
Mechanik
• Massenträgheitsmoment
Eine (punktförmige) Masse auf einer Kreisbahn hat das Trägheitsmoment : J = m*r²
z.B. m=100g, r=1,5m J= m.r² = 0,225 kg.m²
Ein Ring besteht aus hintereinander gereihten Massenpunkten im gleichen Abstand r vom Drehpunkt. Damit
wird J= r² Sm
z.B. m=0,5Kg, r=30cm, J=0,3².0,5 kg.m²=0,045kg.m²
Bei einer Scheibe muss richtig integriert werden. Die inneren Massen tragen wegen des Quadrats von r
weniger zum Trägheitsmoment bei als gleiche Massen weiter außen.
z.B. Eine Scheibe mit Masse 2kg und Durchmesser 20cm; J= ½ M*R² = ½ 2kg.(0,1m)² = 0.01kgm²
Herleitung der Formel für axiale Zylinder aus: J   ri 2 .dm
Volumenselement: dm   * dV   * h * db * dr   * h * r.d * dr
R 2
4
2
R
R
J   * h   r * r.d * dr   * h *2
  *V *
 12 M * R 2
4
2
0 0
2
13.04.2015
Mechanik
• Massenträgheitsmoment - Drehachsen
Bei Kenntnis des Trägheitsmoments Js um eine Drehachse durch den
Schwerpunkt lässt sich das Trägheitsmoment um eine um den Abstand s
parallel verschobene Drehachse mit dem Satz von Steiner berechnen.
J = Js + m.s²
13.04.2015
Mechanik
13.04.2015