Quanten Entstehu a) Intens b) Photo Beobach - O - - W

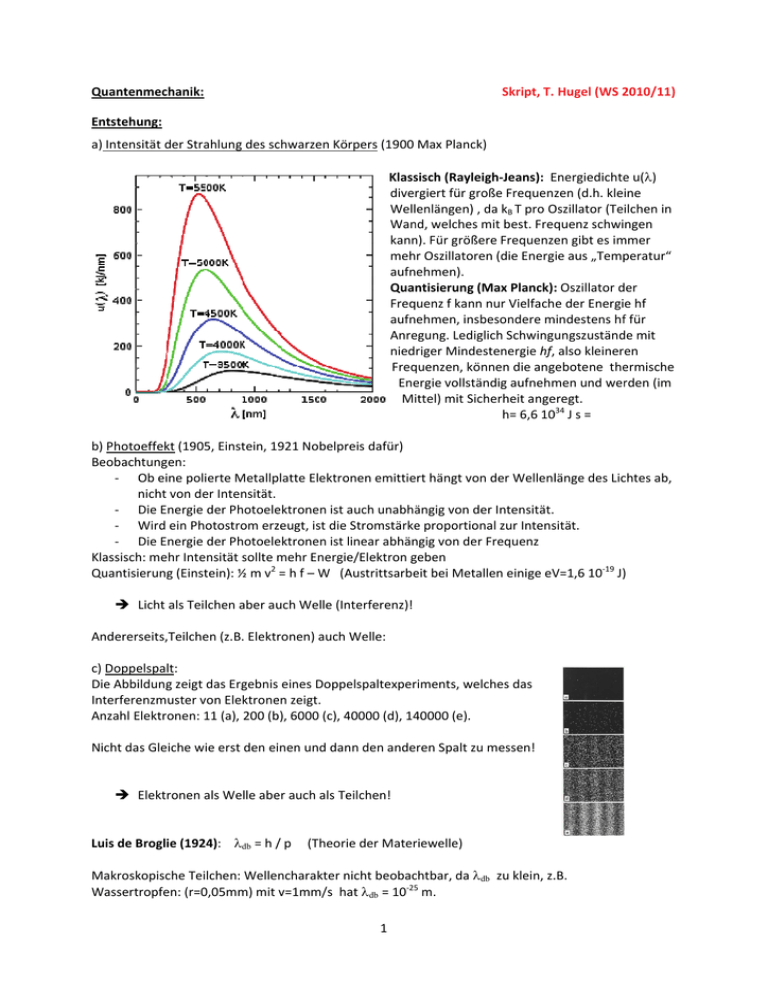
Quanten
nmechanik: Skript, T. Hugel (WS 2
2010/11) Entstehu
ung: a) Intenssität der Straahlung des scchwarzen Kö
örpers (1900 Max Planck)) e u(λ) Klasssisch (Rayleiggh‐Jeans): EEnergiedichte
diverrgiert für gro
oße Frequenzzen (d.h. kleine Wellenlängen) , d
da kB T pro O
Oszillator (Teilchen in nd, welches m
mit best. Freq
quenz schwingen Wan
kann
n). Für größere Frequenzeen gibt es im
mmer mehr Oszillatoren (die Energie aus „Temp
peratur“ aufnehmen). Quan
ntisierung (M
Max Planck):: Oszillator d
der Frequenz f kann nur Vielfache der Energie hf aufnehmen, insb
besondere m
mindestens hff für Anre
egung. Ledigllich Schwingungszuständ
de mit niedriger Mindesstenergie hf, also kleineren Freq
quenzen, kön
nnen die anggebotene the
ermische Ene
ergie vollstän
ndig aufnehm
men und werrden (im Miittel) mit Sich
herheit angeeregt. h= 6,6 10
034 J s = b) Photo
oeffekt (1905
5, Einstein, 1921 Nobelprreis dafür) Beobach
htungen: erte Metallp
‐ Ob eine poli
O
platte Elektro
onen emittiert hängt von
n der Wellenllänge des Licchtes ab, nicht von deer Intensität. ‐ Die Energie d
der Photoeleektronen ist auch unabhäängig von deer Intensität. ‐ Wird ein Pho
W
otostrom erzzeugt, ist die Stromstärke
e proportion
nal zur Intenssität. ‐ Die Energie d
der Photoeleektronen ist linear abhän
ngig von der Frequenz Klassisch
h: mehr Inten
nsität sollte mehr Energie/Elektron ggeben Quantisierung (Einsttein): ½ m v2 = h f – W (A
Austrittsarbe
eit bei Metallen einige eV
V=1,6 10‐19 J)) Î Licht als Teilchen aber au
uch Welle (In
nterferenz)!
Andererseits,Teilcheen (z.B. Elektronen) auch Welle: c) Doppeelspalt: Die Abbiildung zeigt d
das Ergebniss eines Doppelspaltexperriments, welcches das Interfereenzmuster vo
on Elektroneen zeigt. Anzahl EElektronen: 1
11 (a), 200 (b
b), 6000 (c), 4
40000 (d), 14
40000 (e). Nicht das Gleiche wie erst den eiinen und dan
nn den anderen Spalt zu messen! Î Elektronen aals Welle abeer auch als Teeilchen! Luis de B
Broglie (1924
4): λdb = h // p (Theorie der Materriewelle) nicht beobacchtbar, da λdb
Makroskkopische Teillchen: Wellencharakter n
d zu klein, z..B. Wassertropfen: (r=0,05mm) mit v=1mm/s hat λdb = 10‐255 m. 1 Heisenberg’sche Unschärferelation (1927): Δp Δx ≥ h Impuls und Ort eines Teilchens können nicht gleichzeitig beliebig genau bestimmt werden. Motivation ( für x‐Komponente): Teilchen im Mikroskop betrachtet: Δx ≈ λ / sin α Teilchen wird bei der Beobachtung mit Photonen mit Impuls p unter einem Winkel (bis zu) α getroffen: ‐> Δp ≈ p sin α = h/λ sin α ‐> Δp Δx ≈ h Konzeptionelle Probleme: Oft ist klar, wann Welle‐ oder Teilchencharakter: Sandkorn: m=10‐6 g, v=10‐3m/s ‐> λdb = 10‐21 m = 10‐11 Å. Elektron 100 eV, λdb = 10‐10 m ‐> Beugung am Kristall wie eine Welle Damit kommt man im Alltag relativ weit, aber nicht in der Chemie (z.B. Beschreibung von Atomen und Molekülen). Problem: Wer entscheidet im Zweifel ob Welle oder Teilchen? Noch problematischer: Interferenz gibt es auch für einzelne Photonen / Teilchen ‐> sie ist kein kollektiver Effekt! Trotzdem kann ein Photon nur durch Spalt 1 oder Spalt 2 ‐ Photonen können nicht in Teile zerlegt werden. Nur Spalt 1 offen: P1(r,t) Nur Spalt 2 offen: P2 (r,t) Beide Spalte offen: Pges ≠P1+P2 (jedes Photon muss mit sich selbst interferieren) Experimenteller Beweis: Neutronenexperiment bei dem nur ein Neutron im Schnitt im Experiment ist ‐> trotzdem Interferenz, es wird nie ein halbes Neutron detektiert ‐> Das Neutron müsste durch den Spalt beeinflusst sein, durch den es nicht ging. Heutige Interpretation: Ganze Messapparatur / Messung entscheidet ob Welle oder Teilchen. z.B. zerstört die Detektion des Neutrons die Phasenbeziehung zwischen den Wellen durch die Spalte Î Konzentration auf Observable (keine Rückschlüsse auf physikalische Eigenschaften / Größen, die nicht beobachtet werden können – z.B. „Schrödingers Katze“). Messung in der Quantenmechanik: Operator, dieser „zwingt“ das System (Ψ) auf eine Eigenfunktion/Eigenvektor (bei Katze z.B. tot oder lebendig). Der Eigenwert ist dann das Ergebnis der Messung. Ô ΨEigen = a ΨEigen
Beispiel: 2-Dim. Fläche
Jeder Punkt ist durch x,y Wert beschrieben.
2
Nehme z.B. Operator, der um 2 in x-Richtung verschiebt: Ô
Beispiel für Eigenvektor: (
1
0
Beispiel für kein Eigenvektor: (
Ô
1
1
1
0
Ô
3
0
1
1
3
3
1
2 1
0
-> Eigenwert: 3
1
1
Beispiel für Eigenfunktion:
Operator: wieder Verschiebung um +2 in x‐Richtung F(x)=sin (kx) ‐> ÔF(x) = sin (k[x+2]) = sin (kx + 2k) Eigenfunktion sind alle f(x) für die gilt: a) k =m π , d.h. λ = 2π/k =2/m ‐> Eigenwert a=1 b) k= (m+1/2) π ‐> Eigenwert a=‐1
Jetzt brauchen wir nur noch die Funktion (Ψ) und die Operatoren für die Messgrößen. Ψ erfüllt die Schrödinger Gleichung – dafür gibt es keinen strikten Beweis, aber mehrere plausible Herleitungen (z.B. aus der Wellengleichung), bisher noch kein Gegenbeispiel. Die Schrödinger Gleichung (1925):
Stationär in einer Dimension:
Lösung zum Beispiel:
Freies Teilchen: Eges – Epot = Ekin = p2/2m =
Beispiel: Potentialstufe
(z.B. ebene Lichtwelle fällt auf die Grenzfläche Luft-Materie (z.B. Glas))
Teilchen an Potentialstufe: Epot = E0 für x > 0
Bereich (I):
Stationäre Schrödingergleichung mit Epot=0
− h2 ∂ 2Ψ
= E ges Ψ
2m ∂x 2
E = p2/2m =
h 2k 2
2m
∂2Ψ
Î
= −k 2 Ψ
2
∂x
Lösung: ΨI(x) = A eikx + B e-ikx
Bereich (II):
∂ 2 Ψ 2m
+ 2 ( E − E0 ) Ψ = 0
∂x 2
h
Î
∂ 2Ψ
− α 2Ψ = 0
2
∂x
α ≡ 1 h 2 m( E0 − E )
Lösung: ΨII(x) = C eα x + D e-α x
3 Gesamt: Ψ(x) = ΨI für x <0 und ΨII für x >0 und stetig differenzierbar, d.h.:
a) ΨI(x=0) = ΨII (x=0) -> A+B = C+D
⎡ ∂Ψ ⎤
(1)
⎡ ∂Ψ ⎤
b) ⎢ I ⎥ = ⎢ II ⎥
⎣ ∂x ⎦ 0 ⎣ ∂x ⎦ 0
(2)
2 Fälle: E=Ekin der einfallenden Welle ist größer oder kleiner als die Potentialstufe
a) E < E0
A=reell -> C=0, sonst ΨII(x) nicht normierbar)
Aus (1): D=A+B
Aus (2): ik (A-B) = -α(A+B) -> B =
Mit D=A+B ‐> D =
ik + α
A ik − α
2ik
A ik − α
Reflektivität: R=
Be − ikx
Ae
2
ikx 2
=
B
2
A
2
=
ik + α
ik − α
2
=
(ik + α )(−ik + α )
= 1 (ik − α )(−ik − α )
Î Alle Teilchen werden reflektiert, aber Teilchen dringen ein:
Einschub: Interpretation (Kopenhagen , 1927 von Born und Heisenberg)
(bis heute überwiegende, obwohl inzwischen viele andere Interpretationen):
|
,
| ist die Wahrscheinlichkeitsdichte am Ort x zur Zeit t
-> |
, |
dV zu finden.
gibt die Wahrscheinlichkeit an, das Teilchen zur Zeit t im Volumenelement
|
,
|
1
Im Beispiel: Wahrscheinlichkeit W(x) ein Teilchen an x>0 zu finden:
2
W(x)= ΨII ( x) = De −αx
2
=
4k 2
4k 2 2 −2αx
2 − 2αx
A
e
=
A e k 02
α2 + k2
Nach x=1/2α ist die Eindringwahrscheinlichkeit auf 1/e abgesunken.
Tunneleffekt: (Barriere ist höher als die Energie der einfallenden Welle, aber nur endlich (a) breit: Skizze) Klassisch: Transmission T=0 für E<E0 QM: Analoge Rechnung mit Randbedingungen zu oben T≈
16 E
( E0 − E )e −2αa 2
E0
„Tunneleffekt“ 4 k02=2mE0/ħ2
Beispiele: 1) E = ½ E0 a = λ =
‐> α a = 1 h
2mE
T = 0,42 2) Alpha-Zerfall (Skizze)
3) Inversionsschwingung im NH3 Molekül
4) Photoeffekt ist KEIN Tunneln!
b) E>E0
Klassisch: alle Teilchen gehen weiter, aber abgebremst: Ekin=E-E0
QM:
α ≡ 1 h 2m( E0 − E ) imaginär
2 m ( E − E0 )
Reelle Größe: k‘= iα = 1
h
Damit: ΨII(x) = C e-ik‘x + D eik’x
Da für x>0 kein Fluss in negativer x-Richtung: C=0
Aus (1) und (2) folgt analog zu oben:
B=
k − k'
A k + k'
ikx
−> ΨI(x) = Ae + A
->
ΨII(x) = A
D=
2k
A
k + k'
k − k ' −ikx
e k + k'
2k ik 'x
e
k + k'
‐> Wellenlänge ändert sich (aber nicht die Energie!), manche „Teilchen“ werden reflektiert (rücklaufende Welle)
5 Postulate der Quantenmechanik
1) Für jedes dynamische System existiert eine Wellenfunktion Ψ(x,t) aus der alle möglichen
Vorhersagen der physikalischen Eigenschaften des Systems erhalten werden können.
2) Jede dynamische Variable kann durch Operator (hermitschen, reeller Eigenwert) repräsentiert
werden, dessen Eigenwert die möglichen Ergebnisse einer Messung sind. Unmittelbar nach
der Messung entspricht Ψ(x,t) der Eigenfunktion zu diesem Eigenwert.
3) Operatoren für die Position und den Impuls eines Teilchens (1-D) sind x und
.
Operatoren für andere dynamische Größen haben die gleiche funktionale Beziehungen dazu
wie in der klassischen Physik.
4) Bei einer Messung repräsentiert durch den Operator Ô an der Wellenfunktion Ψ is die
Wahrscheinlichkeit, dass das Ergebnis ein bestimmter diskreter Eigenwert am ist: | |
∑
. Nach der Messung ist das System in der Eigenfunktion zum gemessenen
Wobei
Eigenwert.
5) Die Entwicklung der Wellenfunktion mit der Zeit ist durch die zeitabhängige
Schrödingergleichung gegeben.
Zeitabhängige Schrödingergleichung in drei Dimensionen:
2
Beispiele – Motivationen:
Zu 1):
Klassischer Mittelwert:
f(v) ist die Wahrscheinlichkeit, dass ein Teilchen eine Geschwindigkeit im Interwall v bis v+dv hat.
|
|
QM:
Viele Messungen: Verteilung der Messgröße x um <x>,NICHT durch Messfehler, sondern
durch Unschärfe!
Zu 3):
Klassische Energie: Ekin = p2 / 2m
QM: p2/2m =
-> Schrödingergleichung: Ekin + Epot = Eges
Zu 4): Beispiel: Ψ(x) = [2 sin (πx) + 3 sin (3/2 π x)] 1
√13
‐> q1 = 2
Einschub: Weitere Beispiele: Teilchen im Potentialkasten: Î Energieniveaus mit Eigenfunkionen: Ψn(x)= C sin
(n π x/a)
Î
(E2=4E1, E3=9E1)
Ψ2 = Aufenthaltswahrscheinlichkeit
Bei harmonischem Potential:
Äquidistante Energien:
6 √13
q2= 3
√13