Theoretischer Teil - antriebstechnik.fh

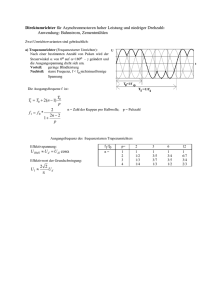
Leistungselektronik
Versuch 4, Selbstgeführte Stromrichter
4.1 DC/DC-Wandler im Einquadrantenbetrieb
4.1.1 Allgemeines
Die einfachsten Topologien eines DC/DC-Wandlers führen Ströme und Spannungen
jeweils nur mit einem vorgegebenen Vorzeichen, d.h. im Einquadrantenbetrieb. Zu
nennen sind in diesem Zusammenhang speziell der Hochsetzsteller und der
Tiefsetzsteller. Sie können als Prototypen selbstgeführter Stromrichter angesehen
werden. Schaltnetzteile - also sämtliche Spannungsversorgungen von
Elektronikkomponenten - funktionieren zum Teil nach den im Folgenden diskutierten
Funktionsprinzipien des Hoch- bzw. Tiefsetzstellers. Im Bereich höherer Leistungen
werden diese DC/DC-Wandler dann für einen 4-Quadarntenbetrieb ergänzt für
drehzahlgeregelte Antriebe mit Gleichstrommaschinen angewandt. In der Form bzw.
mit der Topologie eines 4-Quadrantenstellers ist der DC/DC-Wandler auch nicht
mehr von einem einphasigen Wechselrichter zu unterscheiden. Es handelt sich hier
nur noch um eine Frage der Definition: Was ist noch eine variable Gleichspannung
und was ist bereits eine Wechselspannung variabler Frequenz?
Der Tiefsetzsteller bietet die einfachste Möglichkeit möglichst effizient eine
Gleichspannung auf einen geringeren Wert zu reduzieren. Der Hochsetzsteller stellt
das duale Pendant zum TSS dar: Er bietet die einfachste Möglichkeit einen
Gleichstrom möglichst effizient im Wert zu reduzieren. Da elektrische Energiequellen
meist durch Spannungsquellen repräsentiert werden, spricht man nicht von einem
Strom-Tiefsetzsteller sondern von einem Spannungs-Hochsetzsteller (aufgrund der
Leistungsinvarianz (Verluste vernachlässigt) der Stromrichter kann man bei einer
Anpassung von Spannung oder Strom immer von einem reziproken Verhalten des
jeweils zugehörigen Stroms bzw. der zugehörigen Spannung ausgehen).
Abb. 1: Tief- und Hochsetzsteller als Schaltzellen mit Umschalter und mit
Leistungshalbleitern realisiert (mit Ld -> ∞)
Leistungselektronik
In Abbildung 1 sind die Grundlegenden Schaltungen mit idealen Umschaltern
gezeigt. Sie speisen jeweils eine ohmsch-induktive bzw. ohmsch-kapazitive Last. Da
die Schalter dieser Stromrichter sehr schnell im Vergleich zu den jeweiligen
Zeitkonstanten (τL = L/RL bzw. τL = RLC) hin- und herschalten, können die eigentlich
passiven Lasten während der Schalthandlungen als konstante Strom- bzw.
Spannungsquellen angesehen werden. Der TSS schaltet als eine konstante
Spannung „portionsweise“ auf eine ohmsch-ind. Last bzw. eine – für den jeweiligen
Zeitbereich – konstante Stromquelle. Der HSS wiederum einen konstanten Strom
„portionsweise“ auf eine ohmsch-kap. Last bzw. auf eine – für den jeweiligen
Zeitbereich – konstante Spannungsquelle. Es ist hier schon zu erahnen, dass für
einen rückspeisefähigen DC/DC-Wandler nun jeweils einer dieser beiden
Stromrichter benötigt wird
Einen TSS für den Leistungstransfer von
Spannungsquelle (bzw. hohem Spannungsniveau) zu Stromquelle (bzw. niedrigem
Spannungsniveau) und einen HSS für die Gegenrichtung. Die Schalter sind als
Umschalter realisiert, da sich immer auf der einen oder anderen Seite der Schaltung
eine ohmsch-induktive Last und/oder eine Stromquelle befindet die stets einen
Strompfad erfordert. Wird dieser nicht gewährleistet, hat dies eine Bauteilzerstörung
aufgrund von Überspannungen und schließlich Durchschlag zur Folge.
Die Zeitverläufe von Strom und Spannung am Ausgang uL, iL der jeweiligen
Schaltung sind im Falle einer resistiven Last proportional zueinander und können für
beide Schaltungen gemäß Gleichung (1) und (2) jeweils abschnittsweise für den
Tiefsetzsteller bzw. Hochsetzsteller bestimmt werden. Mit der Normierung der
Lastströme und –spannungen (3) kann unter der Annahme von gleichen
Zeitkonstanten (4) ein normierter Zeitverlauf für die Ausgangsgrößen gemäß Abb. 2
gefunden werden.
Tiefsetzsteller:
L
L
 
−t
−t

RL 
RL

U 0 1 − e
+ u (nT )e
für nT < t < (nT + TE )
 L
 
u L (t ) =  

L

−t
u L (nT + TE )e RL
für (nT + TE ) < t < ((n + 1)T )
(1)
Hochsetzsteller:
t
t

−
−


CRL 
CRL

 RL I 0 1 − e
+ u (nT )e
für nT < t < (nT + TE )

 L



u L (t ) = 
t

−
u L (nT + TE )e CRL
für (nT + TE ) < t < ((n + 1)T )
(2)
Normierung und Annahme gleicher Zeitkonstanten (Beispiel!):
x L (t ) =
u L iL
=
U0 I0
τ L = CRL =
L
⇒ RL =
RL
(3)
L
C
(4)
Leistungselektronik
Abb. 2: Normierter Zeitverlauf der Ausgangsspannungen und –ströme für Hoch- und
Tiefsetzsteller bei gleicher Lastzeitkonstante
Für einen periodischen Schaltzyklus mit der Periodendauer T meint TE die
Schaltphase, in der der Umschalter den oberen Schaltzustand einnimmt und
TA = T - TE die Phase, in der er die untere Stellung einnimmt. Für den TSS entspricht
TE der Ansteuerungsphase für den korrespondierenden Leistungshalbleiter, bei dem
HSS ist es TA.
In dem hier gezeigten Fall sind Strom und Spannung nach dem Einschalten stets
größer null. Die jeweilige elektrische Ausgangsgröße „lückt“ also nicht. Unter einem
lückenden Zeitverlauf versteht man den Fall, dass die jeweilige elektrische Größe
periodisch null wird. Der Maximalwert der jeweiligen elektrischen Ausgangsgröße
kann mit (5) berechnet werden, der Mittelwert wird mit (6) abgeschätzt, wobei die
Randbedingung (7) für die meisten selbstgeführten Stromrichter zutrifft, womit (6) zu
hinreichend genauen Ergebnisse führt. Es können für diesen Fall auch die
vereinfachten Ersatzschaltbilder aus Abbildung 3 gefunden werden. Dies bedeutet,
dass mit (7) für den zumeist betrachteten stationären Zustand der Schaltung ein
jeweiliger Gradenverlauf angenommen werden kann. Diese Näherung erleichtert die
analytische Behandlung dieser Stromrichterschaltungen enorm, wie noch zu sehen
sein wird.
Maximaler normierter Ausgangswert (im stat. Zustand):
xL max =
1− e
1− e
−
−
TE
τL
T
(5)
τL
Mittlerer normierter Ausgangswert (im stat. Zustand):
TE
T
für den Fall, dass:
τ L >> T
xL =
(6)
(7)
Leistungselektronik
Abb. 3: Vereinfachung der Schaltungen aus Abb. 1 mit der Bedingung τL >> T
Tiefsetzsteller
Hochsetzsteller
U L = xU 0
U L = x RL I 0
4.1.2 Steuerung Tiefsetzsteller
Für die folgenden Betrachtungen wird die Lastspannung UL ebenso wie die
Eingangspannung Ue = U0 als konstant angenommen. Für nicht lückenden Betrieb
des Laststroms iL kann dann für den stationären Betrieb (Mittelwert des Laststroms
ändert sich nicht) ein fester Bezug zwischen Ein- und Ausgangsspannung sowie der
Einschaltzeit des Halbleiterschalters V1 in Bezug auf die Schaltperiode T gefunden
werden (8). Dabei ist a der Aussteuerungsgrad (englisch duty cycle, D).
Aussteuerungsgrad für nicht lückenden Betrieb
TE
U
=a= L
T
Ue
(8)
Weicht der Aussteuerungsgrad a von diesem Wert ab (bei konstanten
Spannungsquellen Ue und Ua), so wird für sinkende Werte von a immer noch ein
stationärer Zustand erreicht, allerdings bei lückendem Strom. Für steigende Werte
von a ist ein stetig steigender Laststrom die Folge (woraus sich allerdings bei einem
realen Aufbau wiederum eine Anpassungen der Lastspannung UL ergibt). In
Abbildung 4 sind die Laststromverläufe des TSS für a < UL/Ue, a = UL/Ue sowie
a > UL/Ue angegeben. Für den Fall lückenden Laststroms kann der Mittelwert (10)
sowie der Effektivwert (11) des Laststroms als Funktion der hier angegeben
Parameter mit ermittelt werden. Bei nicht lückendem Strom kann lediglich eine
Aussage über den Wechselanteil des Laststroms (12) gemacht werden.
Leistungselektronik
Abb. 4: Laststromverläufe bei konstantem Verhältnis UL/Ue und variablem
Aussteuerungsgrad a
Stromschwankungsbreite des Laststroms:
∆i L = (U e − U L )
aT
L
(9)
Mittelwert des Laststroms, lückend:
i L ,lück
 Ue
 a 2T

= Ue
− 1
U
 L
 2L
(10)
Effektivwert des Laststroms, lückend:
aT U e
~
I L ,lück = (U e − U L )
L UL
(11)
Effektivwert des Wechselanteils im Laststrom, nicht lückend:
aT
~
I L ~ = (U e − U L )
3L
(12)
4.1.3 Steuerung Hochsetzsteller
Für die folgenden Ausführungen zum HSS wird wiederum die Lastspannung UL
ebenso wie die Eingangspannung Ue jeweils als konstant angenommen. Außerdem
habe nun die Induktivität Ld entgegen der Annahmen aus 4.1.1 einen endlichen Wert.
Für nicht lückenden Betrieb des Eingangsstroms ie kann im Fall eines stationären
Betriebs (Mittelwert des Eingangsstroms ändert sich nicht) ein fester Bezug zwischen
Ein- und Ausgangsspannung sowie des Aussteuerungsgrades des
Halbleiterschalters V1 gefunden werden (13).
Leistungselektronik
Aussteuerungsgrad für nicht lückenden Betrieb
TE
U
= a =1− e
T
UL
(13)
Auch beim HSS resultiert wie zuvor beim TSS für sinkende Werte von a ein
stationärer Zustand bei lückendem Drosselstrom (hier allerdings lückender
Eingangsstrom ie). Für steigende Werte des Aussteuerungsgrades folgt auch hier ein
stetig steigender Drosselstrom ie, siehe auch Abb. 5. Die korrespondierenden
Kenngrößen sind mit (14) – (17) angegeben.
Stromschwankungsbreite des Eingangsstroms:
∆i e = U e
aT
L
(14)
Mittelwert des Eingangsstroms, lückend:
ie ,lück =
U eU L a 2T
U e − U L 2L
(15)
Effektivwert des Eingangsstroms, lückend:
aT
~
I e ,lück = U e
L
aU L
3 (U L − U e )
(16)
Effektivwert des Wechselanteils im Eingangsstrom, nicht lückend:
aT
~
I e ~= U e
3L
(17)
Abb. 4: Eingangsstromverläufe bei konstantem Verhältnis Ue/UL und variablem
Aussteuerungsgrad a
Leistungselektronik
4.1.4 Zusätzliche Berechnungsvorschriften
Bisher wurden lediglich der Laststrom für den TSS sowie der Eingangsstrom für den
Hochsetzsteller angesprochen. Mittel- und Effektivwerte der jeweils noch fehlenden
Eingangs- bzw. Ausgangsströme stellen ebenso wesentliche Kenngröße dar. Sie
können allerdings aus den bereits bestimmten Größen konstruiert werden, da sie
entweder zeitweise mit den bereits bestimmten Stromverläufen identisch oder null
sind. Dies ist in Abb. 5 exemplarisch für TSS wie HSS im Fall von stationär nicht
lückenden Drosselströmen zu sehen. D.h. die Berechnung der jeweiligen Mittel- und
Effektivwerte beschränkt sich auf die Bestimmung dieser Kennwerte für
trapezförmige Zeitverläufe (18) - (21), wobei die Parameter i1 und i2 mit den oben
angeführten Ausdrücken bereits bestimmt werden können (mit i1,2 = ī ± ∆i/2).
Mittelwert des Eingangsstroms beim TSS
ie = a
i1 + i2
2
(18)
Mittelwert des Ausgangsstroms beim HSS
ie = (1 − a )
i1 + i2
2
(19)
Effektivwert des Eingangsstroms beim TSS
(
a 2
~
2
Ie =
i1 + i1i2 + i2
3
)
(20)
Effektivwert des Ausgangsstroms beim HSS
(
1− a 2
~
2
Ie =
i1 + i1i2 + i2
3
)
(21)
Abb. 5: Links: Eingangsstromverlauf beim TSS, rechts: Ausgangsstromverlauf beim
HSS jeweils bei nicht lückendem Drosselstrom
Leistungselektronik
4.2 Ergänzung der Schaltungen für 2Q- bzw. 4Q-Betrieb
4.2.1 Konstruktion von 2Q-DC/DC-Wandlern und deren Ansteuerung
Durch geschickte Ergänzung der bisher gezeigten grundlegenden Schaltungen mit
nur zwei weiteren Leistungshalbleitern ist nun jeweils für die resultierenden
Stromrichter ein Betrieb in zwei Quadranten der Ausgangsgrößen-Kennlinienebene
(ua(ia)) möglich. Die Ansteuerung der Leistungshalbleiter und die Definition des
Aussteuerungsgrades muss hierbei mitunter angepasst werden. Es wird im
Folgenden immer davon ausgegangen, dass der Betrag der Eingangsspannung
größer sei als jener der Last- bzw. Ausgangsspannung |Ue| > |ûa|, damit eine
Steuerbarkeit der Schaltung erhalten bleibt. In Tabelle 1 sind die jeweiligen
Schaltungen zusammen mit den ihnen zugänglichen Quadranten der
Ausgangskennlinienebene gezeigt. Es sind für die Einzelnen Schaltungen zudem die
angesteuerten Leistungshalbleiter für den jeweiligen Leistungsfluss kenntlich
gemacht. In den Fällen, bei denen jeweils zwei Halbleiterschalter als anzusteuernde
Bauteile gekennzeichnet sind, wird von einer synchronen Ansteuerung der Bauteile
ausgegangen, d.h. die korrespondierende Einschaltphase TE sowie der
Aussteuerungsgrad a bezieht sich auf beide Bauteile gleichzeitig. In den Fällen, für
die zwei Schaltungen in einer Zeile angegeben sind, heißt dies, dass entweder die
eine oder die andere Möglichkeit der Ventilansteuerung gleichberechtigt zum
gewünschten Leistungsfluss führt.
Mögliche
Quadranten
a
b
Angesteuerte LHL-Schalter für jeweiligen Leistungsfluss
P von Ue -> Ua (TSS-Betrieb)
P von Ua -> Ue (HSS-Betrieb)
Leistungselektronik
c
d
Tab. 1: Mögliche Schaltungskombinationen für 2Q-DC/DC-Wandler
4.2.2 Konstruktion eines 4Q-DC/DC-Wandlers sowie dessen Ansteuerung
Es ist nun auch möglich einen Stromrichter für alle vier Quadranten der
Ausgangskennlinienebene zu konstruieren, siehe Abb. 6. Es ist allerdings bei einem
solchen Stromrichter nicht mehr sinnvoll die Ansteuerung der Ventile mit einem
Aussteuerungsgrad a zu beschreiben. In Tabelle 2 sind sämtliche mögliche
Kombinationen von geschlossenen Ventilen und die dazu gehörigen Werte für die
Ausgangsspannung ua gezeigt. Es ist sofort klar, dass die Schaltkombinationen, bei
denen beide Leistungshalbleiter einer Halbbrücke geschaltet werden, verboten sind,
da sie zu einem Kurzschluss der Eingangsspannung führen würden. Nach welchem
Prinzip und in welcher Abfolge die hier gezeigten Schaltkombinationen angewandt
werden, wird im nächsten Abschnitt geklärt.
Abb. 6: Selbstgeführter 4-Qudaranten-Stromrichter
Leistungselektronik
Eingeschaltete
Halbleiterschalter
Schaltzustand in vereinfachter Schaltung
mit Umschaltern
Resultierender
Momentanwert der
Ausgangsspannung ua
V1, V4
Ue
V1, V3
0
V2, V4
0
V2, V3
-Ue
Tab. 2: Mögliche Schaltungskombinationen (eingeschaltete Halbleiterschalter) des 4Q-Stellers
Leistungselektronik
4.3 Pulsweitenmodulation eines 4Q-DC/DC-Wandlers bzw. einphasigen
Wechselrichters
Aus Tabelle 2 wird ersichtlich, dass die Ausgangsspannung ua insgesamt lediglich
drei verschiedene Momentanwerte abhängig von den Schalterzuständen S1 sowie
S2 annehmen kann. Sieht man den zeitabhängigen Schaltzustand der beiden
Umschalter S1 und S1 als Funktion mit der Zeit s1(t) und s2(t), die lediglich die
diskreten Werte 1 und -1 annehmen können, so kann der Mittelwert der
Ausgangsspannung ua über eine Schalt- oder auch Trägerperiodendauer TC (Index C
für Carrier = Träger) wie folgt geschrieben werden (22).
ua = Ua =
Ue
2TC
∫ (s (t ) − s
TC
1
2
(t ) )dt
(22)
Anhand von Gleichung (22) wird ersichtlich, dass man mit dieser
Stromrichterschaltung nun nicht mehr nur reine Gleichspannungen sondern auch
Spannungsverläufe mit einem Wechselspannungsanteil darstellen kann.
Die Ermittlung der entsprechenden Schaltpulse für einen gewünschten
Gleichspannungs- oder auch Wechselspannungsverlauf erfolgt mittels einer so
genannten Pulsweitenmodulation, PWM. Bei der Pulsweitenmodulation wird eine
Modulationsfunktion m(t) (Wertebereich: m(t) = -1..1) mit einer Trägerfunktionen
cn(t) = -1..1 verglichen. Die Modulationsfunktion m(t) ist für den Fall, dass der
Stromrichter als 4Q-DC/DC-Wandler genutzt wird, ein konstanter Parameter, solange
der Betriebspunkt nicht geändert wird. Für Wechselrichterbetrieb ist m(t) meist eine
Sinusfunktion - gelegentlich auch eine Rechteckfunktion - variabler Frequenz f g. Die
Trägerfunktion ist allgemein eine Dreieckfunktion mit beliebiger Flankensteilheit. Sie
kommt normalerweise entweder als reiner Sägezahn fallender oder steigender
Flanke oder als symmetrisches Dreieck vor. Gleichungen (23) – (25) zeigen drei
verschiedene Modulationsfunktionen. Hier ist der Parameter M der Modulationsgrad,
der zunächst auf den Wertebereich M = 0..1 begrenzt bleiben soll. Es stellt sich
heraus, dass für den Grenzwert fC = 1/TC → ∞ der Ausdruck (26) gefunden werden
kann. Meist reicht für diese Annahme bereits die Bedingung, dass die
Trägerfrequenz sehr viel höher als die zu stellende Grundschwingungsfrequenz
fg = 1/Tg am Ausgang sein soll fC >> fg für ausreichend genaue Ergebnisse aus.
Modulationsfunktion für DC/DC-Wandler-Betrieb
m(t ) = M
(23)
Rechteck-Modulationsfunktion
Tg

M für 0 ≤ t <
2
m(t ) = 
− M für TC ≤ t < T
g

2
(24)
Leistungselektronik
Sinus-Modulationsfunktion
m(t ) = M sin(ω g t )
(25)
Zusammenhang Modulationsfunktion und Schaltfunktionen
m(t ) =
1
2TT
∫ (s (t ) − s
TC
1
2
(t ) )dt
(26)
Bei der einfachen PWM wird die Modulationsfunktion m(t) mit nur einem Träger c(t)
verglichen. Sollte der Momentanwert der Modulationsfunktion m(t) größer sein als der
der Trägerfunktion c(t) so gilt s1(t) = 1 und s2(t) = -1 sowie umgekehrt (27). Bei der
einfachen PWM nimmt die Ausgangsspannung ua nur zwei mögliche Momentanwerte
an, wie in Abb. 7 gut zu sehen ist.
Hinsichtlich des resultierenden Oberschwingungsgehaltes im Ausgangsstrom wäre
es allerdings wünschenswert auch den dritten Momentanwert 0 für die
Ausgangsspannung zu nutzen. Dies ist möglich mit der Einführung eines zweiten
Trägers, der die gleiche Form, wie der erste besitzt, allerdings in seiner
Grundschwingungsperiode um den Winkel γ = π zur ersten Trägerfunktion
verschoben ist. Nun hat jede Halbbrücke des Stromrichters quasi eine Trägerfunktion
bekommen und sie werden nun unabhängig voneinander und nicht mehr
komplementär geschaltet. Wenn nun nämlich die Modulationsfunktion m(t) größer ist
als c1(t), so wird s1(t) = 1 und im umgekehrten Fall s1(t) = -1. Das invertierte Prinzip
wird mit dem Vergleich von m(t) zu c2(t) und s2(t) angewandt, (28). Die genaue
Phasenverschiebung von γ = π zwischen den beiden Trägerfunktionen sorgt dabei
dafür, dass die Ausgangsspannung ua abhängig vom Vorzeichen des
Momentanwertes der Modulationsfunktion m(t) einen nur noch unipolaren Verlauf
hat, wie in Abb. 8 zu sehen ist.
Werte der Schaltfunktionen für einfache PWM (mit einem Träger)
1
s1 (t ) = 
− 1
− 1
s 2 (t ) = 
1
für m (t ) > c (t )
für 1 für m (t ) < c (t )
für m (t ) > c (t )
(27)
für 1 für m (t ) < c (t )
Werte der Schaltfunktionen für PWM mit zwei Trägern
1
s1 (t ) = 
− 1
− 1
s 2 (t ) = 
1
für m (t ) > c1 (t )
für 1 für m (t ) < c1 (t )
für m (t ) > c2 (t )
für 1 für m (t ) < c2 (t )
(28)
Leistungselektronik
M(t)
c(t)
s1(t)
s2(t)
ua(t)/Ue
ia(t)
ie(t)
Abb 7: „Einfache“ Pulsweitenmodulation mit einem Träger
M(t)
c(t)
s1(t)
s2(t)
ua(t)/Ue
ia(t)
ie(t)
Abb 8: Pulsweitenmodulation mit zwei Trägern
Leistungselektronik
4.4 Berechnung von Kenngrößen eines 4Q-DC/DC-Wandlers bzw. einphasigen
Wechselrichters
Anhand der Abbildungen 7 und 8 kann man unschwer erkennen, dass die
Ausgangsspannung – wenngleich im Verlauf des gleitenden Mittelwertes der
Modulationsfunktion vergleichbar – einen sehr starken hochfrequenten Wechselanteil
besitzt. Dies macht sich auch in einem vom Grundschwingungseffektivwert stark
abweichenden Gesamteffektivwert bemerkbar. Darüber hinaus sorgt das periodische
Umschalten der Schalter S1 und S2 (eigentlich sind es die Ventile V1 – V4, die
geschaltet werden) dafür, dass der Eingangsstrom ständig zwischen den Werten +ia,
0 und -ia umgeschaltet wird. Er nimmt also - abhängig vom Modulationsverfahren abschnittsweise den Momentanwert des Ausgangsstroms mit pos. bzw. neg.
Vorzeichen oder aber den Wert 0 an. Der Gleichanteil des Eingangsstroms lässt sich
relativ einfach über die Leistungsbilanz ermitteln, aber auch der Effektivwert des
Eingangsstroms soll hier noch ermittelt werden, da er ein Maß für die Verluste im
Zwischenkreis darstellt.
PWM-Verfahren
Ein Träger
Zwei Träger mit γ = π
Kenngröße
(Modulationsfunktion)
Mittelwert,
(Gleichspannungswandlung)
Grundschwingungseffektivwert (Rechteck)
Grundschwingungseffektivwert (Sinus)
u a = MU e
2 2
~
Ua =
MU e
1
π
M
~
Ua =
Ue
2
1
u a = MU e
2 2
~
Ua =
MU e
1
π
M
~
Ua =
Ue
2
1
Gesamteffektivwert
(Gleichspannungswandlung)
Gesamteffektivwert
(Rechteck)
~
U a = Ue
~
Ua = Ue M
~
U a = Ue
~
Ua = Ue M
Gesamteffektivwert (Sinus)
~
U a = Ue
2
~
U a = Ue
M
Tab 3: Kennwerte der Ausgangsspannung
π
Leistungselektronik
Kenngröße
(Modulationsfunktion)
Gleichanteil
(Gleichspannungswandlung)
Gleichanteil (Sinus)
Ein Träger
PWM-Verfahren
Zwei Träger mit γ = π
i e = iˆa M = i a M
ie = iˆa
M
cos ϕ a
2
i e = iˆa M = i a M
ie = iˆa
M
cos ϕ a
2
Effektivwert
(Gleichspannungswandlung)
~
I e = iˆa = ia
~
I e = M iˆa = M ia
Effektivwert (Sinus)
iˆ
~
Ie = a
2
M  cos(2ϕ a ) 
~
I e = iˆa
1 +

3
π 

Tab 4: Kennwerte des Eingangs- bzw. Zwischenkreisstroms (Rechteckmodulation
ausgeschlossen, da der entsprechende Ausgangsstromverlauf nicht ohne weiteres
anzugeben ist)