5.1.7 Energie des harmonischen Oszillators

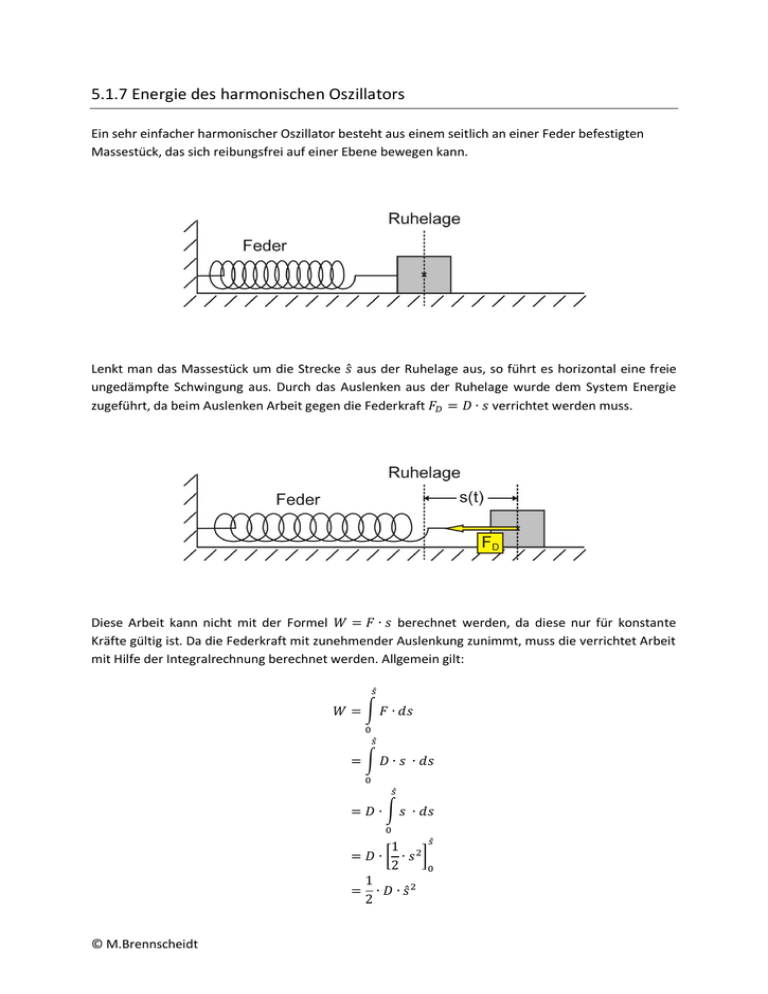
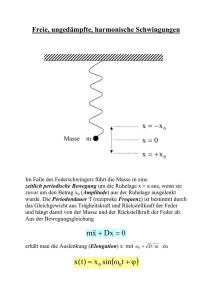
5.1.7 Energie des harmonischen Oszillators
Ein sehr einfacher harmonischer Oszillator besteht aus einem seitlich an einer Feder befestigten
Massestück, das sich reibungsfrei auf einer Ebene bewegen kann.
Lenkt man das Massestück um die Strecke aus der Ruhelage aus, so führt es horizontal eine freie
ungedämpfte Schwingung aus. Durch das Auslenken aus der Ruhelage wurde dem System Energie
zugeführt, da beim Auslenken Arbeit gegen die Federkraft
verrichtet werden muss.
Diese Arbeit kann nicht mit der Formel
berechnet werden, da diese nur für konstante
Kräfte gültig ist. Da die Federkraft mit zunehmender Auslenkung zunimmt, muss die verrichtet Arbeit
mit Hilfe der Integralrechnung berechnet werden. Allgemein gilt:
© M.Brennscheidt
Durch das Auslenken wurde dem Federpendel also die Energie
zugeführt. Diese potentielle Energie ist nicht zu verwechseln mit der aus der Mechanik bekannten
Lageenergie. Stattdessen versteht man hier unter potentieller Energie die Spannenergie des Pendels.
Da bei der Schwingung des Massestücks der Energieerhaltungssatz gilt, bleibt diese Energie während
der gesamten Schwingung erhalten und wird lediglich in andere Energieformen umgewandelt. So
wird zum Beispiel die potentielle Energie beim Durchgang durch die Ruhelage vollständig in
kinetische Energie des Massestücks umgewandelt.
Für eine beliebige Auslenkung ist somit die Summe aus potentieller Energie und kinetischer Energie
immer konstant:
Durch Einsetzen der Formeln für
und
ergibt sich dann für die Gesamtenergie:
Die Gesamtenergie kann nun auf zwei verschiedene Arten weiter umgeformt werden.
1. Energie der Oszillators bei maximaler Auslenkung:
Mit
(siehe Kapitel 4) ergibt sich:
(mit dem trigonometrischen Pythagoras
© M.Brennscheidt
Die Gesamtenergie beträgt also bei maximaler Auslenkung:
Da die Geschwindigkeit des Oszillators bei maximaler Auslenkung gleich Null ist besitzt der Oszillator
dort keine kinetische Energie, sondern lediglich potentielle Energie.
2. Energie des Oszillators beim Durchgang durch die Ruhelage:
Mit
ergibt sich:
Die Gesamtenergie beträgt also beim Durchgang durch die Ruhelage:
Beim Durchgang durch die Ruhelage ist die Geschwindigkeit des Massestücks maximal. Der Oszillator
besitzt dort keine potentielle Energie, sondern lediglich kinetische Energie.
Merksatz: Die potentielle und die kinetische Energie eines harmonischen Oszillators wandeln sich
periodisch ineinander um. Die Gesamtenergie ist konstant. Sie kann als maximale potentielle oder als
maximale kinetische Energie angegeben werden.
Die Umwandlung von potentieller in kinetische Energie und umgekehrt soll nun abschließend anhand
zweier Diagramme veranschaulicht werden:
© M.Brennscheidt
Im ersten Diagramm sind die beim harmonischen Oszillator auftretenden Energieformen in
Abhängigkeit von der Zeit aufgetragen. Es ist zu erkennen, dass die kinetische Energie (rot) immer
dann ein Maximum annimmt, wenn die potentielle Energie (blau) gleich Null ist. Umgekehrt ist die
potentielle Energie maximal, wenn die kinetische Energie Null wird. Summiert man beide
Energieformen auf, so ergibt sich zu jedem beliebigen Zeitpunkt
ein konstanter Wert, die
Gesamtenergie (grün).
In einem zweiten Diagramm ist die Energie in Abhängigkeit von der Auslenkung des Oszillators
aufgetragen.
Es ist zu erkennen, dass die potentielle Energie bei maximaler Auslenkung am größten ist und beim
Durchgang durch die Ruhelage gleich Null ist. Umgekehrt ist die kinetische Energie bei maximaler
Auslenkung gleich Null und beim Durchgang durch die Ruhelage maximal. Bei jeder beliebigen
Auslenkung ergibt erneut die Summe aus potentieller und kinetischer Energie einen konstanten
Wert. Es gilt der Energieerhaltungssatz.
© M.Brennscheidt