Vorgerechnete Aufgaben PC0 Kapitel 4

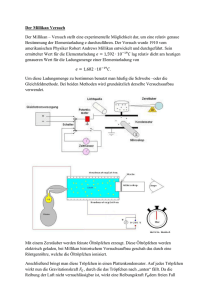
Vorgerechnete Aufgaben PC0 Kapitel 4
Aufgabe 1 (zu Elektronenbeugung an Graphit):
a) Berechne die Netzebenenabstände d1 und d2 für a = 142 pm (Abb.1).
b) Beschreibe die Gitterstruktur von Graphit. Berechne den Abstand a für MC
= 12 g/mol und ρG = 2,25 g/cm3.
Lösung:
1
Aufgabe 2 (zu Spezifische Ladung des Elektrons):
Elektronen, die durch 150 V beschleunigt worden sind, fliegen senkrecht zu
den Feldlinien in ein magnetisches Feld mit B = 0,85 mT ein und beschreiben
dort einen Kreis von 48 mm Radius.
a) Berechnen Sie e/m.
b) Mit welcher Geschwindigkeit verlassen die Elektronen die Anodenöffnung.
Wie lange brauchen Sie für einen Umlauf?
Lösung:
a)
b)
2
Aufgabe 3 (zu Elektronenbeugung an Graphit):
In einer Elektronenstrahlröhre wird eine Probe mit Elektronen durchstrahlt
und die Interferenzringe auf einem Schirm beobachtet. Bei Vergrößerung der
Beschleunigungsspannung verkleinert sich der Radius des Ringsystems.
Erklären Sie den Befund.
Lösung:
Größere Beschleunigungsspannung heißt größere Geschwindigkeit und
somit kleinere Wellenlänge. Bei kleinerem λ wird aber nach der
Braggbeziehung auch der Streuwinkel Θ kleiner. 2g sinΘ=nλ
Aufgabe 4 (zu Elektronenbeugung an Graphit):
Ein Protonenstrahl wird in einem elektrischen Feld mit einer Potentialdifferenz
von 50 V beschleunigt. Berechne für ein Proton
a) die kinetische Energie in Joule.
b) die Geschwindigkeit.
c) den Impuls.
d) die Wellenlänge.
Lösung:
Für die kinetische Energie ergibt sich mit der Ladung des Protons (q = 1,602 ·
10−19 C):
Ekin = q · ΔU = 1,602 · 10−19 C · 50 V = 8,01 · 10−18 J
Somit folgt mit Ekin = 1/2mv2 für die Geschwindigkeit des Protons:
Der zugehörige Impuls beträgt:
(4)
Die Wellenlänge ergibt sich aus der Beziehung
3
Aufgabe 5 (zu Elektronenbeugung an Graphit):
Elektronen werden durch eine Spannung von 2 kV beschleunigt. Wie groß ist
ihre de Boglie Wellenlänge?
Lösung:
v=
2 ⋅ e ⋅U
2 ⋅1.602 ⋅10 −19 ⋅ 2000V
7 m
=
=
2.65
⋅10
m
9.109 ⋅10 −31 kg
s
h
6.626 ⋅10 −34 J ⋅ s
λ=
=
= 2.7 ⋅10 −7 m
−31
7
−1
m ⋅ v 9.109 ⋅10 kg ⋅ 2.65 ⋅10 m ⋅ s
€
Aufgabe 6:
Wie groß muss die an einen Plattenkondensator angelegte Spannung U sein,
um ein negativ geladenes Öltröpfchen zwischen den waagerecht angeordneten Platten schweben zu lassen? Der Plattenabstand d beträgt 2mm. Das Öltröpfchen hat einen Radius r von 1µm und trägt eine Ladung, die dem -10 fachen der Elementarladung e entspricht. Das Öl hat eine Dichte ρOel von
875,3kg/m3.
Lösung: Damit das Öltröpfchen schwebt, muss die Summe aus der Gewichtskraft und der aus dem elektrischen Feld resultierenden Kraft auf das
Öltröpfchen gleich Null sein. Die Vektoren beider Kräfte sind entgegen gerichtet:
FGewicht + FE−Feld = 0
(8)
m·g+q·E=0
(9)
Aus der Dichte und dem Volumen des Öltröpfchens kann dessen Masse bestimmt werden. Die elektrische Feldstärke E eines idealen Plattenkondensators ergibt sich aus E = U/d und somit folgt:
Umstellen der Gleichung und Einsetzen der Werte ergibt:
4
Bei einem 10fach negativ geladenen Öltröpfchen muss die obere Platte des
Kondensators positiv gegenüber der unteren Platte geladen sein, um zwar
mit 44,9V, damit das Öltröpfchen schwebt.
Aufgabe 7:
Ein grüner Laserstrahl mit einer Wellenlänge von 532nm trifft auf eine
schwarze Oberfläche. Wie groß ist die Kraft auf die Oberfläche, wenn
7 · 1015 Photonen pro Sekunde eintreffen?
Lösung:
Der Impuls eines Photons mit der Wellenlänge 532nm beträgt:
Unter der Annahme, dass die Photonen vollständig von der schwarzen
Oberfläche absorbiert werden, wird der gesamte Impuls übertragen. Die resultierende Kraft ist die Änderung des Impulses pro Zeiteinheit, also
5