E=m c²
Werbung
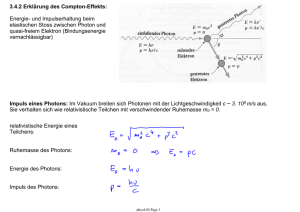
1.1.5 Masse und Impuls des Photons E=m c² Für die Photonenenergie πΈπβ = βπ lässt sich dann mit der Einsteingleichung πΈ βπ πΈ = ππ² die „Photonenmasse“ ππβ = π² = π² zuordnen. Vorsicht! Nach Einsteins Relativitätstheorie gilt auch π = π0 1− π£ π → ∞ für v → π ² d.h. die Ruhemasse des Photons muss Null sein : es gibt keine ruhenden Photonen! Der Impuls ππβ des Photons ergibt sich aus der Definition π = ππ£ zu βπ βπ β ππβ = ππβ β π = π 2 β π = π bzw. mit π = π π folgt auch ππβ = π 1.1.5 Masse und Impuls des Photons Photonen haben die Energie E, den Impuls ππ·π und die Masse ππβ . Dabei gilt πΈ = βπ; ππβ = β π Photonen besitzen keine Ruhemasse. ππβ = βπ π² Der Impuls ππβ des Photons ergibt sich aus der Definition π = ππ£ zu βπ βπ β ππβ = ππβ β π = π 2 β π = π bzw. mit π = π π folgt auch ππβ = π 1.1.5 Masse und Impuls des Photons Photonen haben die Energie E, den Impuls ππ·π und die Masse ππβ . Dabei gilt Fotoeffekt Einstein E=mc² πΈ = βπ; ππβ = β π Photonen besitzen keine Ruhemasse. ππβ = βπ π² Definition P=mv Einschub : Grundwissen zum Impuls in der Physik Folgerung : Wenn Photonen ein Impuls zugeordnet werden kann, dann können Photonen Stöße mit anderen Teilchen durchführen, die ähnlich den Stößen zwischen massiven Körpern, z.B. Billardkugeln, verlaufen. Der Satz von der Impulserhaltung gilt auch für Stöße von Photonen mit anderen Teilchen. • Beispiel Fotoeffekt : - Impuls des Photons wird fast vollständig auf den gesamten Festkörper der Fotozelle übertragen. - Wegen viel größerer Masse des Festkörpers findet kaum ein Energieübertrag statt (analog Medizinball, der von einem Tischtennisball getroffen wird) ο Energie des Photons geht fast vollständig auf das Fotoelektron über. http://www.physicsmasterclasses.org/exercises/bonn2/de/inhalt-3.2.2.html Compton-Effekt Versuchsbeschreibung : Die Intensität der an einem Plexiglasblock gestreuten Strahlung wird gemessen, wobei sich eine Aluminiumplatte als Absorber erst in der Stellung 1, dann in der Stellung 2 befindet. Ergebnis : Mit dem Absorber in Stellung 1 ist die Zählrate höher als mit dem Absorber in Stellung 2. Der Unterschied der Zählraten beträgt etwa 10%. Compton-Effekt • Impulsänderung von Photonen der Röntgenstrahlung beim Stoß mit Elektronen. • Je geringer die Energie der Röntgenstrahlung, desto höher die Absorption durch das Aluminium • Zusätzlich zur ursprünglicher Wellenlänge λ, der Streustrahlung, gibt es noch langwelligere Photonen mit Wellenlänge λ‘ Deutung : Beim Stoß von Photonen mit Elektronen werden wie bei einem elastischen Stoß Energie und Impuls übertragen. Daher enthält die gestreute Strahlung einen Anteil mit größerer Wellenlänge. Anmerkung : Eine genauere Untersuchung zeigt, dass die Wellenlängenänderung nicht größer sein kann als rund 5pm. Der Compton Effekt lässt sich deshalb nur bei kurzwelliger Strahlung (Röntgen oder Gammastrahlung) nachweisen. Beispiel Compton-Effekt Deutung : Beim Stoß von Photonen mit Elektronen werden wie bei einem elastischen Stoß Energie und Impuls übertragen. Daher enthält die gestreute Strahlung einen Anteil mit größerer Wellenlänge. Übung 13: Berechnen Sie den Impuls eines Photons aus dem Spektrum des sichtbaren Lichts (λ=600nm) und eines Röntgenphotons der Energie 30 keV. Lösung : • P(λ=600nm) = πΈ β π = 1,1 β 10−27 ππ . • P(E=30keV) = π = 1,6 β 10−23 ππ Übung 14: Ein Photon (λ=250nm) trifft senkrecht auf die Oberfläche einer Zinkplatte (πΈπ΄ =4,3eV) und löst dort ein Fotoelektron heraus. Dieses wird senkrecht zur Oberfläche emittiert. a) Berechnen Sie die Geschwindigkeit des Fotoelektrons und die Impulse von Photon ππβ und Elektron ππ . b) Erläutern Sie, inwiefern das Ergebnis (ππβ β« ππ ) mit dem Impulserhaltungssatz vereinbar ist. Lösung a) βπ Die Energie des Photons beträgt πΈπβ = π = 7,95 β 10−19 π½ = 5,0 ππ. Damit ergeben sich die Energie des Fotoelektrons und daraus dessen Geschwindigkeit und Impuls zu πΈπ = πΈπβ − πΈπ΄ = 5,00ππ − 4,5ππ = 0,70ππ. Aus πΈπ = 1 π π£ ² folgt π£π 2 π π = 2πΈπ ππ 1,4β1,60β10−19 π½ = 9,11β10−31ππ = 4,5 β 10−25 ππ . = 5,0 β 105 π π ππ = ππ β π£π β Der Impuls des Photons hingegen beträgt nur ππβ = π = 2,54 β 10−27 ππ . Lösung b) Das Fotoelektron nimmt nur die Energie des Photons auf, nicht dessen Impuls. Der Impuls des Photons und der bei der Emission des Fotoelektrons auftretende Rückstoß gehen auf die Zinkplatte über. Übung 15: Die Sonne bestrahlt die Erde mit 1,36 kW/m². Zeigen Sie, dass a) der Gesamtimpuls ππππ der pro Zeiteinheit eingestrahlten Photonen nur von der Strahlungsleistung P (und nicht von den vorkommenden Wellenlängen) ππ‘ abhängt : ππΊππ = π . b) der Impuls der Photonen, die pro Sekunde und Quadratmeter auf die Erde treffen, 4,5 β 10−6 ππ beträgt. c) Berechnen Sie, welche Kraft die Sonnenphotonen auf einen Spiegel mit der Fläche 1,0 m² ausüben, von dem sie senkrecht reflektiert werden. Lösung a) Lösung b) Lösung c)
